基于信息熵抑制的轨迹隐私保护方法
汪逸飞,罗永龙,俞庆英,刘晴晴,陈 文
(1.安徽师范大学 计算机与信息学院,安徽 芜湖 241003; 2.安徽师范大学 网络与信息安全安徽省重点实验室,安徽 芜湖 241003)(*通信作者电子邮箱wyf927@ahnu.edu.cn)
0 引言
近年来,随着智能设备的兴起和全球定位系统(Global Positioning System, GPS)等卫星导航技术的快速发展,人们越来越多地使用定位技术、路径推荐以及基于位置的社交网络等位置服务(Location Based Service, LBS)技术,由此产生了大量的移动轨迹数据。一方面,这些数据有利于研究者对其分析从而挖掘出有用价值;另一方面,这些轨迹数据里包含了大量的用户敏感信息,如果不经任何处理直接发布,会导致用户隐私的泄露。因此,数据发布者在发布数据时,既要保护用户的隐私信息,又要最大化地保证匿名数据的可用性。现如今用户的轨迹隐私保护问题已成为了研究者和用户重点关注的问题[1-3]。
目前,轨迹隐私保护技术主要集中于假数据法和泛化法,已取得大量研究成果[3],但传统的轨迹隐私保护法并不适用于高维轨迹数据的隐私保护。针对高维轨迹所体现出的高维性、稀疏性以及有序性等问题,国内外学者提出使用抑制法能较好地解决这个问题,轨迹抑制法是指在轨迹发布前去除某些敏感或频繁访问的位置。Terrovitis等[4]假设攻击者拥有部分真实轨迹,提出在轨迹发布时抑制处于敏感区域的位置,使轨迹泄露的风险不高于用户设置的隐私保护阈值,然而,如何找到合理的轨迹抑制位置从而减少抑制法带来的数据损失仍然是轨迹抑制隐私保护法有待解决的一个关键问题; Chen等[5]基于LK(Length K-anonymity)模型寻找出所有违反模型的轨迹序列的思想,并考虑到全局抑制轨迹序列会造成较大的数据损失,进一步提出局部轨迹抑制保护算法;Komishani等[6]考虑到敏感属性相似性攻击问题,提出了泛化敏感属性的隐私保护算法;赵婧等[7]基于轨迹频率,通过对有问题的轨迹添加假数据和利用隐私关联度和数据效用之间的关系对轨迹数据进行处理,提出了两种轨迹抑制的隐私保护方案;Ghasemzadeh等[8]基于概率流量图,通过全局与局部抑制对乘客流量进行隐私保护。然而,当前采用的抑制法依然存在不足:由于隐私保护方不能确切知道攻击者掌握的背景知识,仅通过抑制不满足设定阈值的实例,可能会增大攻击者识别某些敏感地区的概率;同时由于抑制操作的盲目性会造成大量的数据损失,影响高维轨迹数据的发布质量。
针对上述问题,本文在文献[8]的基础上,针对传统轨迹抑制法造成的较大数据损失的问题,提出了一种基于信息熵抑制的轨迹隐私保护算法(Trajectory Privacy-preserving algorithm based on Information Entropy, TP-IE)。本文主要工作如下:首先,对当前数据集建立基于熵的流量图,计算每一条路径中时空点的熵值;然后基于每个树节点的信息熵设计消除轨迹违反序列的花费代价函数,迭代选择序列进行抑制操作,实现轨迹的匿名发布;最后,重新设计了比较抑制前后流量图相似性的算法,提出了一个计算隐私收益的函数。通过详细的实验对比,证明了本文算法具有更高的应用价值。
1 相关定义
定义1 轨迹。轨迹是指移动对象的位置信息按照时间顺序排序得到的序列。通常情况下,轨迹可以表示为tr:(ID,(loc1t1→loc2t2→…→lociti)),其中ID为用户标识符,lociti被称作为tr轨迹的一个时空点,表示移动对象在ti时刻的位置为loci,|tr|为轨迹的长度,即轨迹中不同时空点的个数。用T={tr1,tr2,…,trn}表示由n条轨迹数据形成的轨迹数据集。
定义2 身份链接攻击[5]。身份链接攻击是指攻击者为获取用户的隐私信息,根据所掌握的部分用户信息和对应的用户身份信息发起的攻击。
定义3 LK模型[5]。假设L为背景知识的最大长度,即攻击者掌握用户轨迹序列包含的最多时空点个数,满足LK模型的序列q需要满足下列条件:
1)|T(q)|≥K,其中T(q)表示轨迹包含q, |T(q)|表示包含q的轨迹条数,其条数至少为K条;
2) 0<|q|≤L,|q|表示序列q包含的轨迹时空点个数,至多为L个。
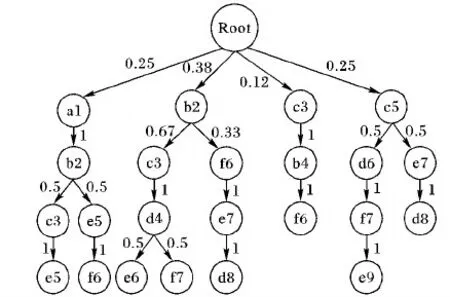
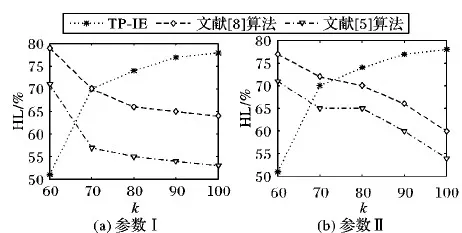
定义4 违规序列[5]。假设q为轨迹数据集中的轨迹序列且长度满足0<|q|≤L,当且仅当|T(q)| 定义5 最小违规序列[5]。假设q为违规序列,q的所有可能子序列都不是违规序列,则称q为最小违规子序列(Minimal Violating Sequence, MVS)。 定义6 基于熵的流量图。基于熵的流量图是指由一系列时空点组成的有向图,它采用树作为存储结构,可表示为三元组ET=〈G,PATH,Root(ET)〉,其中G表示该流量图节点的集合,PATH表示该流量图路径的集合,Root(ET)表示流量图的根节点。 在基于熵的流量图中,图的路径集合PATH可用{Path1,Path2,…,Pathi,…,Pathn}表示,其中Pathi表示流量图中的第i条路径;每个节点(除了根节点)只有唯一的父亲节点,对于除根节点外的任意节点d∈G,可用d=〈location,time,ent,count,children〉表示,其中location代表该节点的位置,time代表该节点的时间,ent代表该节点的时空点熵(如定义7所述),count表示该节点的孩子节点的分支数,children代表该节点的孩子节点。 定义7 时空点熵。时空点熵是指时空点信息量的大小。对于除根节点外的任意节点d∈G,假设d的上一个节点转移到当前节点的概率为p,时空点熵H(d)为: H(d)=-plgp (1) 表1列举了8位乘客的轨迹路径,其中每条轨迹由一系列的时空点组成。每个时空点的形式为(lociti),表示乘客在ti时刻的位置为loci。例如:“a1”表示在1时刻处于位置“a”,“c3”表示在3时刻处于位置“c”。 表1 原始轨迹数据集示例 根据表1中乘客的原始轨迹集,可以建立如图1所示的乘客概率流量图。转移概率p(dx→dy)表示由dx移动到dy的乘客比例,如图1所示,50%的乘客在经过a1和b2后前往e5。 图1 基于熵的流量图 传统的轨迹抑制法通过假设攻击者的背景知识,抑制不满足于设定阈值的时空点或轨迹序列以达到隐私保护的目的。文献[5]通过假设攻击者最大的背景知识,建立如定义3所示的LK模型,枚举出轨迹数据中所有违反模型的违规序列,然后构建合理的花费代价函数计算抑制违规序列的代价,局部抑制时空点以达到隐私保护的目的。文献[8]针对乘客客流分析问题,在文献[5]的基础上,通过建立乘客流量图重新设计消除违规序列的花费代价函数,以达到保护乘客隐私的同时最大化地保证客流分析的信息质量的目的。然而上述方案依然存在以下问题:1)采用抑制法对违规序列处理时,没有考虑时空点之间的转移概率,通往下一个时空点转移概率值较高或波动较大的时空点,对用户的隐私威胁更加严重,应当优先处理;2)在处理违规序列时,由于仅仅考虑了时空点数量对隐私保护的影响,导致限制发布的数据较多,增加了数据损失。 针对上述问题,本文基于LK模型,结合信息熵度量的思想提出了基于信息熵的轨迹抑制法。 信息熵是1948年Shannon[9]借鉴热力学概念,提出的衡量信息量大小(信息不确定度)的概念,解决了对信息的量化度量问题。 信息熵常常用于表示某种特定信息的出现概率,一个系统越是有序,信息熵就越低;反之,一个系统越是混乱,信息熵就越高。文献[10]通过建立基于信息熵的无向图来度量轨迹隐私,攻击者对用户轨迹隐私攻击的主要目的是要挑选出用户出行概率最大的轨迹:如果攻击者认为特定用户每条可能的运动轨迹的概率相等,那么系统越混乱,攻击者难以攻击;如果每条可能的运动轨迹的概率差别很大,那么表示系统越有序,则易遭受到攻击,因此,在基于熵流量图里,抑制法在选取合理的抑制位置时,应当尽可能保留信息熵值大的树节点,一方面可以减少信息损失,另一方面增加了抑制后数据的隐私保护性。 本文提出了一种基于信息熵的轨迹抑制隐私保护算法(TP-IE)。TP-IE是基于文献[5]提出的LK模型重新设计的隐私保护算法,其算法设计的主要思路为:首先,对轨迹数据建立了如图1所示的基于信息熵的流量图,利用熵值来衡量轨迹时空点的信息量;其次,基于LK模型枚举出轨迹数据中的敏感位置点,即最小违规序列,结合信息熵建立合适的花费代价函数(定义9),通过函数计算抑制敏感位置点的最低代价;最后,选取合理的抑制方式(局部抑制或全局抑制)对原始数据集中包含敏感点的序列进行抑制,直到轨迹数据集中的所有序列均满足LK模型。TP-IE不同于以往的轨迹匿名方法,其优点主要在于:1)结合信息熵值对时空点进行度量,有效地考虑到了时空点转移概率的变化,对于某些转移概率相差较大即熵值较低的点加以抑制,并在抑制过程中最大化保留熵值较大的点;2)TP-IE是通过求解隐私收益与数据实用性之间的关系来对轨迹数据进行抑制。在每次进行抑制的过程中,由于抑制的时空点都是利用花费代价函数计算出的最优解,从而增加了匿名处理后的数据实用性和隐私收益。为了验证算法的实用性,本文基于抑制前后的时空点熵的变化,设计了一个比较熵的流量图的相似性算法来衡量经过抑制处理后数据集的实用性。 LK模型枚举出最小违规序列,通过抑制最小违规序列达到轨迹隐私保护的目的[5]。为了减小序列抑制带来的信息损失,考虑到各序列q的实用价值,本文通过建立基于信息熵的流量图重新设计了消除q的花费代价函数。 定义8 Info值。Info(d)是用来衡量时空点d在轨迹数据集以及流量图中的信息质量的值,Info(d)定义为: Info(d)=(Hα(d)×α(d)+Hβ(d)×β(d))×γ(d) (2) 其中:α(d)表示流量图中相同节点d的数目之和,β(d)表示d在流量图里的孩子节点分支数目之和,γ(d)表示原始数据集里含有d的路径数之和,Hα(d)表示d在流量图里的相同节点的时空点熵值和,Hβ(d)表示d点的孩子节点时空点熵值和。 示例1 如图1所示,α(b2)=3因为流量图里有3个b2的节点,β(b2)=5因为流量图里的b2节点共有5个分支,γ(b2)=6因为原始数据集T里有6条包含b2的路径,由式(1)可得出Hα(b2)=0.15,Hβ(b2)=0.56,则可由式(2)得出Info(b2)的值。 定义9 Score值。根据d的抑制方式,定义一种花费代价函数来计算消除d时空点的花费代价,如式(3)所示: Score(d)=PrivGain(d)/Info(d) (3) 其中PrivGain(d)表示消除d后MVS减少的个数。 TP-IE主要分为两部分:第1部分在原始轨迹数据集上生成轨迹流量图,遍历流量图中每个时空点,计算每个时空点的Info值,如算法1所述;第2部分获取轨迹数据集中的最小违规序列并对最小违规序列进行时序抑制序列方式判断,选取局部抑制或全局抑制对其抑制处理,如算法2所述。 算法1首先通过原始数据集T生成基于熵的流量图ET;然后遍历熵的流量图中的每个节点,如果流量图中存在时间、位置相同的时空点,分别计算它们的α(d)、β(d)、Hα(d)、Hβ(d)(第1)~11)行);接着统计流量图里包含时空点d的路径数,计算出γ(d)(第12)~16)行);根据上述值计算出每个时空节点的Info(d),返回Info值(第17)~19)行)。 算法1 计算每个时空点的Info值—— GetInfo。 输入 原始轨迹集T; 输出 时空点的信息质量Info。 1) Generate flowgraphETfrom databaseT; 2) for eachdinGdo 3) α(d),β(d),γ(d),Hα(d),Hβ(d)均初始化为0; 4) for eachd′ inGdo 5) ifd.location==d′.location&&d.time==d′.timethen 6) α(d)←α(d)+1; 7) Hα(d)←Hα(d)+d′.ent; 8) β(d)←β(d)+d′.count; 9) Hβ(d)←Hβ(d)+d′.children.ent; /*孩子节点的时空点熵之和*/ 10) end if 11) end for 12) for eachpathinPathdo 13) ifpathcontainsdthen //如果路径中包含d 14) γ(d)←γ(d)+1; 15) end if 16) end for 17) Info(d)=(Hα(d)×α(d)+Hβ(d)×β(d))×γ(d); 18) end for 19) return Info 算法2是序列抑制阶段,首先调用文献[5]提出的MVS算法生成最小违规序列,然后根据算法1调用每个节点的Info值,由定义9建立出MVS的得分表(Score_table)(第1)~9)行)。接着,迭代选择得分表中最高分的时空点p(第10)~11)行),根据时空点p抑制方式的不同采取不同的操作:如果抑制方式是局部抑制,则将包含p的MVS放入到集合V′中,循环从V′中选取序列m,在轨迹数据集T中对所有包含m的实例抑制其中的时空点p(第12)~14)行);如果抑制方式是全局抑制,则删除轨迹数据集中的所有的时空点p(15~18行)。最后更新MVS和 Score_table中的所有时空点得分并检查各时空点的抑制方式是否发生改变;重复上述操作,直到Score_table为空(第19)~22)行)。 如表1所示,假设K=2,L=2时,{c3 → e5,b2 → e6,e9}为表中的MVS序列集合的一部分。本文抑制目的为消除原始轨迹数据集中的所有MVS;故通过定义9算出所有MVS的得分值,降序排列。假设c3为得分值最高的时空点,则在原始轨迹数据集中寻找所有包含c3的轨迹实例,采取全局抑制或者局部抑制的方式[5]抑制时空点c3,直到原始数据集里不存在包含c3的MVS序列;迭代进行直到MVS序列集合为空集。 算法2 对MVS序列进行抑制处理—— Sequence-suppression。 输入 原始数据集T,阈值L,K; 输出 满足LK模型的轨迹数据集T′。 1) GenerateMVS(T) by MVS algorithm; 2) GenerateInfo(T) by GetInfo algorithm; 3) for eachdinGdo 4) for eachpinMVS(T) do 5) ifd.location==p.location&&d.time==p.time 6) BuildScore_tablein descending order based on Eq.(3); 7) end if 8) end for 9) end for 10) whileScore_table≠∅ do 11) select a spatio-temporal pointpwith the highest score fromScore_table; 12) ifpis a local suppression point then 13) V′←{m′|m′∈MVS,p∈m∧T(m′)=T(m)}; 14) Suppress the instances ofdinT(m); 15) else 16) V′←MVS(p); 17) Suppress all instances ofpinT; 18) end if 19) Update theScore_table; 20) MVS←MVS-V′; 21) end while 22) T′←the suppressedT 轨迹数据经过匿名处理后,轨迹数目会减少,同时由于转移概率的变化,轨迹流量图会发生改变。文献[8]设计了比较匿名前后流量图变化的算法,但并未将转移概率的变化考虑在内。为了评测经过抑制法处理后的轨迹数据集的数据实用性,本文在文献[8]的基础上重新设计了流量图比较算法,其目的是为了验证抑制前后流量图结构未发生明显变化且轨迹数据挖掘性没有明显降低。 首先,匿名前后流量图中的所有节点都是按照时间、地点排序,然后按次序提取G与G′中的时空点d与d′(第1)~3)行):如果d与d′的时间、位置均相等,那么d与d′视作相同节点,并计算出它们的aSum、bSum、cSum、vSum、wSum、uSum(第5)~14)行);如果β(d)=0,即d为流量图里的叶子节点的值,由于β(d)为计算bSum时的分母,所以算法跳过此次除法,并使用i对β(d)=0计数(第11)~16)行),最后在计算相似性时流量图应减去叶子节点的数值(第22)行);接下来对vSum,uSum,wSum进行归一化记作svSum、suSum、swSum(第17)~21)行),最后第23)行返回相似性φ的值。 算法3 流量图比较——ComFlowgraph。 输入 轨迹流量图ET,匿名后流量图ET′; 输出 匿名前后轨迹相似性φ。 1) G←{d|d∈ET}; 2) G′←{d|d∈ET′}; 3) SelectGandG′ based on time and location; 4) i←0; 5) for eachd∈Gdo 6) for eachd′∈G′ do 7) ifd=d′ then 8) vSum←vSum+[Hα(d′)/Hα(d)]; 9) wSum←wSum+[Hϑ(d′)/Hϑ(d)]; /*根节点到当前节点的时空点熵和*/ 10) aSum←aSum+[α′(d)/α(d)]; 11) cSum←cSum+[γ′(d)/γ(d)]; 12) ifβ(d)≠0 then 13) bSum←bSum+[β′(d)/β(d)]; 14) uSum←uSum+[Hβ(d′)/Hβ(d)]; 15) else 16) i←i+1; 17) end if 18) end if 19) vSum,uSum,wSum归一化为svSum,suSum,swSum; /*归一化*/ 20) end for 21) end for 23) returnφ TP-IE首先生成轨迹流量图,计算各节点的时空点熵;然后基于LK模型生成MVS序列,计算每个时空点Score值,这部分最好情况下的时间复杂度为O(|s|2),最坏的情况下的时间复杂度为O(|s|2|T|),其中|s|为轨迹数据集的时空点个数,|T|为轨迹数据集路径数;最后序列抑制阶段会为每个MVS序列的消除都扫描一次数据集,所以其最好和最坏的情况下时间复杂度均为O(|s|2|T|)[5],因此,TP-IE算法最好情况下的时间复杂度为O(|s|2),最差情况下的时间复杂度为O(|s|2|T|)。第2部分比较流量图相似性,时间复杂度为O(|s|2)。 2.5.1 LK隐私模型有效 由于攻击者掌握用户的部分信息和对应的用户身份信息,所以攻击者可以根据这些局部信息发起身份链接攻击,进而推断出用户的身份。文献[5]指出传统k匿名模型针对高维轨迹数据的隐私保护需花费极大代价,因此高维轨迹隐私保护模型需要限定攻击者的背景知识不超过L,由定义3可知,LK模型可保证用户在受到身份链接攻击时被成功识别的概率≤1/k,故LK模型有效。 2.5.2 TP-IE实用性分析 TP-IE经过对原始流量图进行隐私保护处理后,流量图中节点的转移概率会发生变化[8]。式(2)结合信息熵值测量流量图中节点的信息质量,式(3)定义的花费代价函数实际上是通过求出实例损失与信息质量的最优解来抑制时空点。经过每一次迭代处理,信息质量较低且在原始轨迹中实例较少的时空点得到抑制;信息质量较大且包含实例数多的时空点得以保留,从而在提高隐私收益的同时减少了抑制法带来的数据损失。 定义10 数据损失率(Utility Loss, UL)。数据损失率是指原始数据集经过抑制处理后信息损失的值,记作UL。原始轨迹集的轨迹数目记作|T|,匿名后的轨迹集数目为|T′|,则数据集损失率UL计算公式为: (4) 传统抑制法用损失率来衡量信息损失,但单一的损失率只考虑到数据发布前后轨迹数目的变化,未曾考虑到抑制前后轨迹数据集信息增益的变化。本文基于文献[10]提出的位置隐私度量方法,通过信息熵变化重新定义信息损失值。 定义11 隐私收益。隐私收益是指原始数据经过匿名处理后增加的信息复杂度,记为HL。原始流量图里的节点熵值和记为|V|,匿名后的流量图节点熵值和记为|V′|,则隐私收益HL的计算公式为: (5) 实验硬件环境为CPU为Core i5-6500 CPU 3.20 GHz处理器、8 GB内存。本文使用C#语言在Microsoft Windows 10平台上进行实验模拟。本文采用的是一个模拟地铁交通运输系统的数据集Metro200k[8],拥有20万乘客在24 h内行驶于29个车站所形成的200 000万条轨迹记录,数据集大小为12 359 KB。 该数据集中每行数据包含用户身份及一段时间内的用户出行轨迹,经过对原始轨迹的处理,将原始数据转化为时间戳形式的轨迹序列,具体格式如表1所示。 高维轨迹隐私保护一般用隐私保护度和数据损失率来评价算法效率。本节将TP-IE同文献[5]和文献[8]提出的算法进行比较。文献[8]通过设置不同参数来测试算法的实用性,本文选取文献[8]实验效果最好的两组参数。后文实验图中A、B组分别包含文献[8]取两组参数时的实验效果。其中A组为wα=wβ=wγ=wδ=0.25,记作参数Ⅰ;B组参数wα=0.5,wβ=0.3,wγ=0.2,wδ=0,记作参数Ⅱ,其中wα,wβ,wγ,wδ表示不同的权值。 4.2.1 相似性 图2展示参数k对匿名后流量图的相似性影响。流量图相似性变化主要取决于两点:1)抑制轨迹时空点的数量;2)时空点熵值变化。当k=60时,TP-IE匿名后的流量图相似性明显高于文献[5]和文献[8]提出的两种方法。随着k值增加,轨迹抑制法抑制处理的数据点越多,流量图相似性降低;当k值增加到一定值时,算法将执行更多的全局抑制,因此相似性在逐渐达到平衡值会急剧下降。与文献[5]与文献[8]相比,由于时空点熵值较大的点保留更多,数据集的实用性也会更大。如图2所示,TP-IE在相同的匿名参数取值下相似性始终比另外两种方式高,所提方法在相似性度量上比文献[5]提出的方法提高了约27%, 比文献[8]方法提高了约22%。由此可以说明TP-IE使得抑制处理后的流量图相似性优于文献[8]和文献[5]提出的两种方法。 图2 k对匿名后流量图的相似性影响(L=3) 4.2.2 数据损失率 图3展示了参数k对数据损失的影响情况。数据损失主要受到抑制时空点数量变化的影响。随着k值增大,抑制的时空点越多,原始数据集的数据损失率越大。对比三个不同算法发现:随着k值增大,TP-IE的数据损失率始终最低,当k值增长到一定程度时,本文算法的数据损失率趋于稳定,但文献[5]与文献[8]仍有较大的增长。经过计算可得,在相同匿名参数的影响下,TP-IE比文献[5]算法在数据损失量上降低了约25%,比文献[8]算法降低了约21%。因此可以得出结论本文提出的算法可以最大化地减小抑制法带来的数据损失。 图3 k对数据损失的影响(L=3) 4.2.3 隐私收益 本文通过匿名前后的熵值变化来计算算法带来的隐私收益。图4展示了k值对于隐私收益的影响,可以看出文献[5]与文献[8]算法在k值较小时隐私收益均高于本文算法,这是由于当k值较小时,匿名算法执行的更多是局部抑制,文献[8]与文献[5]算法在隐私需求较低、数据损失较小的情况下,能带来更高的隐私收益;然而,随着k值逐渐增大,隐私需求提升时,匿名算法更多的执行全局抑制。TP-IE在执行抑制的过程中实则消除了流量图中熵值较低的点,保留了熵值较大的点,同时由于轨迹数据集中实例数量较低和转移概率较小的点得以抑制,实际上增大了原先熵值较低的时空点,因此,TP-IE匿名后的流量图的隐私收益会呈现出较大的增长;而文献[5]与文献[8]算法随着k值的增大,数据损失会越来越大,在抑制的过程中将会舍弃大量熵值较高的时空点,降低了原始轨迹的数据实用性,也使得隐私收益出现明显下降。经过计算可以得出在相同匿名参数取值下,TP-IE在隐私收益上比文献[5]算法提高了约21%,比文献[8]算法提高了约11%。因此,当k值持续增长时,本文方法会带来更高的隐私收益,在实用性上明显高于其余二者。 图4 k值对于隐私收益的影响(L=3) 本文基于LK模型提出了一种基于信息熵抑制的轨迹隐私保护方法,对原始轨迹集建立基于信息熵的流量图,根据图节点的熵值大小局部抑制违反模型的时空点,进而实现抑制敏感点的同时最大化保留轨迹数据实用性的目的。在仿真数据集上的实验表明,本文方法在匿名前后流量图的相似性、数据损失率以及隐私收益三个方面均优于文献[5]与文献[8]提出的算法,证明了TP-IE的有效性和实用性。本文算法前提是假设攻击者的背景知识长度不超过L,然而现实生活中攻击者的背景知识大部分是未知的,如何在不知晓攻击者背景知识的条件下达到保护用户隐私的目的是下一阶段主要研究的问题。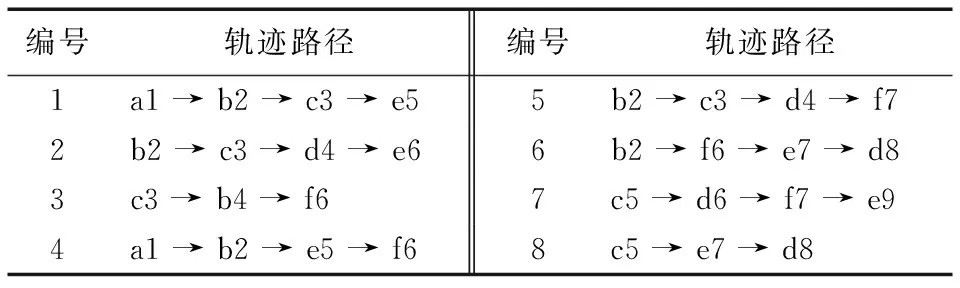
2 基于信息熵抑制的轨迹隐私保护方法
2.1 信息熵
2.2 隐私保护算法—— TP-IE
2.3 数据实用性比较
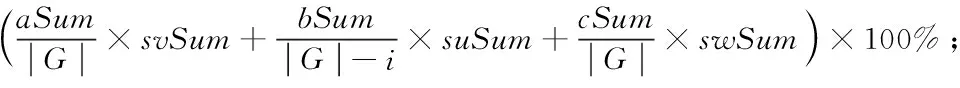
2.4 TP-IE时间复杂度
2.5 TP-IE安全性分析
3 衡量标准
4 实验与分析
4.1 实验环境及数据集
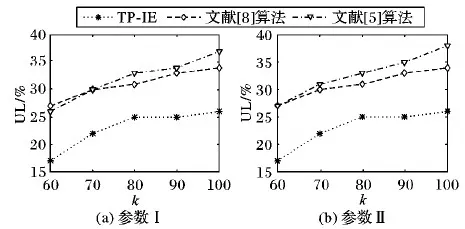
4.2 实验结果分析

5 结语

