基于极端学习机的人脸特征深度稀疏自编码方法

张欢欢，洪 敏，袁玉波

(华东理工大学 信息科学与工程学院, 上海 200237)(*通信作者电子邮箱ybyuan@ecust.edu.cn)

0 引言

近年来，随着电子移动设备的普及，生物特征识别技术已经被广泛应用于工业各个领域，其中人脸识别技术[1-2]以其易于接受和采集方便的特点成为身份识别的重要组成部分，在视频监控系统、银行支付验证、智能门禁系统等实际应用中有着显著的优势，成为了目前身份识别的主流技术之一; 然而，人脸图像样本数据维度比较高并且混杂大量噪声的特点极大地制约了人脸识别的准确率，因此从人脸图像中提取有效人脸特征成为了人脸识别的重要问题。

基于自编码器(Auto-Encoder, AE)的深度神经网络结构可以对人脸特征进行高层次的抽象表示，利用重构的思想，逐步提取样本的低维或高维特征，具有极强的特征表达能力，在人脸图像混杂噪声或受误差干扰的情况下可以提取到重要的人脸特征。由于传统的自编码器模型[3-4]大部分采用反向传播(Back Propagation, BP)算法，模型的收敛速度缓慢，需要大量的参数进行微调，且易陷入局部最优。而极端学习机(Extreme Learning Machine, ELM)算法不需要使用传统的BP算法对网络进行微调，只需人工设置隐含层节点数即可实现网络功能，减少了训练网络的成本。许多专家学者提出了很多关于ELM的变型算法[5]，但其单隐层结构具有局限性，导致其无法学习到有效的特征。2013年，Huang等[6]第一次将极端学习机与自动编码器结合，提出基于极端学习机自编码器(Extreme Learning Machine Auto-Encoder, ELM-AE)的多层极端学习机(Multi-layer Extreme Learning Machine based Auto-encoder, MLELM)算法，它是一种无监督学习算法，将随机生成的隐含层输入权值和偏置参数正交化，并将原始数据空间映射到不同维度的特征空间，从而实现不同维度的特征表达。此外，还有许多基于ELM-AE的多层模型[7-9]研究，通过增加隐含层数量构成深度学习模型，提取样本更本质的特征。

随着稀疏表示[10]和压缩感知理论[11]的发展，稀疏表示被用于人脸识别领域并取得了较好的识别效果，众多研究者提出了许多基于人脸特征的稀疏表示方法[12-14]，从特征层面入手，将人脸识别看作是人脸图像的稀疏特征表示问题。2015年,Hu等[15]提出了一种基于截断式核范数正则化(Truncated Nuclear Norm Regularization, TNNR)[16]的可扩展的大规模多分类算法，虽然TNNR的提出主要用于图像修复以及低秩矩阵补全，但是矩阵补全问题的核心在于获取矩阵的未知低秩结构，即求解秩最小化的优化问题，从而得到输入图像的稀疏表示。此外，为了高效求解此类凸优化子问题，Zhang等[16]还提出基于加速的最近邻梯度线性搜索算法(Accelerated Proximal Gradient Line Search, APGL)的截断式核范数优化算法(TNNR-APGL)。只要输入的数据矩阵的确存在低秩结构，通过求解最小化截断式核范数问题一定可以得到最优的低秩解，输入矩阵的低秩结构就可以被更好地估计。

对于人脸特征较少的图像，MLELM算法相当有效，但该算法误差模型的计算方式存在缺陷，没有考虑数据内在的结构，当人脸特征较多时会出现识别率降低的问题。为了解决高维人脸图像的识别率降低的问题，提高模型对于噪声数据的抗干扰能力，本文提出了一种新的方法来解决该问题。该方法的基础是加入截断式核范数正则化的误差模型，通过最小化误差模型得到人脸图像映射到新空间的低秩结构；然后利用极端学习机进行人脸特征的自编码，获取人脸特征的稀疏表示；最后得到人脸图像的识别结果。从文中的给出的实验结果可看出，本文方法非常有效。

1 基于极端学习机的深度稀疏自编码器

本章首先介绍了基于极端学习机的稀疏自编码器模型，将截断式核范数正则化理论与ELM-AE相结合，提出了稀疏自编码器(Sparse Auto-Encoder based on Extreme Learning Machine, ELM-SAE)的方法； 然后利用深度学习的思想，将多个稀疏自编码器栈式叠加构成深度稀疏自编码器(Deep Sparse Auto-Encoder, DSAE)模型。

1.1 稀疏自编码器

如图1所示，ELM-SAE的网络结构是与ELM-AE相同的三层神经网络。它是一种无监督学习算法，其输出与输入一致，具备极端学习机输入参数随机赋值、无需迭代优化等优点，在尽可能复现输入人脸图像的同时，对人脸特征执行自动编码，从而得到人脸稀疏特征作为模型输出。

图1 ELM-SAE网络结构

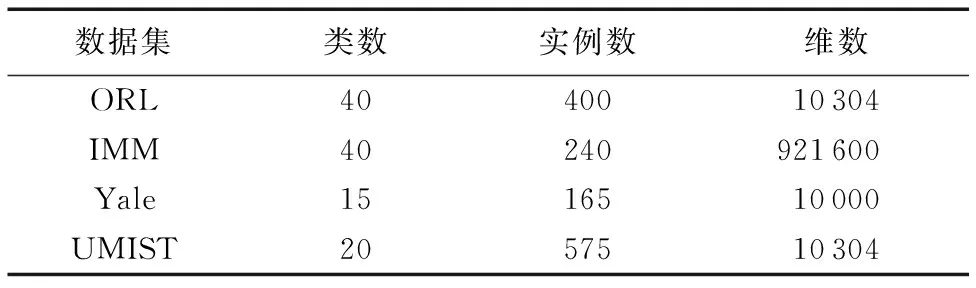
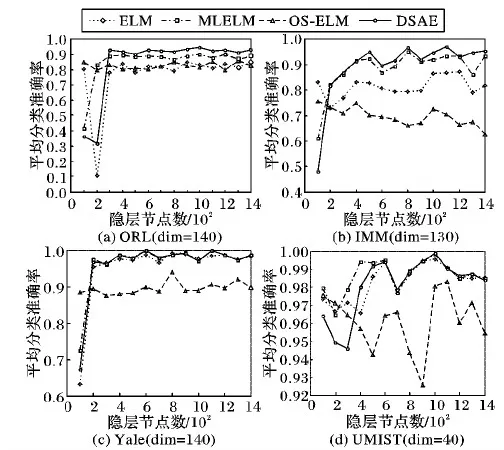
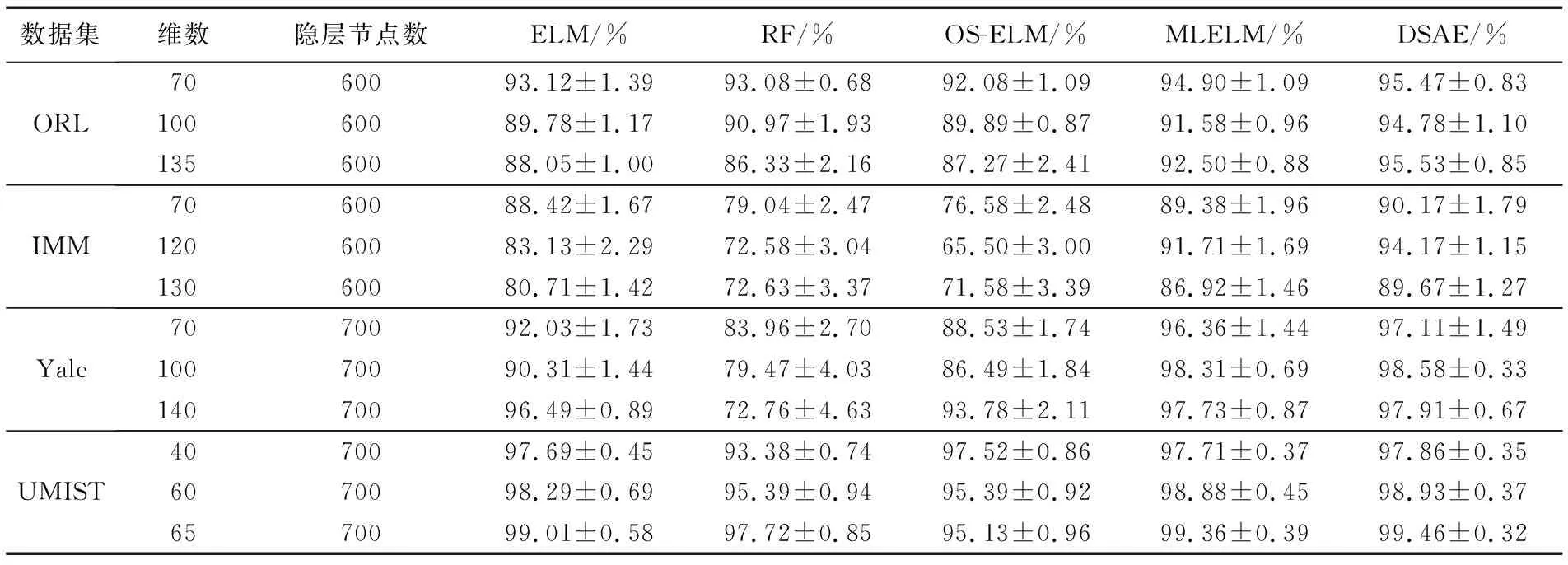
假设ELM-SAE具有j个输入层节点、L个隐含层节点和j个输出层节点，隐含层上的激活函数是g(x)，根据输入人脸特征的隐层输出可以将ELM-SAE分为如下三种情况：若j>L，压缩表示，将特征向量从高维空间映射到低维度特征空间；若j=L，等维表示，实现等维度特征映射；若j

ELM-AE的损失函数如下

(1)

其中:X= [x1T,x2T,…,xNT]T∈RN×j，β为输出权值向量，H= [h(x1)T,h(x2)T,…,h(xN)T]T∈RN×L，C为训练误差的惩罚因子。因此ELM-AE的输出权值向量β可由式(2)计算得到：

(2)

ELM-AE使用的最小化核范数问题并不能保证输出矩阵具有低秩结构，其弊端在于所有的奇异值被同时要求最小化，导致核范数奇异值惩罚不平衡的问题，原始矩阵的秩不能很好地被估计。由于矩阵的大奇异值决定矩阵的主要性质，因此在设计低秩惩罚项时，需要对矩阵大的奇异值惩罚力度减小，小的奇异值惩罚力度加大。ELM-SAE与ELM-AE最大的不同之处在于输出权值的计算方式不同：ELM-AE通过最小化最小二乘估计的损失函数求得，ELM-SAE在此基础上加入截断式核范数正则化项对损失函数进行约束，只惩罚值较小的奇异值，避免对较大奇异值的惩罚，即当输入矩阵的秩为r时，其最大的r个非零奇异值并不能影响矩阵的秩，影响较大的反而是较小的奇异值。

根据文献[15]分析，给定矩阵X∈RN×j,假设UΣV是X的奇异值分解，参数r≤min(m,n)，Σ∈RN×j，U=(u1,u2,…,uN)∈RN×N，V=(v1,v2,…,vj)∈Rj×j，则截断式核范数与传统核范数之间存在的联系为：

(3)

其中:Ur=(u1,u2,…,ur)T∈Rr×N,Vr=(v1,v2,…,vr)T∈Rr×j。即等价于以下优化问题

(4)

λ(‖W‖*-Tr(UrWVrT))

(5)

其中第一项和第二项的含义与ELM-AE相同；然后利用编码结果的核范数和秩截断项构成了惩罚函数，其中λ为惩罚因子，W为输入矩阵X的低秩矩阵，Ur和Vr为X的奇异值向量。

显然式(5)是无法直接求解的凸问题，因此需要设计有效的迭代机制对输出权值向量进行求解。上述最优化问题的最小化损失函数(5)形如:

(6)

其中:g(·)为封闭的、可能不可微的凸函数,f(·)为可微的凸函数，因此本文采用TNNR-APGL优化算法对最小化损失函数进行求解。令:

(7)

根据文献[11]中定义4.1，在第k次迭代中，给定矩阵Yk+1和参数tk+1>0。式(8)推导出Wk+1的值。Yk+1和tk+1以相同的方式更新，见式(11)～(12):

λDλtk(Yk+tk(λUrTVr+μX-μYk))

(8)

(9)

(10)

通过对式(5)的求解，则可得到输出权值β为:

(11)

其中βTβ=I，W为输入矩阵X的低秩矩阵。综上所述，ELM-SAE首先随机生成输入层与隐含层之间的输入权值和隐含层上的偏置并正交化, 将输入人脸图像映射到不同维度的特征空间，然后计算隐含层的输出矩阵，最后计算隐含层与输出层之间的输出权值实现人脸特征的重新表述。

1.2 深度稀疏自编码器

本节主要介绍基于极端学习机的深度稀疏自编码器(DSAE)模型，其网络结构如图2所示。

图2 DSAE模型网络结构

DSAE利用无监督学习算法ELM-SAE对各层参数进行训练，将ELM-SAE作为基本学习单元，执行逐层无监督学习。首先用ELM-SAE训练第一层网络，得到第一层隐含层的输出，再将其作为第二层输入训练第二层网络，以此类推，第k个隐层的输出和第(k-1)个隐层上的输出的数值关系由式(12)表示:

Hk=g((βk)THk-1)

(12)

其中：Hk表示第k个隐含层的输出，当k=1时，Hk-1表示输入层的输出，βi表示ELM-SAE对第(k-1)个隐层和第k个隐层训练时的权值矩阵。DSAE上的输出权值β通过式(11)求得。

与其他深度模型相同的是，DSAE也使用无监督学习算法对各层参数进行训练，但不同之处是DSAE不需要对网络参数反复迭代调整，对网络模型的训练速度快。

2 算法设计

本章首先介绍使用TNNR-APGL优化算法对ELM-SAE模型的最小化损失函数进行迭代求解的过程，然后介绍了人脸特征DSAE分类算法的具体步骤。

2.1 基于TNNR-APGL的迭代算法

求解最小化截断式核范数问题并不是一个凸优化问题，本文采用TNNR-APGL算法对其迭代求解，首先固定其中一部分变量，得到剩余变量的封闭解；然后继续固定剩余变量，通过求解凸优化子问题更新之前固定的变量，交替执行这两个过程，就可以得到该凸优化子问题的解。由于TNNR-APGL算法更适合处理带噪声的图像，因此本文选用此优化算法。

算法1 基于TNNR-APGL的迭代算法

输入 人脸特征矩阵X，X的奇异值向量Ur和Vr，误差参数ε，惩罚项系数λ和μ;

输出 输入矩阵X的低秩矩阵W。

1) TNNR_APGL(Ur,Vr,X,λ,μ,ε)；

2) Repeat

3) 首先固定Yk和tk，式(8)更新Wk+1；

4) 固定Wk+1和Yk，式(10)更新tk+1；

5) 最后固定Wk+1和tk+1，式(9)更新Yk+1；

6) Until ‖Wk+1-Wk‖F≤ε

算法1是对式(5)中最小化损失函数进行迭代求解的过程，输入为人脸特征数据，输出为人脸稀疏特征数据，不断循环执行步骤3)～5)，直到输出误差小于误差参数则终止循环。由传统APGL的收敛性质得知，该迭代算法的收敛速度为O(1/n2)，其中n是迭代的次数。

2.2 人脸特征DSAE分类算法

算法2是人脸特征DSAE分类算法的具体步骤，输入为人脸图像数据集，首先对原始人脸图像进行预处理，将所有人脸图像样本处理为一个人脸数据矩阵，再使用主成分分析(Principle Component Analysis, PCA)对人脸数据矩阵进行压缩降维处理，提取人脸数据中相对重要的特征即人脸特征数据作为DSAE模型的输入;然后对DSAE神经网络结果进行初始化，选取合适的隐层节点数、模型深度以及初始化参数，将人脸特征数据按照2 ∶1的比例划分为训练集和测试集。使用训练集对模型进行训练，每层进行训练的过程都是对人脸特征数据进行不断提取和再表示的过程，输出人脸稀疏特征再进行下一层的训练; 最后使用该模型在测试集上验证分类算法的准确率，并计算循环s次算法的平均准确率。

算法2 人脸特征DSAE分类算法。

输入 人脸特征数据集D={xi∈Rj,yi}(i=1,2,…,N)，无标签的训练次数s，激活函数g(x)，隐含层个数k，惩罚项系数λ和μ，隐含层节点数nhl(l=1,2,…,k)。

输出 测试集s次分类结果的平均值。

1) 使用PCA对人脸特征数据集D进行预处理；

2) 初始化DSAE神经网络，将样本分为训练集Xtrain和测试集样本Xtest，X1=Xtrain；

3) forl=1:k

4) 随机产生ELM-SAE第l层的输入权值ai和偏置bi；

5) 计算第l层的输出权值βl；

6) 计算输出Xl+1=g(XlβlT)；

7) end for

8) 使用输出权值β计算测试集Xtest的分类准确度，以上过程循环s次，计算分类结果的平均值

3 实验与结果

为了证明本文算法的有效性，本文使用人脸数据集将本文提出的DSAE算法与经典的随机森林(Random Forest, RF)算法以及ELM、在线序列极端学习机(Online Squential Extreme Learning Machine, OS-ELM)和MLELM算法的分类效果进行比较(均采用Sigmoid激活函数)。以上几种方法都是在Intel Core i5-2450M CPU 2.5 GHz处理器、8 GB内存、Windows10 64位操作系统和Matlab 2016a的环境中运行的。

3.1 数据集

本文将在ORL、IMM、Yale和UMIST 4个人脸数据集上测试本文所提方法。选取人脸数据集中每人的2/3张图片作为训练样本，剩下的1/3张图片作为测试样本来进行实验，每个实验分别重复30次以获取一个较为准确的识别率。实验中使用的人脸数据集描述的详细信息见表1。不同人脸库的训练集如图3所示。

表1 实验中使用的人脸数据集

图3 人脸数据集

3.2 实验和结果分析

本节主要对比了DSAE与ELM、RF、OS-ELM、MLELM分类算法的性能。为了实验的公平性，本文中的惩罚参数值大小相同，ELM、OS-ELM的隐层节点数与MLELM、DSAE的第一层隐层节点数相同，MLELM与DSAE的隐层层数相同。对每个数据集，通过比较分类准确率确定隐层节点个数和样本维数。

图4给出了ELM、RF、OS-ELM、MLELM和DSAE在ORL、IMM、Yale和UMIST数据集上随着样本维数的改变，五种算法的分类准确率的变化情况, 其中X轴表示样本维数，Y轴表示30次实验的平均分类准确率。

图4(a)为五种分类算法在ORL人脸数据集上的分类准确率曲线。当样本维数小于40时，五种分类算法的分类准确率曲线大致保持一致；样本维数大于40时，RF算法和ELM算法的分类准确率呈下降趋势；当维数为60时，OS-ELM算法的分类性能达到97%，但随着维数的升高，其分类性能不断降低。相比较之下，MLELM和DSAE算法受维数增加的影响较小，而当维数大于100后，DSAE的分类性能保持稳定，明显优于对比算法。

图4(b)为五种分类算法在IMM数据集上的分类准确率曲线。当样本维数小于50时，ELM相关算法的分类性能优于随机森林算法，当维数大于50时，RF的分类曲线在OS-ELM算法之上; 随着维数的升高ELM的准确率不断下降，当样本维数大于80时，DSAE的分类准确率优于其他四种算法。

图4(c)为五种分类算法在Yale数据集上的分类准确率曲线。当维数小于50时，OS-ELM算法的分类准确率高于其他算法；但当维数大于50后，分类性能明显下降并且表现不稳定，RF算法在此数据集上的分类效果较差。相比之下，MLELM与DSAE的分类性能明显优于其他算法。

图4(d)为五种分类算法在UMIST数据集上的分类准确率曲线。当样本维数大于10时，五种算法的分类性能都较好，OS-ELM与RF的分类性能相差不大，相比之下，ELM、MLELM和DSAE的分类准确率更高。

图4 不同样本维数的分类准确率变化

由图4可看出，随着输入人脸图像特征的增多，ELM、RF、OS-ELM和MLELM算法的分类准确率会不断降低，因此OS-ELM与RF算法不适合对高维数据进行分类，多层结构MLELM虽受维度的影响较小，但分类准确率也明显下降; 而DSAE算法的分类准确率虽然也有所降低，但整体上的分类效果受样本维数的影响较小。因此DSAE算法能够充分利用样本的低秩信息，对于噪声数据的抗干扰能力更强。

图5给出了ELM、OS-ELM、MLELM和DSAE在ORL、IMM、Yale和UMIST数据集上随着隐层节点数的改变，四种算法的分类准确率的变化情况。其中X轴表示隐层节点数，Y轴表示30次实验的平均分类准确率。

图5 不同隐层节点数的分类准确率变化

在图5(a)中，对于ORL数据集，当样本维数(dim)为140时，第一个隐层节点数大于300时，DSAE的分类准确率大于ELM、OS-ELM和MLELM算法。在图5(b)中，对于IMM数据集，当样本维数为130时，OS-ELM与ELM的分类效果较差，隐层节点数小于400时，MLELM与DSAE的分类效果大致相同，当节点数大于400时，DSAE的分类性能更好。在图5(c)中，对于Yale数据集，当样本维数为140时，ELM、MLELM和DASE的分类性能较好。在图5(d)中，对于UMIST数据集，当样本维数为40时，五种分类算法的分类性能都较好，当隐层节点数小于600时，MLELM算法的分类准确率高于DSAE和ELM。当节点数大于600时，ELM、MLELM与和DSAE的分类效果大致相同，其中，隐层节点数为1 000时，DSAE的分类效果最好。

表2给出了ELM、RF、OS-ELM、MLELM、DSAE分别在四种数据集下30次实验的平均分类准确率和标准偏差，当ORL、IMM和Yale数据集在维数分别为135、120、100、65的情况下，与MLELM相比，DSAE的分类准确率约提高3%，DSAE的整体分类性能好且偏差较小。

另外，图6还展示了ORL人脸数据集中三张人脸图像样本的分类结果，DSAE模型皆将其分类正确，而ELM和MLELM都将其分类错误。

表2 五种分类算法的分类准确率对比

图6 三个人脸图像的分类结果

与MLELM相比，DSAE对误差模型采用截断式核范数正则化进行约束，并采用极端学习机自编码器的深层结构将输入的原始图像数据一层一层地抽象，得到更能描述图像本质的稀疏特征，更好地提取输入原始图像中最重要的信息用于训练模型，从而提高模型的分类性能。

4 结语

本文借助极端学习机和自编码器提出一种用于人脸图像的深度稀疏自编码器方法。通过加入截断式核范数正则化项对损失函数进行优化，提取人脸图像的主要信息和特征，摒弃噪声数据，将原始人脸图像映射到一个新的稀疏特征表示空间。实验结果表明，本文方法对于高维人脸图像的识别率有明显提高。