基于拉普拉斯评分的多标记特征选择算法

胡敏杰，林耀进,王晨曦，唐 莉，郑荔平

(闽南师范大学 计算机学院，福建 漳州 363000)(*通信作者电子邮箱zzhuminjie@sina.com)

0 引言

多标记学习是目前机器学习、模式识别和数据挖掘等领域的研究热点之一[1-5]。多标记学习中每个样本不仅由一组特征向量描述,还可能同时有多个语义，将多个语义设计成多个标记。例如：在图像标注[1]中，一幅图同时具有“沙漠”“蓝天”“风景”等几个语义信息；在文本分类学习[3]中，一篇文档具有“上海世博会”“经济”和“志愿者”等几个主题；在音乐乐曲[4]中，一首乐曲可能同时具有 “放松”“幸福”“安静”和“难过”等几个情感语义。多标记学习中多个语义标记并不互斥，因此有别于单标记学习中的多个类别。多标记学习不仅需要了解利用多个标记之间的信息，同时仍然需要解决冗余特征、维数灾难等问题。

一种常用的解决冗余特征和维数灾难问题的有效方案是降维技术。目前多标记特征降维方案中主要是特征转换和特征选择。将原始高维特征空间变换或映射到低维空间来表示样本，这一过程称之为特征转换，如基于最大依赖的多标记维数约简方法(Multi-label Dimensionality reduction via Dependence Maximization, MDDM)[5]；在原始高维特征空间中利用一定的评价准则选择一组能获得相同甚至更高分类性能的原始特征集子集，这一过程称之为特征选择。相比重建了特征新空间的特征转换方案，特征选择对后续学习分析数据保留了特征的物理意义。特征选择过程中常见的评价准则有信息度量[6-7]、依赖性度量[8]和谱图理论[9-12]等。

基于拉普拉斯评分(Laplacian score)的特征选择算法[9]是谱图理论的特征选择模型的典型算法之一。拉普拉斯特征评价算法对单个特征进行评判得分，选出有较高方差和较强局部几何结构保持能力的特征。该算法简单易理解，但该算法不但没有考虑特征之间的关联性且仅针对单一标记评价特征，而多标记学习面临多个标记的评分。Alalga等[11]利用半监督对没有标记的数据远远大于有标记的数据集进行软约束的拉普拉斯特征选择，利用部分样本的标记信息构建有标记数据集中样本间的关联系数来约束核函数构建权重矩阵，该算法主要实现了在标记不易获取仅部分样本被标记的数据集中拉普拉斯特征选择算法的实现；Yan等[12]利用样本多个标记的Jaccard相似性来构建样本的相似性矩阵，从而提出基于图谱的多标记特征选择算法，该算法不仅有效利用了类标间的关联信息，且算法不依赖具体的多标记分类算法或问题转化。以上两种算法均仅考虑样本的多个标记间共同关联的相关性，且未考虑特征之间的相关性, 因此，本文在拉普拉斯评分的评价准则上不仅考虑特征之间的关联性，同时考察样本在多个标记间共同关联和共同不关联的相关性，重新构建基于多标记的拉普拉斯评分中的样本相似性矩阵，从而提出了一种基于拉普拉斯评分的多标记特征算法。

1 传统拉普拉斯特征选择算法

拉普拉斯评分基于拉普拉斯特征映射和局部保持投影理论。假设Fr表示数据集中第r个特征，fir和fi′r分别表示第r个特征上的第i、i′(1≤i,i′≤m)个样本的取值，xi、xi′分别表示第i、i′(1≤i,i′≤m)个样本点,yi、yi′分别表示第i、i′(1≤i,i′≤m)个样本的标记类别。算法思路如下：

第一步 构建近邻无向有权图G(V,E)。各样本作为节点表示图节点集V，样本间的近邻关系表示图中的边形成边集E。如果样本xi是样本xi′的最近邻的k个样本之一或xi′是xi最近邻的k个样本之一，则xi与xi′节点相连成边。

第二步 生成样本间的相似矩阵S。根据数据是否携带标记信息，拉普拉斯特征选择算法在构建样本权重矩阵时分为两种。

1)不考虑标记信息，通过核函数构造权重矩阵，如式(1):

(1)

2)对具有单一标记的数据，常根据类别个数来构建相似矩阵，如式(2):

(2)

其中：t是参数，一般取1；nk为类别为k的样本个数。

第三步 生成拉普拉斯矩阵L。在无向有权图G中，令邻接矩阵Wii′=Sii′(1≤i,i′≤m),且W为对称矩阵，则度矩阵D为:

(3)

度矩阵诠释了每个样本周围聚集其他样本的密集程度，值越大说明与之样本靠近的其他样本就越多。由度矩阵和邻接矩阵得到相应的Laplacian矩阵L和正则化的Laplacian矩阵L：

(4)

第四步 拉普拉斯评分特征选择。根据谱图理论，Laplacian矩阵的特征值和特征向量能体现样本分布的结构。因此拉普拉斯评分算法选取那些特征向量值的分布与样本分布保持一致的可分性强的特征，即选择那些使得式(5)取较小值的特征[9]:

(5)

其中：ur表示第r个特征fr的期望值，定义[9]如式(6):

(6)

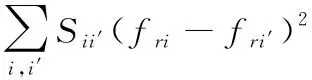
2 多标记的拉普拉斯特征选择算法

2.1 样本相似度的构建

由于传统拉普拉斯特征选择算法适应单一标记的学习，而在多标记学习中每个样本可能与多个语义标记关联，因而无法按单一标记中通过类别个数来构建样本的相似度。单标记学习中标记里的信息表示的是样本属于哪一类，而多标记学习中标记的信息表达的是与该标记是否相关。如表1中列举有5个样本x1、x2、x3、x4、x5和3个标记信息y1、y2、y3。

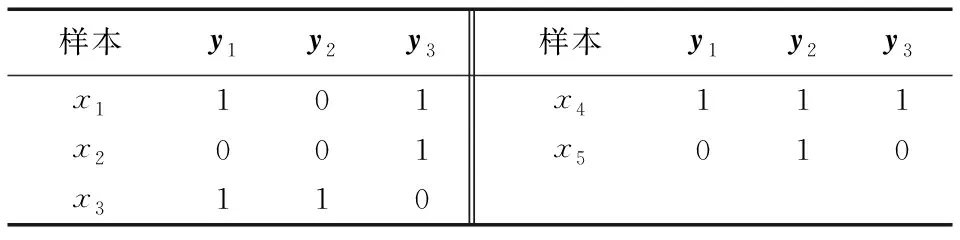
表1 一个多标记数据集例子

在表1中，1表示样本与这个标记信息关联，而0表示不关联。如y1标记中样本x1、x3、x4标记为1，表示样本x1、x3、x4与标记y1相关联，而样本x2、x5标记为0表示与标记y1不关联。若将标记信息里的0和1看成两个类别，那么可以理解成在标记y1下样本x1、x3、x4为同一类，而样本x2、x5为另一类，因此可以依照传统拉普拉斯评分算法中式(2)构建y1标记下的样本相似矩阵，如表2所示。

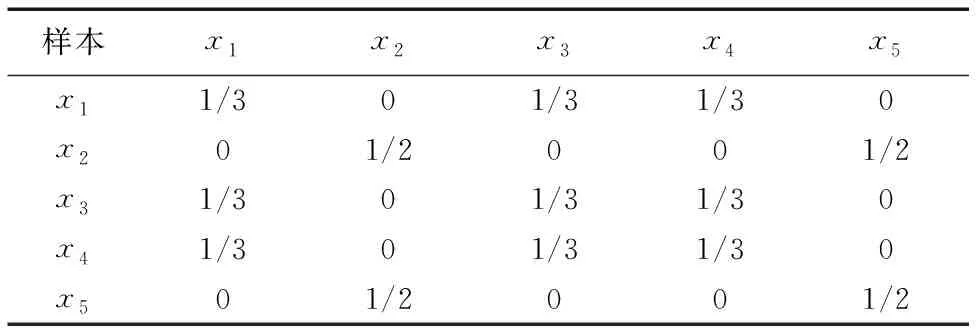
表2 标记y1下样本的相似度

以此类推，可以建立各标记下的样本相似矩阵，如果各标记间相互独立那么采用传统拉普拉斯评分算法可求得各标记下的特征序列，然后对各标记下的特征序列融合以期求得最终的特征序列，但该方法并未探索样本在整体标记空间中的相似程度。严鹏等[10]利用Jaccard相关性来衡量两个样本间在整体标记空间的相似程度，即对两个样本的标记集中用关联标记的交集元素个数除以关联标记的并集元素个数。如样本x1与标记y1、y3关联，样本x2与标记y3关联，因此样本x1、x2关联的标记交集为y3，关联标记的并集为y1、y3，所以样本x1和样本x2相似度为1/2。依此严鹏等建立样本在整体标记空间的相似矩阵如表3所示。

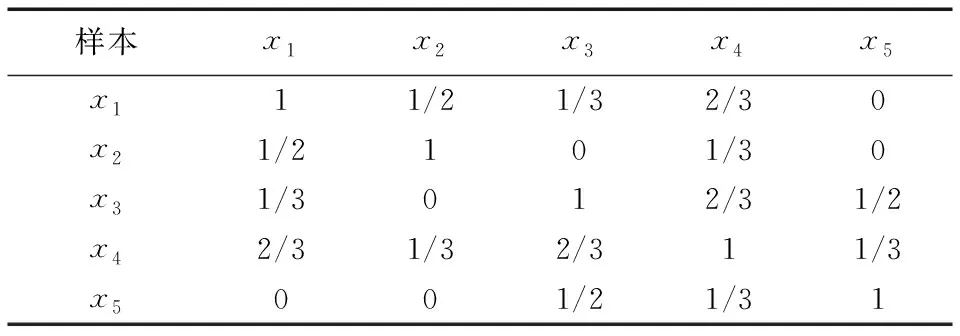
表3 Jaccard相关性下的样本的相似度

受单标记类标记含义启发，样本x2和样本x5在单标记y1下属于0类，在多标记含义下样本x2和样本x5都不与y1标记关联。

但严鹏等只对两样本关联的标记寻求关系，而现实中两样本不与某些标记关联也隐藏着一定的关系。如样本x1和x2都不与标记y2关联，都与标记y3关联，将共同关联和共同不关联的都认可为样本之间的相似度, 因此可设计一种新的多标记下拉普拉斯评分算法的样本相似度S=(|Y|-|Y1⊕Y2|)/|Y|,其中Y1和Y2分别表示两样本的标记集。依此设计表1中样本在整体标记空间的相似矩阵如表4所示。

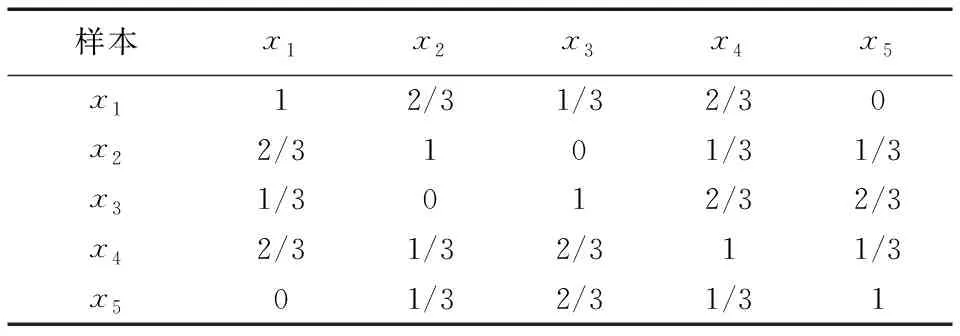
表4 共同关联和共同不关联下的样本的相似度

表2中样本x2和x5在单标记y1下具有相似度为1/2,而表3中只考虑与标记共同关联性，样本x2和x5完全不相似，即相似度为0，但表4中同时考虑与标记共同关联和共同不关联性，样本x2和x5具有1/3的相似度，由此表4更能保留说明样本在整体标记空间的相似情况。

2.2 基于拉普拉斯评分的多标记特征选择算法

由于传统的拉普拉斯特征选择算法只度量单个特征的可分性，而未考虑特征之间的冗余性和相关性，因此在计算了样本在多个标记空间的相似度后，在评价特征的可分性上考虑特征之间的相关性。设多标记训练集T={(xi,yi)|1≤i≤m}，其中，X={x1,x2,…,xm}表示样本空间，样本的标记集为Y={y1,y2,…,yi,…,ym}且yi={l1,l2,…,lq}表示由q个标记组成的标记向量(1≤i≤m)，若样本xi(1≤i≤m)与lj(1≤j≤q)标记相关，则yij=1,否则yij=0。F={f1,f2,…,fn}表示描述样本的特征向量，fir表示第r(1≤r≤n)特征上第i(1≤i≤m)个样本的取值。

定义1 给定描述样本的数据集和样本的标记集Y={y1,…,yi,…,ym}，则样本在整体标记空间的相似性矩阵S′和度矩阵D′分别为：

(7)

由此相应的Laplacian矩阵L′和正则化的Laplacian矩阵L′为：

定义2 给定描述样本的数据集T和特征集F，当已知S′、D′、L′时，在整体标记空间下特征之间的相关性的目标函数为：

(8)

其中Fs′表示已选特征的子集。式(8)中分母通过各特征的均方差度量特征的区分能力，均方差越大，该特征集区分能力越强；式(8)的分子用欧氏距离计算各特征间的关联性，分子越小特征子集对样本分布结构保持能力越强, 使得式(8)获较小值的特征子集能实现对样本标记的识别力。因此式(8)的定义考虑了整体标记空间下特征间的相关性。

定义3 给定描述样本的数据集和特征集，当已知S′、D′、φ(Fs′)时，候选特征中能加强现有特征子集Fs′对标记识别能力的特征定义为：

(9)

其中，Fu表示候选特征的集合，评估一个候选特征是否加入已选特征集中取决于该特征能否使得同类样本取值接近而不同类样本取值差异大。而对多个可加强已选特征集的候选特征，由式(9)可知，新加入的候选特征使φ(Fs′)越小越好，因此在多个具有提升已选特征子集能力的候选特征中选择使φ(Fs′∪fi)-φ(Fs′)最小的一个特征, 因此式(9)的定义可以找到一组具有更强识别力的特征集。

2.3 算法步骤

本文提出了一种基于拉普拉斯评分的多标记特征选择算法。该算法首先针对多标记学习中每个样本可能具有的多个语义标记信息重新计算了样本之间的相似度，从而构建了样本在整体标记空间的相似矩阵；然后在建立的样本相似矩阵上利用传统的拉普拉斯评分算法找出特征集中最强识别力的一个特征；接着以该特征作为已选特征，根据定义2中式(8)和定义3中式(9)依次评价候选特征与已选特征的相关性与冗余性，选出识别力强于未组合时的最强一个特征，并加入已选特征集；最后对余下候选特征进行下一轮迭代，以期生成特征重要度排序集。

根据上述分析，一种基于拉普拉斯评分的多标记特征选择算法(multi-label feature selection algorithm based on Laplacian score，MLLAP)的具体描述如算法1所示。

算法1 MLLAP算法。

输入 多标记数据集T；

输出 特征序列Fs。

步骤1 初始化已选特征集Fs=∅，候选特征集Fu={f1,f2,…,fn}。

步骤2 依据定义1中式(7)计算两个样本间的相似度矩阵S′和度矩阵D′。

步骤3 根据式(5)求出最具有识别力的一个特征fi，更新Fs=Fs∪fi,Fu=Fu-{fi};

步骤4 根据式(8)和(9)依次判断Fu中候选特征的得分L(i)=φ(Fs∪fi)-φ(Fs)，取每一轮最小值加入已选特征Fs。

步骤5 重复步骤4，直到Fu为空结束。

在算法1中，假设数据集中包含m个样本和n个特征。MLLAP算法的时间代价主要在：步骤2中计算两个样本间的相似度矩阵，时间复杂度为O(m2);步骤4～步骤5依次评价候选特征的时间复杂度为O(nlogn); 该算法不依赖任何分类器。

3 实验设计与结果分析

3.1 实验数据

为了检验算法的有效性，本文在mulan数据库(http://mulan.sourceforge.net/datasets.html)中选取6个多标记数据集进行验证，各数据集描述信息见表5。

3.2 实验设置

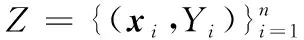
HL用来度量样本在单一标记上的错误分类情况，定义为：

其中Zi表示预测到的标记集。

OE用来衡量在样本的相关标记排序里排在第1位的标记不属于样本相关标记的样本所占的比例：

其中:若l∉Yi,则w(l)=1; 否则w(l)=0。

CV用来度量样本在测试集上搜索与该样本相关的标记所需的平均次数，定义为：

RL用来度量错误标记排在正确标记之前的比例，定义为：

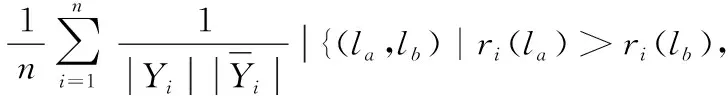
AP用来统计在样本的标记排序组里，排在该样本正确标记前的标记仍为正确标记的平均比例，定义为：

以上5种评价指标中，AP指标取值越大学习性能越优，最优值为1；HL、OE、CV和RL指标取值越小越好，最优值是0。

本文选择其他4个对比算法分别为：使用线性核和非线性核的基于最大依赖的多标记维数约简方法MDDMspc[15]和MDDMproj[15]，基于贝叶斯分类器的多标记特征选择算法(Feature selection for multi-label naive Bayes classification, MLNB)[16]和基于多元互信息的多标记分类特征选择算法(Feature selection for multi-label classification using multivariate mutual information, PMU)[17]。采用多标记学习算法(Multi-label Learning based onkNN, ML-kNN)[18]来评估特征选择后的性能，实验中ML-kNN的近邻k=10,平滑参数s=1。

3.3 实验结果与分析

为了验证所提算法的有效性，实验中首先将所提MLLAP算法与MLNB、PMU、MDDMspc及MDDMproj算法诱导出来的特征子集的分类性能进行对比，并且分析各算法的分类性能随特征数目增加而变化的情况；然后检验MLLAP算法与其他4个算法是否存在显著性差异。由于所提MLLAP算法和PMU、MDDMspc及MDDMproj得到的是一组特征排序，因此实验中选取特征排序的前k个特征作为特征子集，其中k为MLNB算法所得特征数。表6～10列出了5种对比算法在6个数据集5个评价指标下的实验结果。

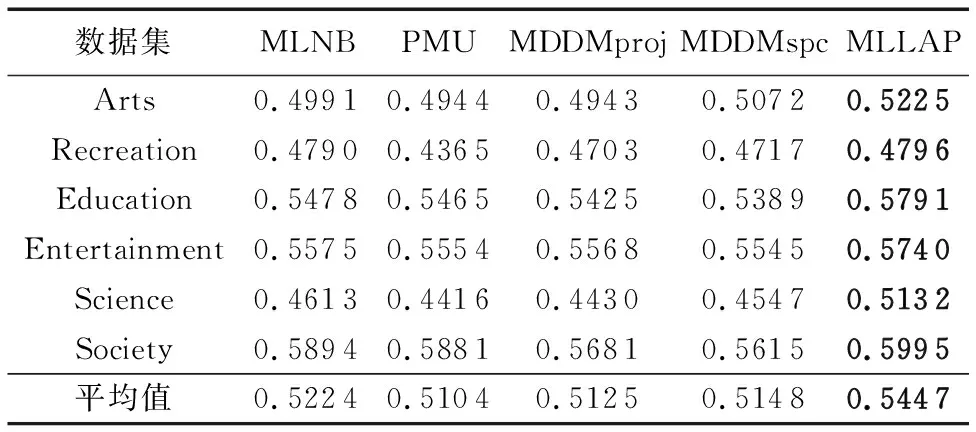
表6 各算法在AP评价指标下的分类性能比较

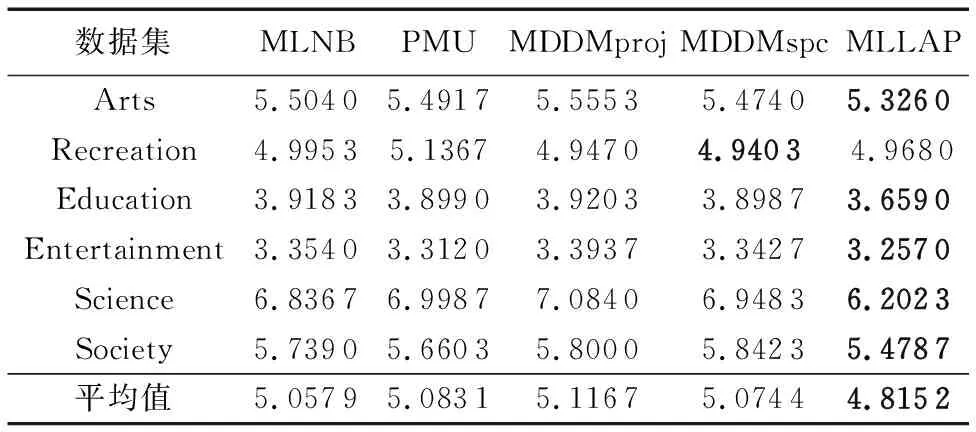
表7 各算法在CV评价指标下的分类性能比较

表8 各算法在HL评价指标下的分类性能比较

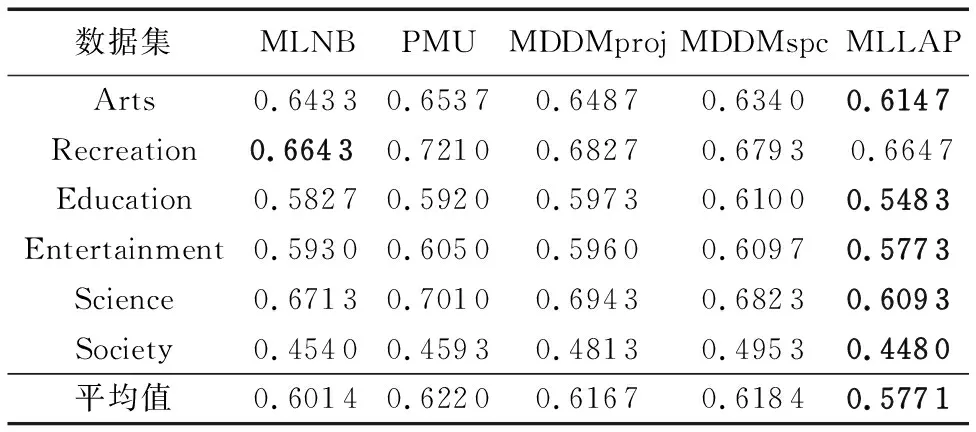
表9 各算法在OE评价指标下的分类性能比较

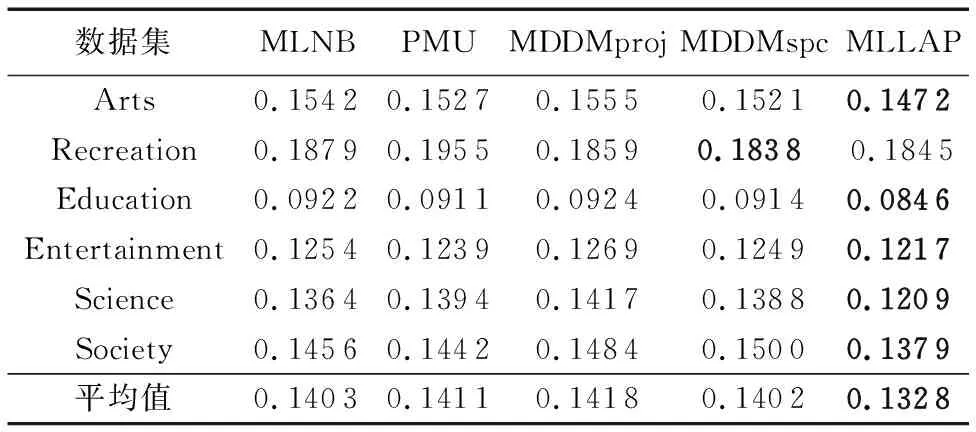
表10 各算法在RL评价指标下的分类性能比较

由表6～10发现：

1)MLLAP算法在6个数据集、5个评价指标共30个实验结果上仅4个实验数据略差，优胜率达86.66%。其中MLLAP算法完胜PMU、MDDMproj算法，与MLNB、MDDMspc算法相比，在2个数据集上各有2个指标稍差。

2)从平均分类精度来看，MLLAP算法在5个评价指标下均获得最优，其中AP、CV、HL、OE指标中相比次优的MLNB算法分别高出4.3%、4.7%、1.5%、4.1%，RL指标中相比次优算法MDDMspc胜出5.3%。

上述实验分析表明MLLAP算法生成的特征重要度排序中前k个特征诱导的分类性能平均上优于MLNB、PMU、MDDMproj及MDDMspc算法。为了更精确地了解MLLAP算法选取重要特征的能力，图1～5从整体上对比各算法的分类性能随选取特征数目的变化而变化的情况。

从图1～5可以发现：

1)从图1中AP指标、图2中CV指标，图5中RL指标来看，MLLAP算法的分类精度曲线走势清晰地、显著性地优于MLNB、MDDMproj及MDDMspc算法，与PMU算法相比，仅在Education数据集上对初始特征的选取略差，但特征选取达100左右时MLLAP算法的优势立即体现出来。说明随着特征的选取加入，MLLAP算法获得的重要特征能力比其他4个算法强，能以合理或相同数量的特征就达到较好的分类性能。

2)从图3中HL指标和图4中OE指标来看，在Recreation、Science和Society数据集上MLLAP算法的分类精度曲线走势整体上依然优于MLNB、MDDMproj、MDDMspc及PMU算法。对Arts和Education数据集来看，MLLAP算法的走势图与PMU算法在特征选取的初步不期伯仲，但在特征数量达到一定程度时，MLLAP算法的性能即体现出来。对Entertainment数据集来看，在OE指标下当特征数在200以内时,MLLAP算法明显优胜于其他4个对比算法，但随着特征数的增加，MLLAP算法与其他算法走势曲线交融，因而也解释了表4中MLLAP算法没有最优的原因。

图1 在评价指标平均查准率下各算法对数据集的分类性能趋势

3)以图1～5的Recreation数据集来看，MLLAP算法的走势图在各评价指标下以极少的特征数量就达到相当好的分类性能，但随着选取特征的增加，分类性能相比自身出现回落，以MLNB算法选取的特征数为目标时，MLNB算法和MDDMspc算法的走势图出现重叠，从而不分伯仲，由此也解释了表3～6中MLLAP算法在Recreation数据集上没有最优的原因。

4)从图1～5整体来看，MLLAP算法所选取的特征重要度排序是有效的，该算法能以较少的合理的特征数就达到很好的稳定的分类性能。

图2 在评价指标覆盖范围下各算法对数据集的分类性能趋势

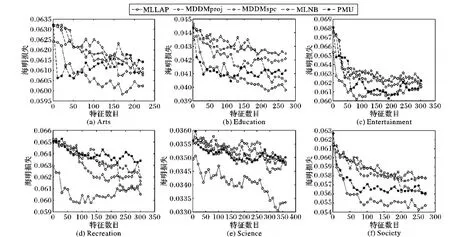
图3 在评价指标海明损失下各算法对数据集的分类性能趋势

通过对比各个算法的k个特征诱导出来的分类精度及分类精度随特征数增加而变化的情况，说明了MLLAP算法的有效性。为了更进一步突出MLLAP算法相比其他4个算法的优势，本文先假设5个对比算法在5个评价指标下都性能相等，采用显著性水平0.1的Friedman test[19]进行检验，经检验都拒绝了该假设，即5个对比算法在5个评价指标下是存在性能差异的。因此，进一步采用显著性水平为0.1的Bonferroni-Dunn test[20]来分析具体差异情况，观察本文MLLAP算法与其他MLNB、PMU、MDDMproj及MDDMspc算法在6个数据集上的平均排序是否高于临界差(Critical Difference, CD)，若高于则认为MLLAP算法与其他算法之间有差异。

表11给出了5个算法在5个评价指标下的平均排序值。

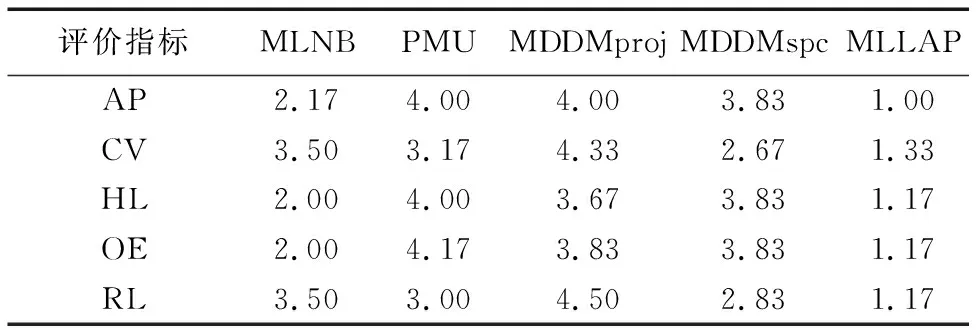
表11 5个对比算法在5个评价指标下的平均排序

图4 在评价指标单错误下各算法对数据集的分类性能趋势

图5 在评价指标排位损失下各算法对数据集的分类性能趋势

从图6发现：MLLAP算法在AP、HL和OE指标下与算法MLNB相当，比PMU、MDDMspc和MDDMproj算法存在显著性优异；在CV和RL评价指标下，与算法PMU和MDDMspc性能相当，比MLNB和MDDMproj算法性能显著提高；在5个评价指标下，MLLAP算法都优于MDDMproj算法。

总体来说，MLLAP算法性能最好，在5个评价指标下不仅平均分类性能最优，而且与其他4个对比算法存在显著性优异达65%。

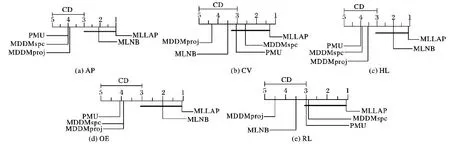
图6 在5个评价指标下各算法的性能差异

4 结语

传统拉普拉斯评分特征选择算法只适应单标记学习任务，本文在多标记学习中考虑样本之间与多个标记共同关联和共同不关联的关系构建样本在整体标记空间的相似度矩阵，从而实现拉普拉斯评分算法在多标记数据集上的特征选择，同时在传统拉普拉斯评分的基础上考虑了特征间的相关性及冗余性。本文算法直接关注传统拉普拉斯评分算法在多标记学习中如何构建有效的样本相似度矩阵，并未考虑多标记数据集中标记间的相关性，也未进一步探索所选特征具体由哪些类别标记决定，未来将致力于研究类属属性。