基于增强特征判别性的典型相关分析和分类集成的助学金预测方法

张芳娟，杨 燕，杜圣东

(1.西南交通大学 信息科学与技术学院，成都 611756； 2.四川省云计算与智能技术高校重点实验室(西南交通大学)，成都 611756)(*通信作者电子邮箱yyang@swjtu.edu.cn)

0 引言

随着信息技术的发展，特别是教育信息化的发展，数据驱动下的教育改革逐渐成为研究热点。助学金评定工作作为高等院校一项重要的工作，传统的评定方法大多是通过大量的学生个人问卷调查及其他相关信息来完成，评定过程工作量大且管理效率低。在高校管理逐渐数字化的背景下，使得高校学生助学金的便捷、高效预测成为可能。国内外有关助学金评定方法的研究和相关工作很少，因此，对于助学金评定方法的研究具有很大实际意义。

学生的经济情况跟学生的在校行为(一卡通的消费金额、消费方式、学习习惯等)是紧密相关的。利用学生的生活行为数据和学习表现数据能够更加真实和准确地预测需要资助的学生。学生在校行为数据是多源异构数据，如果将数据集进行简单的组合，不能充分利用数据间的关联、互补信息，而多视图学习能在学习过程中考虑到不同视图信息间的相互联系[1-2]，因此，将学生在校行为数据从学习维度和生活维度划分为两个不同视图，增强判别典型相关方法利用视图间的关联、互补信息，获得优于仅仅基于单视图数据学习的性能[3]。

典型相关分析(Canonical Correlation Analysis, CCA)[4]通过最大化视图间的相关性获得较单一视图更好的学习效果, 但是作为无监督特征处理方法，基于CCA建立分类模型未必会获得好效果。Sun等[3]在CCA的基础上提出了判别典型相关分析(Discriminative Canonical Correlation Analysis, DCCA)，DCCA的优化目标在于使得类内相关性最大的同时类间相关性最小，但是没有针对分类预测任务优化组合特征本身; 周旭东等[5]也在CCA的基础上提出了增强视图组合特征判别性的典型相关分析(Combined-feature-discriminability Enhanced Canonical Correlation Analysis，CECCA)，其优化目标考虑了视图组合特征的判别性，但是忽略了类别之间的相关性; Xing等[6]在CCA的基础上提出了完善的典型相关分析(Complete Canonical Correlation Analysis, C3A)，C3A在计算耗时、耗资源方面得到了优化，该优化目标并不是专门针对分类预测任务。上述方法虽然都各有优点，但并不是专门针对分类预测任务，没有综合考虑视图组合特征的判别性和视图类别相关性, 因此，本文提出一种增强判别性的典型相关算法。一方面将视图的类间和类内相关性考虑进来，在最大化类内相关的同时最小化类间相关； 另一方面考虑了视图组合特征的判别性，从而达到增强特征判别性的目的，提高分类预测性能。

分类集成通过组合多个个体分类器来构建一个高精度的分类器，从而改善单个分类器的不稳定性同时提升分类预测准确率[7]。文献[8-10]基于单一分类器构建集成模型，主要针对文本分类问题；文献[11]采用加权投票法将支持向量机(Support Vector Machine, SVM)、朴素贝叶斯(Naive Bayes, NB)和逻辑回归三种不同方法进行集成，获得优于单个分类器的结果。相比上述几种集成方法, 分类熵集成(Classification Entry, CE)[12]方法不仅考虑分类器的整体性能，而且还考虑了个体分类器的局部性能，可以自适应地为各个分类器分配权值，因此，高校助学金的预测模型基于EN-DCCA和分类熵集成策略构建。K最近邻(K-Nearest Neighbor,KNN)方法简单, 适用于大部分样本集；随机森林(Random Forest, RF)本身作为一种集成方法，能获得较好的分类预测性能；朴素贝叶斯在小样本集上也能获得较好的效果，所以利用KNN、RF和NB三种方法作为个体分类器[13-14]。

1 相关原理

1.1 判别典型相关分析

设有来自c个类别的n对数据样本集{(xi,yi)}∈Rp×Rq，其中，xi和yi分别来自两个不同的视图。记样本集X=[x1,x2,…,xn]∈Rp×n,表示X有n个样本，每个样本有p个特征属性; 记样本集Y=[y1,y2,…,yn]∈Rq×n，Y也有n个样本，每个样本有q个特征属性。

DCCA的优化函数是最大化类内相关且同时最小化类间相关，在该目标下获得样本集X和样本集Y的投影向量wx和wy，DCCA的优化目标定义为：

s.t.wxTCxxwx=1,wyTCyywy=1

(1)

其中:Cw为类内相关矩阵，E[·]是数学期望，Cxx、Cyy分别为样本集X、Y的自协方差矩阵，且Cxx=E[XXT]=XXT、Cyy=E[YYT]=YYT。

通过使用Lagrange乘子法，该问题的求解可通过解式(2)广义特征值问题得到：

(2)

1.2 增强组合特征判别分析

跟DCCA定义方式相同，且记X=[x1,x2,…,xn]∈Rp×n，Y=[y1,y2,…,yn]∈Rq×n。设样本集X、Y来自c个不同的类别，CECCA算法的优化目标是在CCA的优化目标函数中加入线性判别分析项，由于样本X、Y的组合特征有并行化组合和串行组合两种组合方式,因此，CECCA对应有CECCA_P和CECCA_S两种具体算法，分别对并行组合特征和串行组合特征进行优化，从而得到视图X、Y的投影向量wx和wy。

下面以CECCA_P进行说明，并行化组合特征的CECCA优化目标为：

s.t.wxTCxxwx=1,wyTCyywy=1

(3)

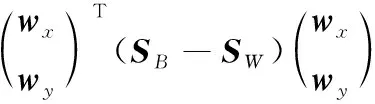
利用Lagrange乘子法，该优化问题可通过求解式(4)广义特征值得到：

(4)

1.3 信息融合方法

Sun等[15]首次使用CCA方法实现了信息的特征融合。特征投影向量wx和wy将数据集X、Y分别映射为典型相关属性特征wxTX、wyTY，wxTX和wyTY有串行组合和并行组合两种方式。

串行融合：

(5)

并行融合：

(6)

基于分类建立模型时，利用上述信息融合方法便可得到融合之后的组合属性特征，再将该组合特征用于分类预测任务。

1.4 分类熵集成

分类熵集成[12]同时考虑分类器的整体性能和个体分类器的局部性能，并且可以自适应分配权值。文献[12]对该算法进行了详细描述，设L为类别个数，算法主要包括以下4个步骤：

1)计算个体分类器的混淆矩阵；

2)计算全局准确率和局部准确率；

3)根据全局准确率和局部准确率计算个体分类器输出类别的权重，在此基础上计算分类熵CEj，j表示类别；

4)集成分类器输出类别。

(7)

2 增强特征判别性的典型相关分析算法

增强特征判别性的典型相关分析(Enhanced-Discriminative Canonical Correlations Analysis, EN-DCCA)算法在判别典型相关分析(DCCA)方法的基础上引入判别分析项，同时考虑了视图类别的相关性和视图组合特征的判别性，可求得更具有判别性的典型相关特征，从而提高分类预测性能。

同样设有来自c个类别的n对数据样本集{(xi,yi)}∈Rp×Rq，其中，xi和yi分别来自两个不同的视图。记样本集X=[x1,x2,…,xn]∈Rp×n,表示X有n个样本，每个样本有p个特征属性，记样本集Y=[y1,y2,…,yn]∈Rq×n，Y也有n个样本，每个样本有q个特征属性。

EN-DCCA的优化目标最大化类内相关的同时最小化类间相关，而且考虑了组合特征的判别性，在这两者目标下获得两个视图的投影向量wx和wy；EN-DCCA属性特征并行组合的优化目标定义为：

s.t.wxTCxxwx=1,wyTCyywy=1

(8)

则EN-DCCA的优化目标可进一步简化为:

s.t.wxTCxxwx=1,wyTCyywy=1

(9)

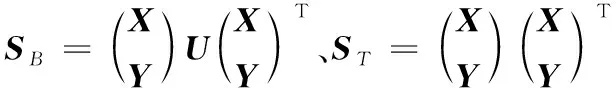
2wxTXAYTwy

s.t.wxTCxxwx=1,wyTCyywy=1

(10)

其中:A=2U-I，I为单位矩阵。

利用Lagrange乘子法，对优化目标建立Lagrange函数:

L(λ,wx,wy)=wxTCwwy+wxTXAXTwx+wyTYAYTwy+

2wxTXAYTwy-λ(wxTCxxwx+wyTCyywy-2)

(11)

对wx求偏导：

2XAYTwy-λ(XXTwx+wxTXXT)

(12)

化简则有:

(13)

同理可得：

(14)

(15)

(16)

因此EN-DCCA的优化模型可通过求解式(17)广义特征值问题得到。

(17)

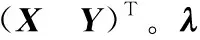
3 基于EN-DCCA和分类集成的预测模型

本文基于提出的增强视图特征判别性的典型相关分析算法EN-DCCA和分类集成方法来构建高校学生助学金预测模型。针对分类任务，EN-DCCA方法可以获得更具判别性的特征，利用分类集成方法进行预测，进一步提升预测准确率。

基于EN-DCCA和分类集成的高校助学金预测模型如图1所示。

图1 高校助学金预测模型

图1 所示的预测模型实施步骤如下：

1)数据预处理并获得判别典型相关特征。

学生在校行为数据一般都是多源异构数据，首先将数据预处理，得到生活行为和学习表现两个视图数据，然后利用EN-DCCA算法进行特征学习，获得增强判别性的典型相关特征。

2)构建分类集成模型实现资助金预测。

利用k-折交叉采样方法[17]对EN-DCCA方法学习的特征进行抽样，得到k个数据子集用于训练个体分类器，最后用分类熵集成策略实现助学金预测，并输出预测结果。

基于EN-DCCA和分类集成的助学金预测具体算法如下。

1) 基于EN-DCCA方法提取判别典型相关特征。

输入：视图X、Y，样本类别个数c；

输出：视图X、Y的投影矩阵wx、wy。

a)构建增强视图特征判别性优化目标；

b)计算Cw、Cxx、Cyy、A；

c)代入b)步计算的参数求解wx、wy；

d)计算判别典型相关特征wxTX、wyTY；

e)wxTX和wyTY信息融合；

2) 用分类集成方法完成预测。

输出：预测结果。

b)基于数据子集训练个体分类器；

c)利用分类熵集成方法对分类结果集成，最后输出预测结果。

4 实验及结果分析

4.1 数据集介绍及实验设计

本实验利用的数据来自多个学院8 376名本科生在校行为记录，主要包括6部分：一卡通消费记录、图书借阅记录、寝室门禁数据、图书馆门禁数据、学生成绩数据、助学金信息数据。其中学生的消费信息、图书借阅信息、寝室门禁、图书馆门禁数据来自学生的校园一卡通，每个数据集包含几百万条记录，按学生的ID号进行处理。通过一卡通的消费记录，可以提取出学生平均每周去食堂的消费次数、每次消费的金额、学校超市购物金额、打印资料费用等其他生活消费支出；寝室和图书馆门禁数据可以得到学生去图书馆自习的频次、自习时间长短以及学生早出晚归的时间等信息；图书借阅记录可以大致了解学生借阅的数量等信息。学生的助学金获得情况作为类别标签，分为4个类别：没有助学金、三等助学金、二等助学金和一等助学金。另外，考虑到学生隐私问题，学号、成绩等信息都经过脱敏处理。

为了能够充分利用数据之间的相关、互补信息，将多维度学生在校行为数据从学习和生活方面划分为两个不同视图，利用本文提出的EN-DCCA方法选择出更具判别性的特征，并与CCA[4]、DCCA[3]、CECCA[5]方法进行对比；然后利用基于KNN、RF、Naive Bayes的分类集成方法进行预测，并与基于单分类器的预测结果对比。

4.2 EN-DCCA特征提取

为了验证EN-DCCA算法特征提取的有效性，使用样本分布图展示效果。样本分布图是对特征利用主成分分析(Principal Component Analysis, PCA)[20]方法提取最重要的2维或3维特征展示样本的分离性或者聚集现象，以此观察目标特征是否具有判别性。本文分别选择了CCA、DCCA、CECCA方法与本文提出的EN-DCCA算法进行对比, 结果如图2所示。

图2 不同特征学习方法的样本分布情况

图2(a)是将学生生活视图数据和学生行为视图数据并行组合的原始样本分布情况；通过图2(b)可以看出, CCA仅考虑了视图数据间的相关性，并不具有判别性；从图2(c)和图2(d)可以发现, DCCA和CECCA不仅考虑了视图数据间的相关性而且考虑了视图的判别性；图2(e)说明EN-DCCA算法效果较DCCA和CECCA，类内更紧凑，类间差距更大，因此具有更强的类别判别性。类别1样本个数最多，表示不能获得助学金学生，类别4样本个数最少，代表能够获得一等助学金的学生，类别2和类别3分别代表获得三等和二等助学金的学生。

4.3 基于EN-DCCA和分类集成的资助金预测性能

为了说明本文提出的EN-DCCA和分类集成助学金预测模型的有效性，将EN-DCCA提取的增强判别性特征用分类集成模型(记为RKN-CE)识别，并与RF、KNN、NB等不同单分类算法的预测效果进行对比；选择CCA、DCCA、CECCA与EN-DCCA算法作对比。同时，为了说明将学生在校行为数据划分为两个不同视图先进行特征学习再识别的优越性，与单个视图也作了对比，单视图数据集是将数据集X、Y并行组合，记为XY[5]，其中，数据集X是学生的在校行为数据，数据集Y是学生的学习表现数据。对比方式是将单视图数据集XY不作任何处理，直接进行分类预测，并与EN-DCCA在相同分类集成方法下进行对比。先用训练数据集训练本文提出的预测模型，然后用测试数据集验证该模型的有效性，为了能够直观展示预测结果，用预测准确率来评价该模型的有效性。

图3给出了在RKN-CE集成方法下，对数据集XY，用CCA、DCCA、CECCA与EN-DCCA方法的10次实验结果对比，可以看出EN-DCCA方法的效果比CCA、DCCA、CECCA方法要好；同时，基于EN-DCCA特征学习的预测效果比XY单视图直接预测效果更优。图4给出了用EN-DCCA方法获得判别典型相关特征，然后用分类集成RKN-CE方法预测，并与单个分类算法RF、KNN、Naive Bayes的10次实验预测结果对比，可以看出分类集成RKN-CE模型较其他单分类器能获得更好的结果。

图3 EN-DCCA与其他方法识别率对比

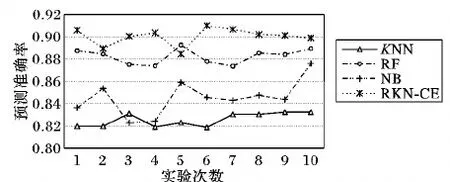
图4 RKN-CE与单分类算法识别率对比曲线

表1是单视图数据集XY、典型相关特征学习方法CCA、DCCA、CECCA、EN-DCCA处理的数据集分别用单分类器RF、KNN、NB和分类集成RKN-CE方法进行10次实验得到的平均结果。最后一行的平均值表示同一种特征学习方法在不同分类器下的一个平均结果，加粗的值表示同一种分类方法针对不同特征学习算法的最好预测结果。本文提出的EN-DCCA和RKN-CE模型的预测平均值为90.01%，较其他典型相关特征学习方法和分类方法组合效果都好，且EN-DCCA特征学习方法在不同分类方法下的预测平均值为86.33%，平均识别效果优于其他特征学习方法。

表1 助学金预测平均识别准确率 %

5 结语

本文提出一种多视图特征判别方法EN-DCCA，同时考虑了视图特征间的相关性和视图组合特征的判别性，并结合分类集成方法，构建了一种高校助学金预测模型。首先，将学生在校行为数据从生活和学习两方面处理为两个不同视图; 然后用EN-DCCA特征判别方法对两个视图数据进行特征学习，将得到的增强判别典型相关特征用分类集成方法进行预测识别。为了说明EN-DCCA方法的有效性，分别与已有的典型相关分析方法DCCA、CECCA等进行了对比，实验结果表明，基于EN-DCCA的特征学习方法识别率更好；同时，为了说明分类集成方法的优越性，与单分类算法进行了对比，最终实验结果表明基于EN-DCCA和分类集成模型能有效实现高校助学金预测。EN-DCCA方法主要针对两个视图进行特征学习，在后续的研究中希望将该方法扩展到三个及以上视图中。