基于模拟退火与贪心策略的平衡聚类算法

唐海波，林煜明，李 优，蔡国永

(1.广西可信软件重点实验室(桂林电子科技大学)，广西 桂林 541004; 2.广西自动检测技术与仪器重点实验室(桂林电子科技大学)，广西 桂林 541004)(*通信作者电子邮箱ymlin@guet.edu.cn)

0 引言

随着知识化、智能化时代的到来，人们已经认识到，对现实中产生的数据利用数据挖掘算法可以从中挖掘未知知识来获得巨大价值。聚类作为数据挖掘领域的一个常用算法，也是机器学习中广泛运用的无监督学习方法，它可以在无任何先验知识数据集中发现其潜在模式。自20世纪60年代至今，多种不同的聚类算法相继被提出，包括K-Means[1]、层次聚类[1]、DBSCAN(Density-Based Spatial Clustering of Applications with Noise)[1-2]、Fuzzy C-Means(FCM)[1,3]、谱聚类[1,4]等,并被广泛应用到多个领域，如模式识别、图像处理、信息检索等[1,5-7]。

平衡聚类的任务是保证聚类结果在传统聚类评价指标下有较好表现的同时，让每个簇的规模也尽可能相同, 因此，平衡聚类的聚类结果总具有一定的平衡性，这样可以避免聚类产生相对于多数簇而言过大或者过小的簇。然而传统的聚类算法，如K-Means、DBSCAN、FCM、谱聚类等在聚类的目标簇数目过大时，很难保证聚类结果也能够有较好的平衡性。

平衡聚类在数据挖掘中也有着重要的应用意义。许多实际应用场景对聚类结果的平衡性都提出了要求，例如在图像检索方面[8]，后台应用经过分析用户查询的语义，需要返回的内容可能涵盖多种类别，在没有进一步过滤信息情况下，后台算法返回的数据需要覆盖每个类并且尽可能平衡；在无线传感网中，不均衡的传感器分布结构可能造成网络中不均衡的能源消耗，进而影响网络的寿命[9]；在课堂教学分组中，使用聚类算法对班级学生进行聚类，结果中每个簇的规模所代表的小组人数应该尽可能相同。

平衡聚类作为聚类问题的一个子集也面临着效率的问题。由于许多聚类算法都是基于K-Means进行的改进，对于K-Means而言，寻找出合适的簇中心点是一个NP-hard问题[10]，无法在多项式时间内计算出全局最优的解。除了随机初始化聚类中心点，研究者们提出了不同的初始点选择策略以降低算法复杂度，旨在有限的迭代次数内提高传统聚类结果质量。然而，当前提出的平衡聚类算法时间复杂度普遍较高，在较大规模数据集上的平衡聚类存在效率较低的问题，Malinen等[11]提出的平衡聚类算法时间复杂度为O(tN3)，Liu等[12]提出的平衡聚类算法时间复杂度为O(tN2)，其中，t为算法迭代次数，N为数据集中的数据总数。

由于现在许多应用场景下的数据集规模较大，需要一种更高效的算法来应对较大规模数据集场景下的平衡聚类任务。针对平衡聚类算法中的这些不足，本文研究中发现，先通过初始点选择算法选择初始点，随后在使用基于贪心的方法聚类同时约束簇的均衡度是一个有效降低平衡聚类算法复杂度的方法。

本文的主要贡献如下：

1) 提出了一种基于贪心策略的平衡聚类算法(Balanced Clustering based on Greedy Strategy, BCGS)用来分配每个数据点，在真实数据集上实施对比实验发现该算法保证了聚类结果的平衡性；

2) 提出了适用于BCGS的一种基于模拟退火的初始点选择算法(Simulated Annealing Clustering Initialization, SACI)用于聚类初始点选择，一系列聚类实验结果表明该方法能够高效地定位出合适的聚类初始点，同时与其他平衡聚类算法相比降低了平衡聚类算法的时间复杂度；

3) 在6个UCI真实数据集和2个公开图像数据集上与其他算法比较了三项聚类评价指标(包括一项平衡性)，实验结果表明本文提出的平衡聚类算法相比其他平衡聚类算法更加高效，而且能够保证聚类结果的平衡性。

1 相关工作

目前已有的平衡聚类可以分为2大类，分别是硬平衡聚类与软平衡聚类。硬平衡聚类是通过对聚类结果中每个簇规模进行严格限制来达到平衡聚类的目的。例如，ConstrainedK-Means Clustering方法中通过对簇中元素个数设置下限来避免在算法执行过程中产生过小的簇[13]； BalancedK-Means[11]是在ConstrainedK-Means Clustering方法上的改进，在聚类开始阶段先构造一个由N个数据点以及N个slot构成的二部图，将N个slot进行K等分形成K个组，在数据点分配阶段，使用匈牙利算法[14]将N个数据点绝对均衡地分配到N个slot中，slot中的每个组即对应结果中的一个簇，该算法的时间复杂度为O(tN3)。

软平衡聚类仅将聚类结果的平衡性作为其中一项约束条件，相较于硬平衡聚类，其对于平衡的约束往往贯穿算法但绝对的平衡状态只作为算法的理想目标并不需要必须达到。在Banerjee等[15]的工作中，他们设计了一个由三个步骤组成的平衡聚类算法，在数据点分配阶段将每个簇中已有数据个数纳入数据点加入簇的代价计算公式中，另外算法基于stable marriage problems问题的思路解决点分配中的稳定性问题； 在Banerjee等[16]的工作中，算法还可以根据预先设定的阈值对聚类结果的平衡度实现弹性控制； 在Liu等[12]的工作中，根据所设计的平衡性约束条件对聚类结果进行约束，其时间复杂度为O(tN2)。

总体来说，之前提出的平衡聚类算法，无论是硬平衡还是软平衡，算法的时间复杂度普遍较高，算法运行时间较长，随着数据规模的增大，需要一种低复杂度的算法来处理平衡聚类问题。

本文提出的平衡聚类算法属于硬平衡聚类，算法分为两个环节：首先创新性地采用模拟退火的方法在数据集中快速定位出合适的K个点作为平衡聚类初始点； 接着基于K个初始点，通过设置的分配规则贪婪地将其周围最近的点加入簇中直到达到簇的规模上限，在此过程中每个点不需要再重新分配簇，所有簇一次性生成，这与现有的硬平衡聚类算法有较大的不同。

2 问题定义

给定数据集D={xi|i=1,2,…,N}，其中，N为数据集中数据总数。平衡聚类是将数据集D按照预先定义的距离划分为K个簇，每个簇拥有一个中心点共K个中心点C={μj|j=1,2,…,K}。每个簇包含的数据点情况存入CSL={Cl1,Cl2,…,ClK}，其中ClK={xi|i=1,2,…,G}表示第K个簇中所有的数据点。α(CSL)表示平衡聚类对于簇的约束条件，如式(2)所示：

(1)

其中：ρ为簇规模平均值，τ为方差阈值。

平衡聚类优化的目标函数是让每个数据点到其所在簇的中心点距离平均值最小，目标函数如式(2)所示：

minMSE(x1,x2,…,xN,μ1,μ2,…,μK);

(2)

s.t.α(CSL)

其中：φ(xi,μe(i))用于计算数据点xi分配至簇e(i)产生的损失值，μK表示第K个簇的中心，e(i)表示D中第i个数据点被分配到的簇。

3 基于模拟退火的平衡聚类初始点选择

K-Means计算每个簇的中心点是一个NP-Hard问题[10]，初始点的计算对算法效果有较大影响。由于本文所提出的平衡聚类算法也是基于传统K-Means，因此如何计算平衡聚类初始点也是算法面临的一个问题。

传统K-Means等聚类算法的迭代终止条件通常为每个数据点到其所在簇中心距离的平均值达到最小，如式(3)所示:

(3)

或者对于前后两次迭代，中心点变化趋于稳定，对于第一种终止条件，由于传统聚类对于每个簇的规模都没有限制，因此，较小的代价函数值很可能是在较为不平衡的簇分布情形下得到的，即数据的局部分布密度会对传统聚类算法中心点的选择以及簇的平衡性有较大的影响。

针对上述提出的初始点选择面临的问题，本文提出了SACI算法，该算法基于模拟退火选择聚类初始点。为了让选择的初始点形成的簇满足平衡的约束条件，对式(4)中每个簇包含的数据个数进行约束，让所确定的中心点到簇中所有Z个点的距离之和最小，如式(4)所示:

(4)

s.t. ∀j∈{1,2,…,K}, ‖Clj‖=N/K-1

其中Z=N/K-1为理想平衡状态下每个簇包含的数据点个数。

由于从数据集中选择出K个中心点并最小化式(4)过程与传统K-Means相似，因此需要一种适用于高效解决该问题的可行方法，否则算法效率将由于较低而无法应对实际应用场景下的平衡聚类问题。

本文所提出的SACI算法采取近似算法的思想来提高聚类初始点选择效率，在计算机科学与运筹学中，近似算法经常与解决NP-Hard问题关联起来，它可以找到合理的解决方案并且相当快速。

首先定义状态集合ζ={ui|i=1,2,…,h}，其中ui表示ζ中的每个状态，即对应不同的初始点选择方案N(ui)表示在状态ui一定邻域内的其他状态且N(ui)⊂ζ。模拟退火中参数T表示当前温度并且单调递减，te为温度下限。

(5)

目标函数用于计算每个状态的得分(这里为式(4))。另外，对于一个给定的K个初始点选择状态U0，假设其在第s次实验后K个初始点选择状态为Us，并在尝试第s+1次实验结束后新状态为Us+1，计算Us与Us+1的目标函数差E(Us+1)-E(Us)，根据目标函数差判断新状态是否被接受。常用的接受准则是Metropolis准则：若E(Us+1)-E(Us)<0则接受新状态Us+1，否则算法依据概率ps接受邻域内的新状态Us+1，即：

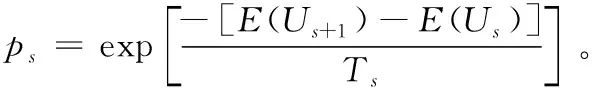
模拟退火依据一定的概率来决定是否接受每次的调整，具有渐进收敛性[16]，不仅可以避免算法陷入局部最优解也可以快速收敛到一个接近全局最优解的初始点集合。

为了更好地描述基于模拟退火的平衡聚类初始点选择算法，现对算法中函数与参数进行介绍。E(x1,x2,…,xN,μ1,μ2, …,μK)对应于式(4)的目标函数的计算过程，ts为退火过程初始温度，te为退火温度下限，T为当前温度，b为退火算法降温速率，TC={xj|j=1,2,…,K}为所有中心点一次调整后新的待选中心点集。本文提出的SACI算法如算法1所示。

算法1 SACI算法。

输入 数据集D，簇数目K，退火初始温度ts，温度下限te，降温速率b；

输出 中心点集C。

1)

C=∅，SD=∅；

2)

T=ts；

3)

从数据集D中随机选择K个点加入C，SD=D，D=D-C

4)

每个簇从D中将与其欧氏距离最近的Z个点加入簇；

6)

while (T>te) do

7)

调整中心点，得到待选中心点集TC；

9)

Δ=nscor-pscor；

10)

企业的运营逻辑是将生产要素转化为商品，通过与市场对接这部分商品会被转化为货币，利用这些货币企业可重新购置生产要素。由此可见，企业的运营依赖于要素流转，当流转效率提高时，企业的收益也将相对提升。但企业在合并重组后，管理机制与资源配置模式会发生改变，在磨合的过程中其要素流转效率将有所降低。资金是计量生产要素的主要工具，因此生产要素流转必然伴随着资金流动。有鉴于此，流转效率的下降也必然会降低资金的使用效率。

ifΔ<0

11)

C=TC，pscor=nscor，D=SD，D=D-C，每个簇从D中将与其欧氏距离最近的Z个点加入簇；

12)

else

13)

λ=random()；

15)

16)

T=b×T；

17)

end while

18)

returnC

算法1中第7)行调整中心点的目的是在每个已确定的中心点“附近”选择某个点作为新的备选中心点。为了让算法能够具有更好的拓展性，而不是具体地严格要求调整至距离最相近的第几个点，针对每个中心点，本文提出了一种中心点选调策略，可以保证新的中心点在原始中心点不远处且较大概率与中心点很靠近。具体地，对于每个簇，随机选择簇中Z/3个数据点并记录下与中心点的距离，从这部分点中选择其距离最近的点作为该簇的新候选中心点。

4 基于贪心策略的平衡聚类

基于第3章所描述的初始点选择算法所选择出的K个初始中心点，本文提出了BCGS算法，算法包括三个步骤:

在第一个步骤中，根据数据点与每个中心点的距离将与每个簇最接近的一部分点首先加入相应的簇中，代价函数如式(6)所示：

Le(xi,μj)=‖xi-μj‖2;xi∈CLj

(6)

第二个步骤中，在决定数据点是否加入某个簇中时不仅考虑与每个簇中心点的距离，同时还考虑了每个簇目前的规模，代价函数如式(7)所示：

Lt(xi,μj)=‖xi-μj‖2/e×‖rj‖，xi∈CLj

(7)

其中‖rj‖表示第j个簇中已有的数据点数目。

在前两个步骤完成时，数据集中的绝大部分数据已经分配至相应的簇中。在第三个步骤时，只考虑每个簇中已有数据个数来决定将数据点添加至哪个簇中，代价函数如式(8)所示：

Lr(xi,μj)=‖rj‖;xi∈CLj

(8)

其中算法的三个步骤对平衡的约束逐渐加强。

为了更好地描述基于贪心策略的平衡聚类算法，现对算法中的参数与相关函数进行介绍：μj表示第j个簇的中心，xi表示每个簇中除中心点外第i个点，Le(xi,μj)表示上述步骤1中计算数据点与簇中心点之间的欧氏距离；Lt(xi,μj)代表上述步骤2中在对簇的平衡性有一定的约束情况下计算点添加至某个簇中的代价；Lr(xi,μj)表示上述步骤3中将剩下的某个数据点作为新点加入某个簇的代价值; 参数p表示在第1个环节中每个簇的生成比率; 参数q表示所设簇之间规模的方差阈值。

算法2 BCGS算法。

输入 数据集D，簇数目K，中心点集C；

输出 簇集合W。

1)

W=∅，M=N；

2)

forj← 1 toKDO

3)

fori← 1 toMDO

4)

计算Le(xi,μj)存入T；

5)

ST=sort(T)；

6)

将ST中的前p×Z个数据点加入第j个簇Wj中；

7)

重新计算第j个簇的中心点；

8)

M=M-p×Z，T=∅；

9)

fori← 1 toMDO

10)

forj← 1 toKDO

11)

计算Lt(xi,μj)存入T；

12)

将xi添加至T中最小值所指的簇Wx；

13)

M=M-1，T=∅；

14)

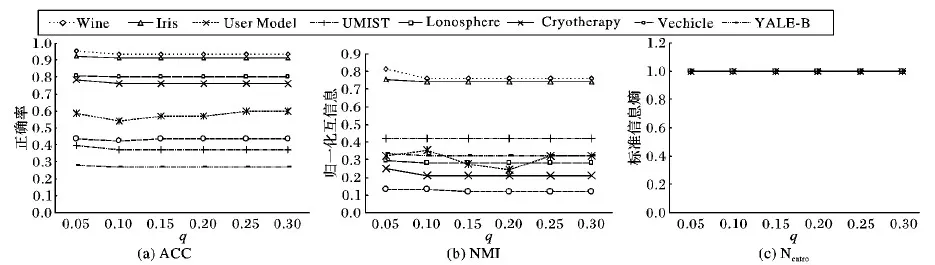
ifα(CSL)

15)

break；

16)

fori← 1 toMDO

17)

forj← 1 toKDO

18)

计算Lr(xi,μj)存入T；

19)

将xi添加至T中最小值所指的簇Wx；

20)

M=M-1，T=∅；

21)

returnW

其中，第7)行中所述的重新计算中心点方法即将簇中所有点坐标相加取算数平均值获得。

5 时间复杂度分析

本文提出的平衡聚类算法包括计算初始中心点与平衡聚类2个步骤，在初始点计算算法的每一次迭代中，计算除中心点以外的每个数据点与每个中心点的距离，时间复杂度为O(N)，随后每个中心点依次将距离每个簇中心最近的Z个数据点加入到相应的簇中。取距离最近Z个点加入到簇中需要对距离排序，本文使用归并排序对其进行排序，归并排序算法在最坏情况下的时间复杂度为O(NlogN)，因此模拟退火选点算法时间复杂度为O(tNlogN)。

在第二个步骤中，算法的第1个环节需要计算每个中心点最近的p×Z个数据点，其中涉及一次排序，使用归并排序的时间复杂度为O(NlogN);在第2个环节中需要计算剩下的数据点加入每个中心点的代价，时间复杂度为O(N);在第3个环节中，依次将剩余的极少数数据点加入当前规模最小的簇中，时间复杂度为O(N),因此,贪心平衡聚类算法时间复杂度为O(tNlogN)。在前面分析过，初始中心点选择算法单次迭代时间复杂度也为O(tNlogN)，因此本文所提出的平衡聚类算法的时间复杂度为O(tNlogN)。

6 实验与分析

本章中在6个UCI真实数据集与2个公开图像数据集上将提出的平衡聚类算法与其他五种聚类算法相比较，分别是K-Means、FCM、Spectral Clustering (SC)、BalancedK-Means、BCLS(Balanced Clustering with Least Square regression)。其中K-Means与 FCM是2种经典的聚类算法;K-Means是很典型基于距离的聚类方法，采用距离作为相似性的评价指标，把得到紧凑且独立的簇作为最终目标; FCM是一种无监督的模糊聚类方法，该算法是基于对目标函数的优化基础上提出的一种聚类方法，常用于模式识别中; SC算法建立在谱图理论基础上，其本质是将聚类问题转化为图的最优划分问题，能在任意形状的样本空间上聚类且收敛于全局最优解; BalancedK-Means是一种硬平衡聚类算法，通过在由节点与slot组成的2部图上使用匈牙利算法进行簇分配，可以将数据点绝对平衡地分配到所有簇中去; BCLS是一种基于对平衡聚类目标函数优化基础上提出的一种高效平衡聚类算法。

6.1 实验设置

6.1.1 数据集与预处理

本实验选取了6个UCI真实数据集与2个公开图像数据集，分别是Wine、Lonosphere、Iris、Cryotherapy、User Model、Vechicel、UMIST、YALE-B。为了更好地测试每个算法的平衡聚类性能，将所有数据集中每种类别的数据个数删减至相同，即在平衡的数据集下聚类测试聚类结果的均衡度，所有算法运行20次，取目标函数值最低的结果，这与文献[12]中的实验设置类似。调整后的每个数据集信息如下：Wine中数据总数144，包含3类；Lonosphere中数据总数252，包含2类；Iris中数据总数150，包含3类；Cryotherapy中数据总数84，包含2类；User Model中数据总数200，包含4类；Vechial中数据总数796，包含4类，UMIST总数据数380，包含20类；YALE-B总数据数2 204，包含38类。为了提高实验效率，将维度较高的数据集UMIST与YALE-B使用主成分分析(Principal Component Analysis, PCA)进行了降维处理，保留95%的信息。

6.1.2 评价体系

使用平衡聚类常用的三种评价方法对提出的方法进行评估，包括：

1) 聚类准确率(Accuracy，ACC)[17]。该指标衡量数据所有数据元素在聚类后的标签相较于先验知识中真实标签的准确率，如式(9)所示:

(9)

其中:N为数据集中元素总数，若si=map(ri)，值为1，否则为0; map()为一个映射函数，将聚类结果的数据标签映射至原数据集中相应的标签。

2) 归一化互信息(Normalized Mutual Information，NMI)[18]，用于评价聚类结果与数据集原分布近似程度，如式(10)所示:

(10)

其中：I(X,Y)表示分布X与Y的互信息，H(X)表示分布X的信息熵。

3) 标准信息熵(Normalized Entropy, Nentro)[12]，用于衡量簇之间的平衡度，值越接近1表示所有簇之间越平衡，计算公式如式(11)所示：

(11)

其中rk表示第K个簇中的数据点个数。

6.2 实验结果与分析

实验中每个算法的聚类结果质量及其平衡性如表1所示，主要的对比结果如下：

1) 对于规模或簇数目较小的数据集，实验结果表明，本文提出的平衡聚类算法不仅能够获得更加平衡的聚类结果，同时聚类结果的准确率与标准化互信息也普遍比其他算法要高。相较于BalancedK-Means、BCLS这两种聚类结果平衡性较好的算法，BCSG在每个数据集上的聚类结果准确率相比BalancedK-Means平均提高了4个百分点，归一化互信息也平均提高了4个百分点，BalancedK-Means由于是一种硬平衡聚类算法，因此聚类的结果可以每次都达到绝对的平衡；相比BCLS准确率平均提高了3个百分点，归一化互信息也平均提高了1个百分点，而在传统的聚类算法上，BCSG结果的平衡性属于最高；另外，只有在少数数据集上其他算法的准确率与

归一化互信息比BCSG高。

2) 对于规模或簇数目较大的数据集，实验结果表明，本文提出的平衡聚类算法依然能够保持聚类结果很好的平衡性，同时聚类结果也具有较高的准确率与归一化互信息，准确率和归一化互信息与BalancedK-Means相近。其中，BCLS由于是一种基于对目标函数优化的平衡聚类算法，在数据集规模或者簇数目过大时，聚类结果的平衡性会有所降低。BalancedK-Means由于其时间复杂度过高，在大规模数据集上的运行效率较低，如表1所示，BalancedK-Means在数据集YALE-B上较长时间内未得出聚类结果。另外，由于SC算法考虑数据集的全局分布，因此在较大规模数据集上聚类结果的准确率与归一化互信息相较于其他算法会较高。

接下来的实验主要关注不同聚类方法的时间性能，主要结果如表2所示。在真实的6个UCI数据集与2个公开图像数据集上平衡聚类实验，实验结果表明，本文提出的BCSG算法运行时间比其他两种性能较好的平衡聚类算法BalancedK-Means与BCLS都短，其中BalancedK-Means的运行时间最长，BCLS其次，在较大规模的数据集上(YALE-B)运行时间最高减少了40%，BalancedK-Means较长时间内未能计算出结果，BCSG算法具有更好的时间性能。

表1 六种聚类算法在八个数据集上的实验结果

注：“—”表示算法在较长时间内未能得出聚类结果。

表2 三种算法实际运行时间对比 s

为了验证初始点选择算法对算法结果的影响，实验设计将本文提出的BCSG算法使用不同的初始点选择算法进行对比，分为随机取初始点与基于模拟退火取初始点，在6个UCI数据集与2个图像数据集上的聚类结果如表3所示，实验结果表明，虽然使用不同的初始点选择算法对聚类结果的平衡性影响非常小，但对聚类结果的准确率与归一化互信息具有较大的影响； 因为BCSG算法中的贪心聚类环节主要用于约束簇的平衡度，初始点选择算法在于选取出准确的中心点使得簇分布与数据真实情况相近。实验进一步验证了BCSG算

法中两个环节的有效性。

图1给出了不同p值对于不同聚类评价指标的影响。从图1可以看出，算法2中的参数p影响平衡聚类的结果质量，其中，参数p对归一化互信息(NMI)有较大影响，对正确率(ACC)的影响较小，对标准信息熵(Nentro)影响非常小。

图2给出了不同q值对于不同聚类评价指标的影响。从图2可以看出，算法2中的参数q也影响平衡聚类的结果质量，除个别数据集外，对准确率(ACC)与归一化信息(NMI)的影响都较小，对标准信息熵(Nentro)影响非常小。

表3 不同初始点选择算法对聚类结果的影响

图1 p的不同取值对不同聚类评价指标的影响

图2 q的不同取值对不同聚类评价指标的影响

7 结语

为了提高现有平衡聚类算法的聚类效果与时间性能，本文提出了一种低时间复杂度、高效的平衡聚类算法，该算法采用模拟退火策略在数据集中首先快速找到合适的平衡聚类初始点，模拟退火作为一种近似算法可以在较短时间内获得NP-Hard问题的一个高质量的解决方案代替最优解，降低了算法的时间复杂度。接着，基于模拟退火选择出的初始点，算法使用贪心的策略形成K个簇，具有较低的时间复杂度，在6个UCI真实数据集与2个公开图像数据集上实施对比实验的结果表明，本文提出的BCSG不仅比其他平衡聚类算法高效，而且能够保证聚类结果的平衡性。在之后的工作中，可能将平衡聚类应用于分布式数据库的节点数据分配任务中。