空间几何中的探索性问题的求解策略

■齐展修 胡 磊

立体几何中的探索性问题一般都是条件开放性的探索性问题,一般采用的方法是执果索因,先猜后证的方法,即观察与尝试给出的条件再证明,或者假设求解的结果存在,寻找使得这个结论成立的条件,把几何问题转化为代数问题来解决,如果找到符合题目结果要求的条件,则存在;如果找不到符合题目要求的条件或出现了矛盾,则不存在。

一、平行中的探索性问题

例1 如图1所示,已知菱形AECD的对角线AC,DE交于点F,点E为AB的中点。

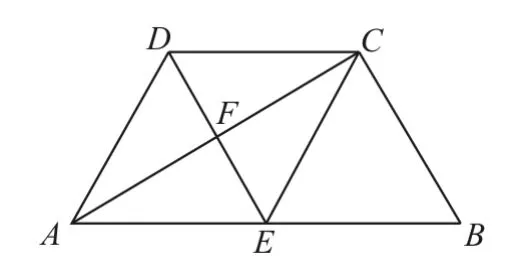
图1

将三角形ADE沿线段DE折起到PDE的位置,如图2所示。

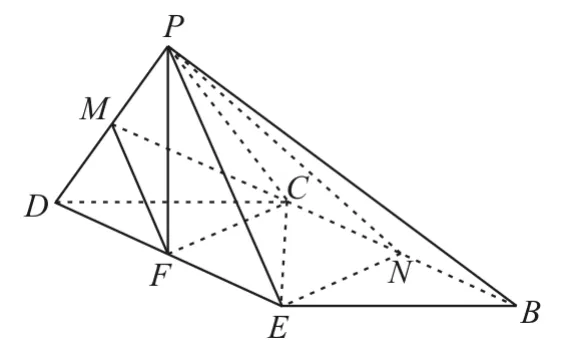
图2

(1)证明:DE⊥平面PCF。

(2)证明:平面PBC⊥平面PCF。

(3)在线段PD,BC上是否分别存在点M,N,使得平面CFM∥平面PEN?若存在,请指出点M,N的位置,并证明;若不存在,请说明理由。

解：(1)折叠前,因为四边形AECD为菱形,所以AC⊥DE。折叠后,DE⊥PF,DE⊥CF。

又PF∩CF=F,PF、CF⊂平面PCF,所以DE⊥平面PCF。

(2)因为四边形AECD为菱形,所以DC∥AE,DC=AE。

又点E为AB的中点,所以DC∥EB且DC=EB,可知四边形DEBC为平行四边形,所以CB∥DE。

由(1)得DE⊥平面PCF,所以CB⊥平面PCF。又因为CB⊂平面PBC,所以平面PBC⊥平面PCF。

(3)存在满足条件的点M,N,且M,N分别是PD和BC的中点。

又EN、PE⊂平面PEN,PE∩EN=E,MF、CF⊂平面CFM,MF∩CF=F,所以平面CFM∥平面PEN。

本题考查线面垂直、面面垂直的证明,考查满足条件的点的位置的确定,考查空间中的线线、线面、面面之间的位置关系等基础知识。

二、垂直中的探索性问题

例2 如图3所示,在长方体ABCDA1B1C1D1中,AB=1,AD=2,E,F分别为AD,AA1的中点,Q是BC上一个动点,且BQ=λQC(λ＞0)。

图3

(1)当λ=1时,求证:平面BEF∥平面A1DQ。

(2)问是否存在正数λ,使得BD⊥FQ。若存在,请求出λ的值;若不存在,请说明理由。

解：(1)当λ=1时,Q为BC的中点。

因为E是AD的中点,所以ED=BQ,ED∥BQ,则四边形BEDQ是平行四边形,所以BE∥QD。

又因为BE⊄平面A1DQ,DQ⊂平面A1DQ,所以BE∥平面A1DQ。

因为F是A1A的中点,所以EF∥A1D。因为BF⊄平面A1DQ,A1D⊂平面A1DQ,所以EF∥平面A1DQ。

又因为BE∩EF=E,EF⊂平面BEF,BE⊂平面BEF,所以平面BEF∥平面A1DQ。

(2)因为A1A⊥平面ABCD,BD⊂平面ABCD,所以A1A⊥BD。由于BD⊥FQ,A1A、FQ⊂平面A1AQ,所以BD⊥平面A1AQ。

因为AQ⊂平面A1AQ,所以AQ⊥BD。在矩形ABCD中,由AQ⊥BD,可得△AQB∽△DBA,所以AB2=AD·BQ。

本题考查面面平行的证明,考查两线段比值的求法,考查空间的线线、线面、面面之间的位置关系,考查空间想象能力,考查化归与转化思想和数形结合思想的应用。

作者单位：山东省平邑县第一中学(西校)