基于髋关节正位X线片可测量髋臼假体方位

李 栋，苏秀云，王华琼，孙大炜，赵 鹏，范德森，张 健，蒋 兴

1广州和平骨科医院，广东 广州 510315；2解放军第307医院骨科，北京 100071；3广东省第二人民医院创伤外科，广东 广州 510317

髋臼假体的方向既是影响全髋关节置换术后肢体功能的重要因素，又是评价手术质量的重要指标，髋臼假体的方向可用手术学前倾角和倾斜角、解剖学前倾角和倾斜角、放射学前倾角和倾斜角三对角度定义，三对角度之间可以通过数学公式相互推导[1]。放射学前倾角和倾斜角是临床中最常使用的评价指标，而放射学前倾角的正常范围争议最大，有些学者建议0°～30°，有些则认为10°以内太小，而30°则太高[2]。很多学者对放射学前倾角的测量方法都是基于髋臼或骨盆的正位X线片进行的，主要包括Lewinnek[3]、Widmer[4]、Pradhan[5]、Ackland[6]、Hassan[7]、Liaw[8]、Fabeck[9]和Kosiyatrakul[2]、Bachhal[10]等方法。有学者是基于特殊侧位髋关节X线片，如Woo-Morrey[11]。也有学者直接基于髋关节CT扫描进行测量[12-14]。CT测量需要精确的定义测量参考平面，而相关方法并不一致，且存在费用高昂，射线暴露剂量大等缺点。因此基于X线片的测量方法仍然是研究热点。

本研究基于全髋置换术后的髋关节正位X线片测量髋臼假体的放射学前倾角和倾斜角，采用椭圆拟合方程，基于最小二乘法通过选择若干标记点拟合出臼杯的开口椭圆，利用编写的程序计算出臼杯开口椭圆的长短轴，并计算出放射学前倾角和倾斜角，最后进行信度实验评价本方法的观察者间及观察者内信度。

1 资料与方法

1.1 基本资料

选择在307医院进行全髋关节置换术的34例病例，其中男13例，女21例，平均年龄58.38岁，左侧20例，右侧14例。术前诊断为：股骨颈骨折11例，股骨头坏死16例，骨性关节炎3例，类风湿性关节炎3例，先天性髋关节发育不良2例。全髋关节置换术后X线片均为术后2～7 d完成。通过医院的PACS系统获取X线片进行测量。

1.2 原则分析

由于髋臼假体前倾角测量的基础是尽可能标准的将臼杯开口拟合为椭圆，并根据数学基础知识计算出椭圆所在平面与投影平面（冠状面）之间的夹角。因此，首先建立椭圆切线方程（椭圆一次导数）及切线变化率方程（椭圆二次导数），利用Mathematica软件做函数图，并据此分析判断椭圆拟合点的最佳选点方法。

1.3 测量方法

（1）根据髋臼假体前倾角θ=arcsin（椭圆长轴a/椭圆短轴b），编写Matlab软件计算程序；（2）将髋关节正位X线片依次导入Matlab软件；（3）基于最小二乘法，利用Matlab软件的椭圆拟合程序（http://www.mathworks.com/matlabcentral/fileexchange/3215-fitellipse），在臼杯的开口上选择拟合点；（4）Matlab软件自动输出拟合出的椭圆的长短轴，利用自编程序计算出椭圆平面与屏幕所在平面（冠状面）之间的夹角，即髋臼假体前倾角，和臼杯长轴与身体纵轴之间的夹角，即髋臼假体倾斜角。

1.4 信度实验

组内相关系数（ICC）检验本测量方法的观察者间及观察者内信度。为评价观察者间信度，由3名医生以随机顺序独立完成所有X线片前倾角和倾斜角的测量；为评价观察者内信度，由另外1名医生重复3次所有数据的测量，每次均以随机顺序进行，且2次之间间隔至少1 d。

计算ICC之前，为避免测量组内带来的误差，用重复测量方差分析计算测量组内的均方。根据Landis-Koch标准，ICC值0～0.2为微弱，0.21～0.40为一般；0.41～0.60为中等，0.61～0.80为较强，0.81～1.0为完美。

1.5 统计学分析

对数据进行方差齐性检验后，利用SPSS 20.0对所有数据进行统计学分析，P＜0.05为差异有统计学意义。

2 结果

2.1 椭圆拟合选点原则

由于所需拟合的椭圆的长短轴均未知。在假定长轴确定的情况下，以长轴a为X轴，短轴b为Y轴，中心为原点，根据椭圆公式计算椭圆第一象限的切线方程，即椭圆的一阶导数，在此基础上进一步推导出第一象限切线的斜率随X轴增加的变化率，即椭圆的二阶导数，假定长轴a=5，短轴b=1.3，前倾角=15°。二次导数利用Mathematica软件做函数图（图1A）。反之，假定短轴已确定，以短轴为X轴，长轴为Y轴，计算椭圆第一象限的二阶导数。假定短轴b=1.3，长轴a=5，前倾角=15°。二次导数利用Mathematica软件做函数图（图1B）。

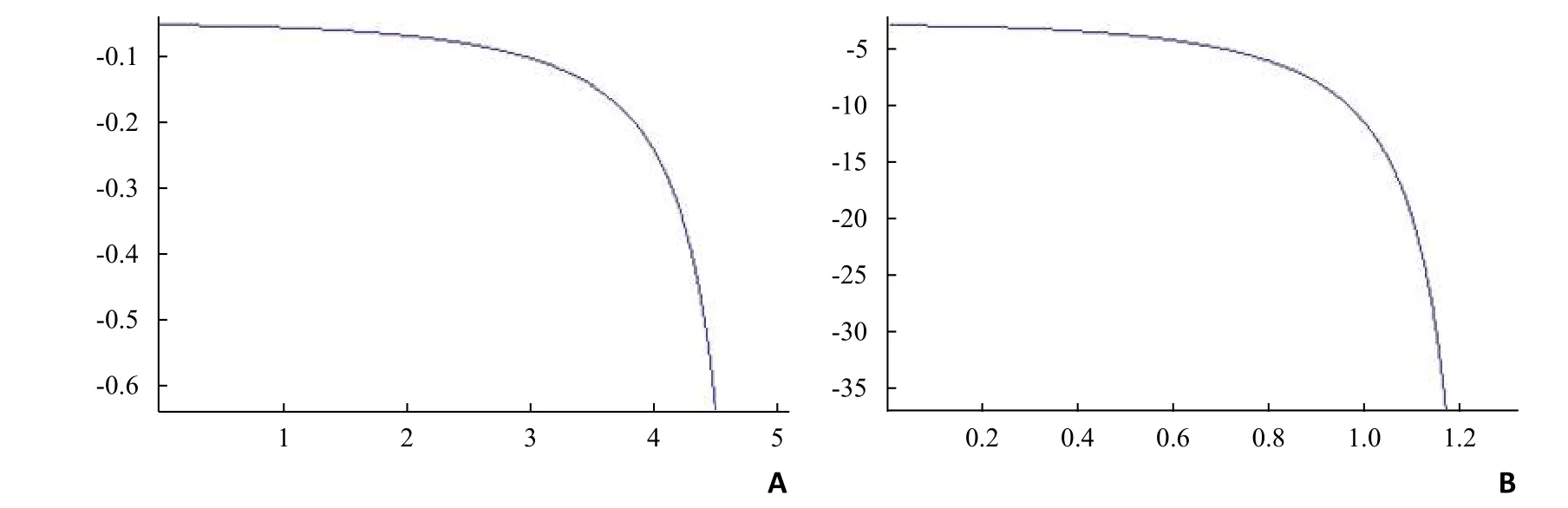
图1 椭圆二次导数的函数图

由上述两副函数图可知，可知随X轴的增大，椭圆切线斜率的变化率也随之增大。因此距离长短轴端点越近，椭圆切线变换率越小，在长短轴端点附近选择拟合点对拟合椭圆形态的影响也最小；距离长短轴端点越远，椭圆切线变换率则越大，选择拟合点对拟合椭圆形态的影响也最大。因此，椭圆拟合点应为尽量靠近椭圆长轴和短轴的两端（图2）。模拟出髋关节置换术后正位像（图3），臼杯及股骨头假体（图4、5）。

图2 靠近椭圆长轴和短轴的两端选择椭圆拟合点

2.2 前倾角及倾斜角测量信度实验

观察者内信度结果为：前倾角和倾斜角的组内相关系数ICC分别为0.916（95% CI：0.858～0.954）和0.948（95% CI：0.910～0.972），测量组的组内均方分别为4.435，74.411（P＞0.05）。观察者间信度结果为：前倾角和倾斜角的组间相关系数ICC分别为0.893（95%CI：0.821～0.941）和0.937（95% CI：0.892～0.966），测量组的组内均方分别为1.761，0.352（P＞0.05）。

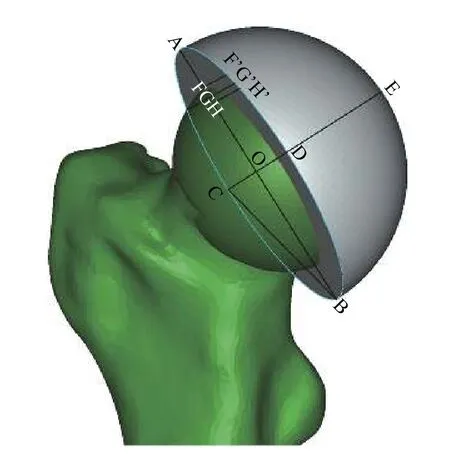
图3 模拟出的髋关节置换术后正位像

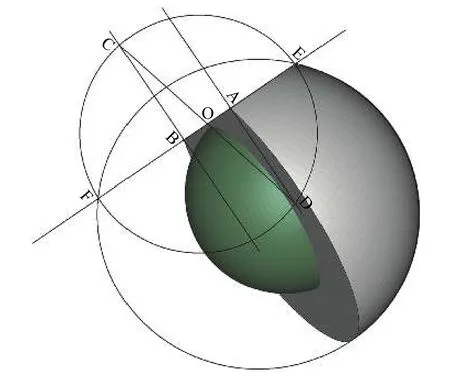
图4 半球为模拟出的臼杯，球为模拟出的股骨头假体

图5 垂直于EF平面方向观察被EF平面切割后的臼杯

3 讨论

以往测量髋臼假体方位的方法，大多是基于髋臼的正位X线片，通过一些特殊的测量工具、数学运算或基本的立体几何知识完成所需测量。其数学原理均是基于臼杯开口在X线正位片的投影为一椭圆这一几何概念，而臼杯开口平面倾斜的角度即为放射学前倾角θ，等于arcsin（椭圆短轴b/椭圆长轴a）。这一方法最早是由McLaren[15]使用，Lewinnek和Pettersson[16]分别于1978年和1982年也发表了同样的方法。此后，很多学者基于这一公式开发了不同的测量方法。

Marx[17]认为Widmer[4]的方法最为准确。Haenle[18]认为改良后的Pettersson[16]方法更准确。Nho[19]认为Lewinnek[3]、Hassan[7]、Liaw[8]等的方法比较准确，Widmer[4]和Ackland[6]的方法则欠佳。Nomura[20]认为Widmer[4]的方法比较准确。由此可见，尽管以往的方法被反复比较和研究，仍然没有一致性结论。实际上以往的方法之间存在等式关系，下面的推导过程可以帮助我们找出其间的相关性并进一步寻找更好的测量方法。

Liaw[8]直接测量出长轴AB与长轴顶点B和短轴顶点C连线BC之间的夹角，即tan∠OBC=OC/OB，则θ=arcsin（OC/OB）=arcsin（tan∠BAC）。Ackland的方法需要利用椭圆方程其中a和b分别为长短轴。假设以长轴为X轴，短轴为Y轴，以椭圆中心为圆心建立直角坐标系，做垂直于长轴的任意垂线GG’，GG’与椭圆相交于点G’，则G’的坐标为（OG，GG’）。带入椭圆方程可求出短轴θ=arcsin（b/a）=arcsin（GG ’/Pradhan和Hassan的方法与Ackland的相似，只不过指定了不同长度的OG。Pradhan将G定义为长轴1/5处一点，则G’的坐标为（0.15a，GG’），带入椭圆方程可以得b=2.5GG’，即θ=arcsin（b/a）=arcsin（GG’/0.4a）。Hassan选择没有被股骨头遮挡的一点指定为F，再进行与Ackland相同的计算过程。Pradhan和Hassan的方法还能用立体几何的知识，通过视角变化推导，过程和Kosiyatrakul的相同。可见，在长轴确定的情况下，Liaw、Ackland、Pradhan和Hassan的方法的差异仅在于选择椭圆长轴两侧的边界点的不同，而这也是这几种方法测量误差的主要来源。

许多方法都有一个前提，那就是假定臼杯假体为一个半球形[4，9-10，21]。那么随着臼杯的倾斜，臼杯中心即椭圆中心距离半球顶点的距离OE始终为椭圆长轴的一半，Widmer的方法是基于骨盆的X线正位片，由于拍摄骨盆X线正位片时，X线管球并非正对髋关节中心，而传统的计算公式是基于髋关节正位X线片的，因此需要在传统的公式后加一个校正系数。

Fabeck[9]、Kosiyatrakul[21]和 Bachhal[10]的测量方法的推导过程都需要利用一些立体几何的基础知识。Kosiyatrakul[21]首先还原了臼杯的完整球形，再沿臼杯长轴做一平面EF，与椭圆相交于A和B，与臼杯交于E，以AB的中点O为圆心，OE为半径作小圆，分别经过A和B做垂直于平面EF的平面AD和BC，其中C和D分别为平面AD和BC与小圆的交点。那么，∠DCB即为臼杯的放射学前倾角。实际上，上述小圆为垂直于平面EF的方向观察到的被切割的臼杯，平面AD和BC均垂直于冠状面，臼杯长轴与冠状面的夹角也等于臼杯开口平面与平面AD或BC的夹角。Bachhal[10]的方法和Kosiyatrakul[21]的类似，但其省略了还原臼杯完整球形的过程。Fabeck[9]制作了一个特殊的量角器，可以在X线片上直接测量出上述角度。利用相似的办法，只要变换一下椭圆的切割方向，如沿水平面或矢状面切割，就可以测量出投影在水平面或矢状面的解剖学前倾角和手术学前倾角。由此可见，Widmer[4]、Fabeck[9]和Kosiyatrakul[21]的方法的测量区域仅限于椭圆的局部，用局部数据计算完整的椭圆的参数无疑会有误差放大效应。

此外，临床中使用的假体的设计原理并不一致，并非所有臼杯均为半球形结构，因此Widmer[4]、Fabeck[9]和Kosiyatrakul[21]的方法就会受到限制。以上方法均有一个共同的不足，是首先需要人为确定椭圆的长轴，而这也是所有方法的测量误差的一个主要来源。如何基于X线片相对准确的作出臼杯开口椭圆，一些学者尝试使用计算机软件完成这一操作，Lu[22]使用了PACS系统自带的椭圆拟合工具，Liaw[23]也开发了一套测量软件，但以上软件操作的第一步都需要定义椭圆长轴。商业软件TraumaCad也需要先确定椭圆长轴。为了优化椭圆拟合点的选择方法，我们对任一短轴b=1.3，长轴a=5的椭圆作二次导数，并作出二次导数的函数图，希望能找到椭圆拟合点选择的最佳方法。椭圆的一次导数即椭圆上点的切线的斜率，椭圆的二次导数则为椭圆上点的切线的斜率的变化率，也即椭圆上点的方向的变化情况。任何椭圆拟合程序的基础均是选择椭圆拟合点，因此，选择那些方向变化较小的区域的点来拟合椭圆无疑会更加准确。

由于在X线正位片上，短轴和长轴均无法获取，首先假定长轴已确定、短轴未知，再假定短轴已确定、长轴未知，分别研究这两种情况下椭圆上的点的方向的变化情况。由结果可知，离椭圆长短轴端点越近，椭圆的二次导数越小，亦即椭圆上的点的方向的变化越小。基于这一原理，利用Matlab软件的椭圆拟合程序，在不用提前确定长短轴的情况下，尽量靠近长短轴的端点的区域选择椭圆拟合点，基于最小二乘法拟合出所求椭圆，希望能最大程度的减少测量误差。最后利用自行编写的程序直接输出计算出的臼杯前倾角和倾斜角。

为了验证这一测量方法的可靠性，本研究选择了4名骨科医生完成信度实验。其中3名医生各自独立进行1次所有的测量。另一名骨科医生重复进行3次所有的测量。根据Walter和Eliasziw计算信度实验样本量的公式[24]，34例测量对象、3次测量可以满足本实验要求。另外按照Weir[25]的研究，首先对所有测量结果进行重复方差分析，以避免来自测量组内的明显误差。由实验结果可知，本研究采取方法测量的前倾角和倾斜角的组间相关系数和组内相关系数均较高，ICC系数均大于0.9，可用于推广应用。

通过对以往研究的系统回顾，可知以往学者提出的测量髋臼假体方位的方法均存在等式关系。基于椭圆导数理论，本研究提出了一种基于髋关节正位X线片测量髋臼假体方位的新方法，可以用于评价全髋关节置换术后的假体位置，并可用于进一步分析假体位置不良与其他并发症的相关性。