基于激光多普勒频移的钢轨缺陷监测

邢 博，余祖俊,2，许西宁,2*，朱力强,2

(1.北京交通大学 机械与电子控制工程学院，北京 100044; 2.北京交通大学 载运工具先进制造与测控技术教育部重点实验室，北京 100044)

1 引 言

钢轨在生产、焊接、铺设和行车过程中会出现各种不同的伤损。这些伤损的出现，不仅影响行车的平稳性和舒适性，还会危及行车安全。钢轨伤损种类很多，主要包括：疲劳伤损、锈蚀、磨耗、弯曲变形和裂纹等[1]。对于出现在钢轨表面的伤损，可以通过机器视觉的方法来检测[2]。而对于钢轨内部伤损，常规的基于图像的方法无法检测。钢轨内部伤损早期难以发现，在列车运行载荷的反复作用下，这些内部小的缺陷和裂纹会逐渐扩大，甚至发生突然断裂现象，引发严重的行车事故。随着我国铁路事业的发展，钢轨内部缺陷已成为影响铁路运输安全的主要伤损类型。

为了早期发现钢轨内部缺陷，确保对无缝线路长钢轨服役状态的及时掌控，我国铁路相关部门采用定期检测的模式对钢轨进行探伤作业，利用大型探伤车对各条高铁线进行定期巡检，发现疑似伤损时，再采用钢轨探伤仪进行人工复核[3]。大型钢轨探伤车和小型钢轨探伤仪均基于超声波检测技术设计，大型钢轨探伤车速度快，检测效率高，但造价昂贵；小型钢轨探伤仪检测精度高，但速度慢，且这两种检测方式都要占用天窗时间。因此，铁路工务部门迫切需要一种可以实时在线监测无缝线路长钢轨内部缺陷的方法，以实现对无缝线路钢轨服役状态的在线监测，确保高速铁路行车安全。

轨道电路是我国铁路信号系统中的基础组成部分，轨道电路以一段铁路线路的钢轨为导体构成回路，能够完成列车占用检测、断轨检测等功能[4]。基于轨道电路的断轨检测方式，能够最大程度地满足实时在线监测的要求，但是这种方法只能在钢轨完全断裂时给出报警信号，无法检测钢轨内部缺陷。

目前，铁路系统检测钢轨内部缺陷主要采用超声波法[5]，这种方法一般采用高频的超声体波作为信号源，基于这一技术设计的钢轨探伤车，无法实现对钢轨内部缺陷的实时在线监测，因此需要研究一种新的检测技术来实现对钢轨内部缺陷的实时在线监测。当在钢轨中激励低频、高能量的超声波时，超声波在钢轨边界不断发生反射、折射以及纵横波的转换，从而产生了一种新的超声波信号，即超声导波。超声导波特别适合检测横截面一致、距离很长的波导介质材料，如管道、钢轨等[6-7]。由于钢轨具有声导管特性，超声导波在其内部可以传播很远的距离，达到2 km以上。导波的接收方式一般采用超声导波换能器，但此类接触式测量的方法会受到换能器的粘贴位置、粘贴胶质及轨温等因素的影响，大大降低测量结果的准确率。本文采用激光多普勒频移法[8]检测钢轨振动速度曲线，经过信号处理后基于脉冲回波法，通过检测超声导波在钢轨内部缺陷处产生的回波信号，可以实时在线监测钢轨，早期发现钢轨内部存在的缺陷。同时，相对于采用换能器接收导波信号，激光多普勒频移法有良好的线性特性，提高了检测点的时空分辨率，并且对钢轨振动不存在扰动现象，有助于提高检测精度。

2 钢轨中的超声导波

2.1 常规超声导波频散曲线的计算

由于钢轨横截面形状不规则，其内部可传播的导波模态数量很多。基于超声导波技术检测钢轨内部缺陷，首先应该掌握钢轨内部超声导波各模态的基本特性[9-10]。导波频散曲线包含了导波各模态的频率、波数、相速度、群速度、振型等信息，是分析导波传播特性的重要依据。半解析有限元方法(Semi-Analytical Finite Element,SAFE)可以求解钢轨中超声导波的频散曲线[11-12]。以CHN60钢轨为例，半解析有限元方法在求解时，将CHN60钢轨横截面作有限元离散，假定导波沿钢轨纵向以简谐振动的形式传播，基于有限元方法建立波动方程，通过求解特征方程得到特征值和特征向量，进而绘制出CHN60钢轨中超声导波的频散曲线，其中特征值包含了频率、波数信息；特征向量包含了导波各模态的振型信息。

首先建立CHN60钢轨坐标系，如图1所示。

图1 CHN60钢轨坐标系 Fig.1 Coordinates of CHN60 rail

导波波数为ζ，频率为ω。钢轨中每一个质点的位移、应力和应变可以表示为[13]：

u=[uxuyuz]T

σ=[σxσyσzσyzσxzσxy]T

ε=[εxεyεzγyzγxzγxy]T, (1)

其中，εx、εy、εz是正应变，γyz、γxz、γxy是剪应变。在材料的弹性范围内，应力和应变之间满足胡克定律，即：σ=Cε。其中，C为钢轨的弹性模量。

钢轨中任一点的应变和位移的关系用矩阵形式表示为：

(2)

式中

(3)

与传统的有限元方法不同的是，SAFE方法求解CHN60钢轨中传播的超声导波的频散曲线时，首先假定其以简谐波形式沿钢轨纵向传播，因此仅需对钢轨的横截面作有限元离散即可。钢轨中任意离散节点的位移如式(4)所示[11]，其中x为钢轨纵向坐标。

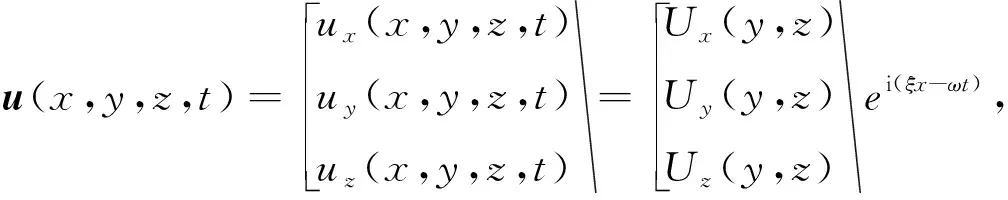
选择三角形单元对CHN60钢轨的横截面作有限元离散，得到177个节点，255个单元，如图2所示。

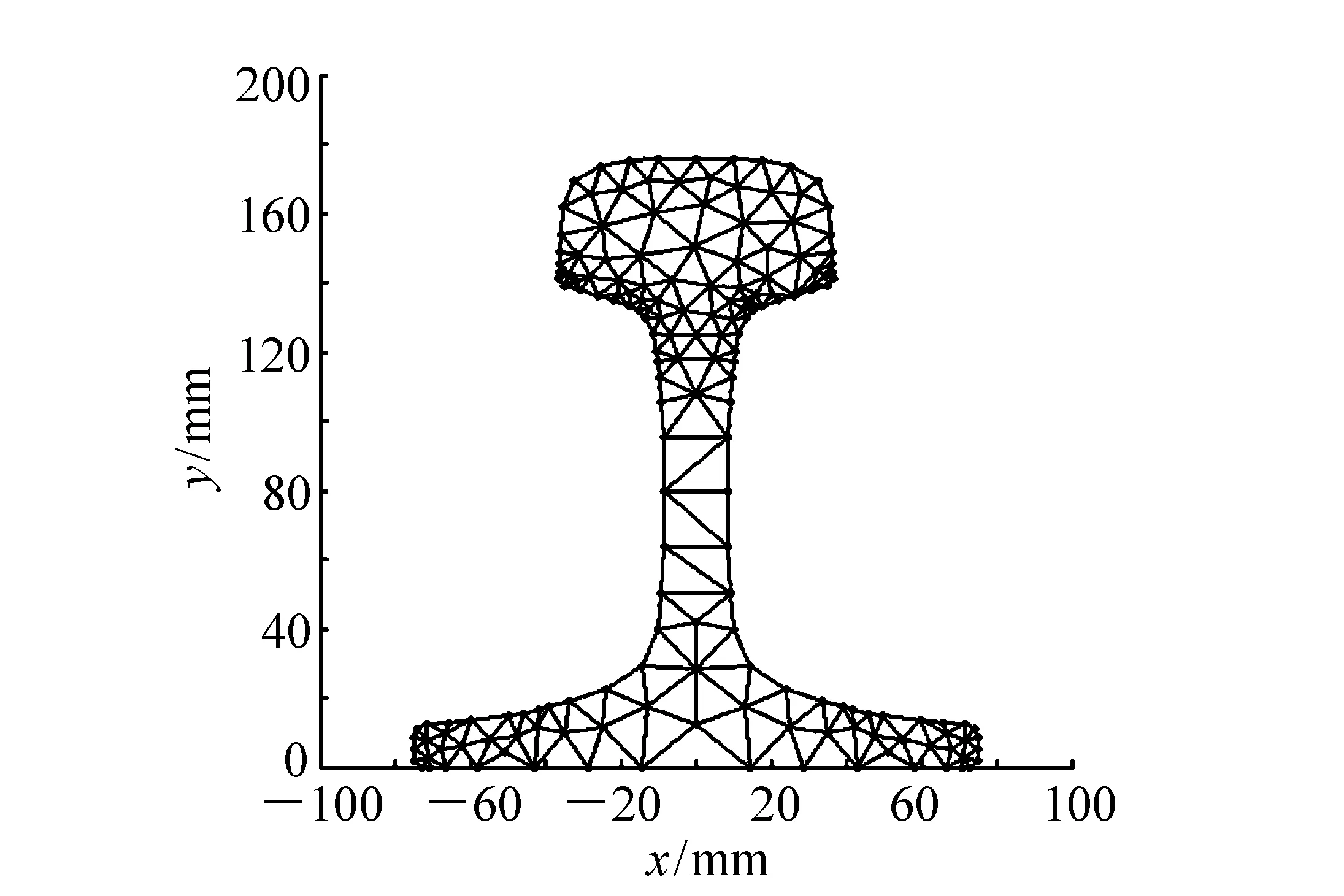
图2 CHN60轨截面离散图 Fig.2 Discretization of cross section of CHN60 rail

钢轨横截面采用三角形单元离散，由离散后的节点位移和单元的形函数可以得到单元内任意质点的位移，单元的应变、应力矢量可通过节点的位移来表示。根据哈密顿原理，同时求解CHN60钢轨中任意一点的应变能和势能，可得到钢轨中导波传播的动力学方程[14]：

[K1+iξK2+ξ2K3-ω2M]MU=0 , (5)

其中，U包含节点在x、y、z三个方向的位移，M为节点质量矩阵，ξ、ω分别为波数和角频率，K1、K2、K3为刚度矩阵。

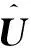
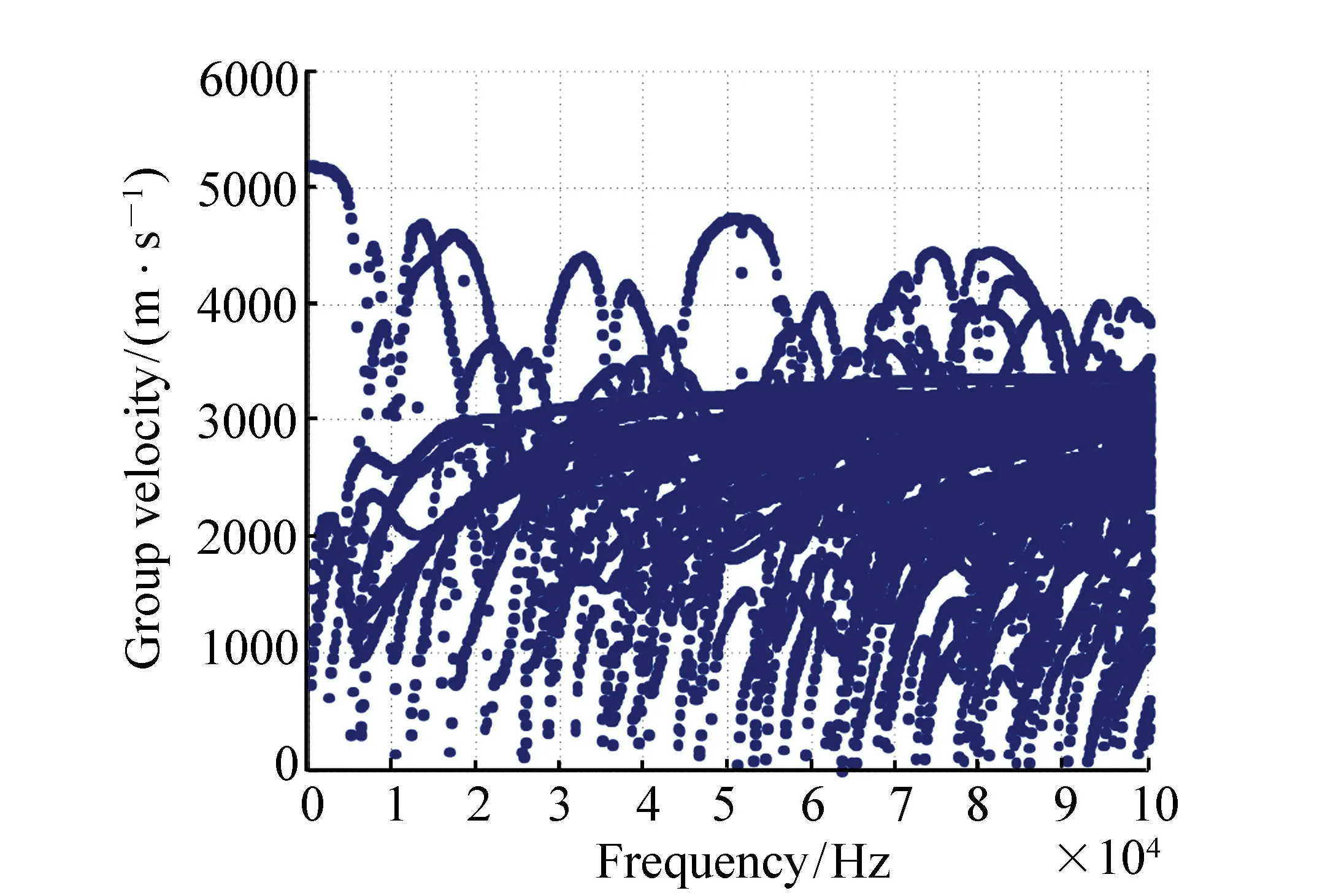
图3 频散曲线(T=32 ℃) Fig.3 Dispersion curves(T=32 ℃)

由图3可知，同一频率下，钢轨有多个可传播的导波模态，且频率越大，导波模态数量越多。

2.2 改进的半解析有限元方法

在有限元方法计算中，大部分研究学者应用的钢轨弹性模量值为C=210 GPa，还有一小部分研究学者应用的弹性模量值为C=200 GPa。实际上，钢轨的弹性模量并不是一成不变的，它与环境温度相关。钢铁研究总院应用动态弹性模量测试仪测定了不同环境温度下CHN60型钢轨的弹性模量，结果表明二者呈反比例关系[15]。弹性模量的变化会改变导波的传播速度，从而造成较大的缺陷定位误差。因此，考虑引入环境温度T，改进半解析有限元算法。将弹性模量C用含有环境温度T的代数式表达：

C=C(T) , (6)

则钢轨中导波传播的动力学方程由式(5)改为式(7)的形式。

[K1(T)+iξK2(T)+ξ2K3(T)-

ω2M]MU=0 . (7)

分别计算环境温度为-20 ℃和40 ℃时对应的3号轨腰扭转模态的群速度频散曲线，如图4所示。

由图4可知，频率为30 kHz时，-20 ℃与40 ℃两种状态下，弹性模量相差3 GPa，群速度差值高达15 m/s。对于分别应用210 GPa和200 GPa的弹性模量进行计算的研究而言，二者群速度的差值甚至高达50 m/s。而随着频率增大，二者差值将继续增大。在实际应用中，将造成较大的定位误差。因此，计算群速度时引入环境温度变量对提高定位准确度非常重要。

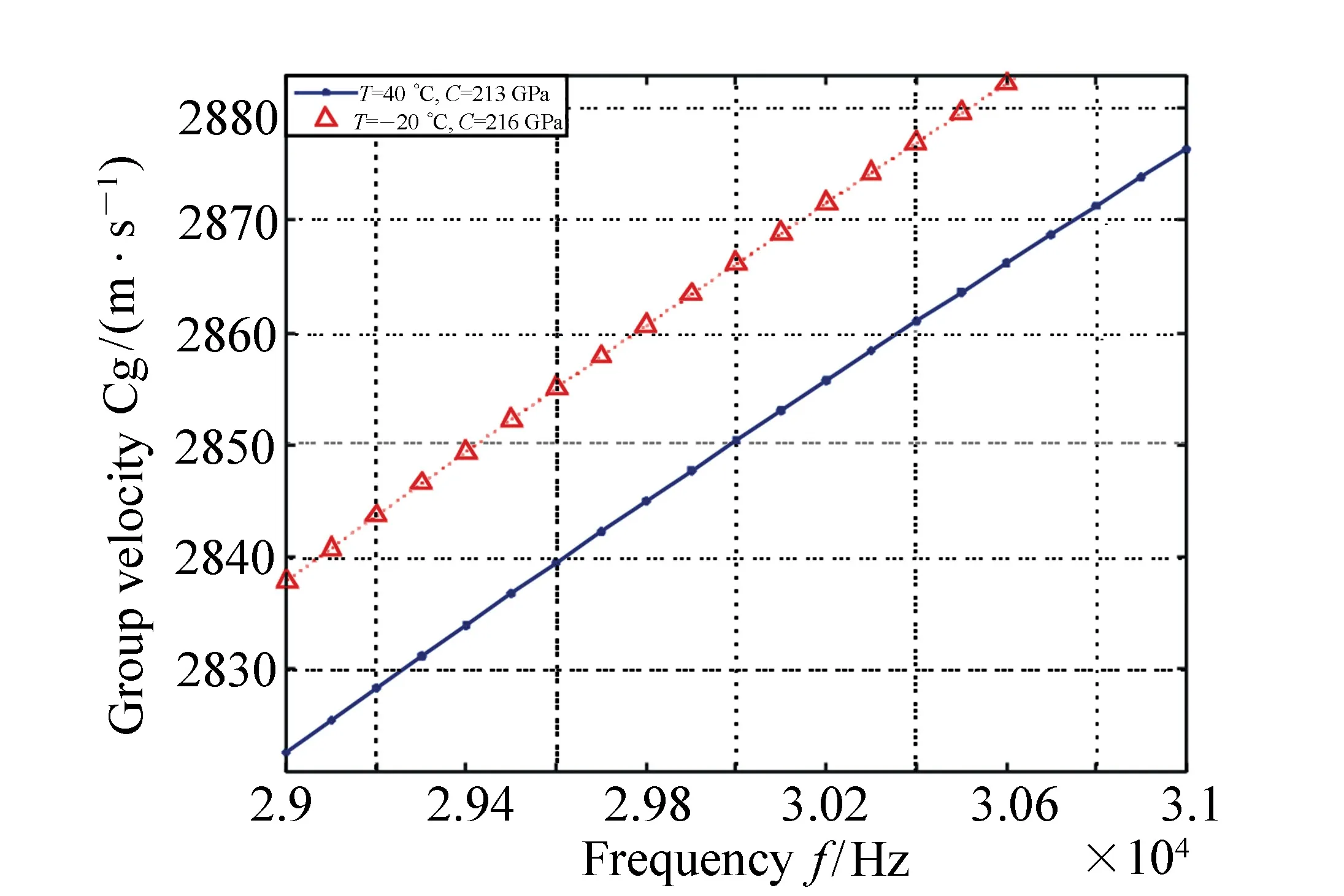
图4 -20 ℃和40 ℃时3号轨腰扭转模态频散曲线 Fig.4 Dispersion curves of rail waist torsional mode for No.3 rail at -20 ℃ and 40 ℃

3 频率选取

在同一频率下，钢轨中可激励出多个导波模态，不同的激励位置激励出的主要模态也不相同。各个模态的传播速度、振动特性、传播距离及其对缺陷的敏感度也不同。因此，应选择合适的频率和激励方式来激励出适于检测相应缺陷的模态。

3.1 频率选择

不同频率导波信号的传播距离与频率的关系如图5所示[16]。由图5可知，频率在40～60 kHz范围内的超声导波传播距离最远；频率在20～40 kHz的导波传播距离与40～60 kHz的信号相差不大，均较0～20 kHz的信号传播距离远很多。

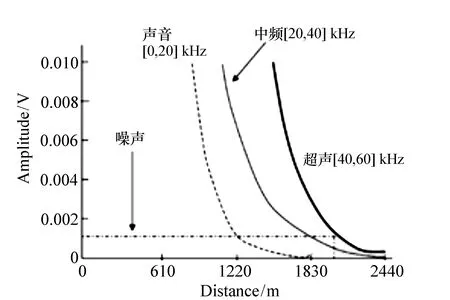
图5 钢轨中声波的衰减曲线图 Fig.5 Attenuation curves of sound waves in rails

由图3可知，在20 kHz时有14个导波模态，40 kHz时有23个导波模态，60 kHz时有33个导波模态。导波模态数量的增多使钢轨内信号的传播变得十分复杂，因此应在满足远距离传播的基础上，尽量选择频率较低的导波信号进行钢轨内的缺陷检测。然而，换能器在设计时遵循频率和直径成反比的规律，当频率选择过低时，换能器的直径将过大，安装在线路上会影响列车的安全运营。综合考虑上述因素，最终选取频率为30 kHz作为导波信号的激励频率。

3.2 振型分析

钢轨在频率为30 kHz时共有18种模态，模态振型图如图6所示。

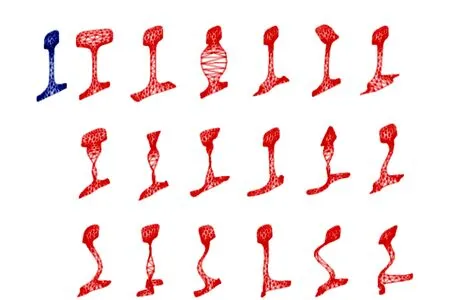
图6 钢轨中各模态的振型 Fig.6 Vibration shapes of various modes in rails

从振型图中可以看出，不同模态的振型形态各不相同，主要产生振动的部位也有所差异。如图6中，频率为30 kHz时，1号模态主要振动部位是轨头，3号模态主要为轨腰振动，而4号模态则是轨底振动。根据铁路现场情况，无缝线路钢轨的轨底均被扣件约束，对于轨底振动较大的振型，在振动时受扣件的阻碍无法远距离传播，因此在缺陷检测中应尽量避免选取此类模态。同时，为了不影响列车的正常运营，实现缺陷的在线监测，换能器应安装于轨腰位置。综上，根据图6选取了主要振动为轨腰振动的3号模态进行缺陷检测，振型如图7所示。

图7 模态3的振型 Fig.7 Vibration shapes of mode 3

当环境温度为32 ℃时，该模态的相速度值为2 184.8 m/s，群速度值为2 853.6 m/s。振动形态如图7所示，其轨头和轨底几乎不产生振动，轨腰处呈扭转振动形态，振动幅度很大。

4 激励响应计算

不同的激励位置及激励方式可以激励出不同的模态，因此在选定检测缺陷的模态后需要对该模态的激励位置及激励方式进行研究。应用激励响应算法计算出激励信号的传播情况，可以判断信号中是否激励出选取的模态。

在求解钢轨中任意信号的激励响应结果时，首先，应得到钢轨近似的系统函数模型H(jω)；然后将激励信号作傅里叶变换，得到频域信号V1(jω)。激励响应结果由V2(jω)=H(jω)·V1(jω)计算得出；最终对计算结果进行反傅里叶变换，即可得到时域结果。通过对时域结果的波形进行数据处理及分析，可得到波形中模态的群速度，与频散曲线及振型图进行对比，即可对信号中存在的模态进行判断。

建立钢轨模型函数表达式[17]：

(8)

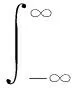
将激励信号v1(t)转换为频域[18]：

根据激励响应算法可计算出响应结果的频域表达式[11]：

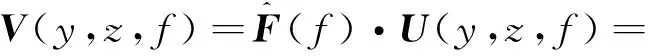
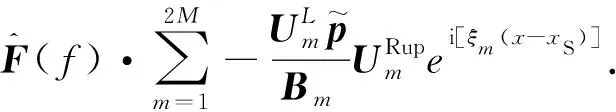
将式(10)的计算结果转换回时域，即为激励信号的响应结果。

现阶段还没有可以激励出指定的较为纯净的单一模态的方法，通常意义上的单一模态是指信号中该模态比例较其他模态多很多。一般需要布置阵列传感器，通过设置阵列中不同晶片的激励方式来激励出特定模态。考虑到线路上安装的方便性，希望可以只应用一个超声导波换能器即可达到阵列的激励效果，因此计算激励响应来验证方法的可行性。

由图7所示振型图可以看出，该模态的最大振动点在轨腰位置，考虑到采用30 kHz换能器的振动方向是纵向振动，因此将激励信号选为施加在轨腰中心，沿着钢轨截面的横向激励，如图8所示。激励信号的频谱如图9所示。

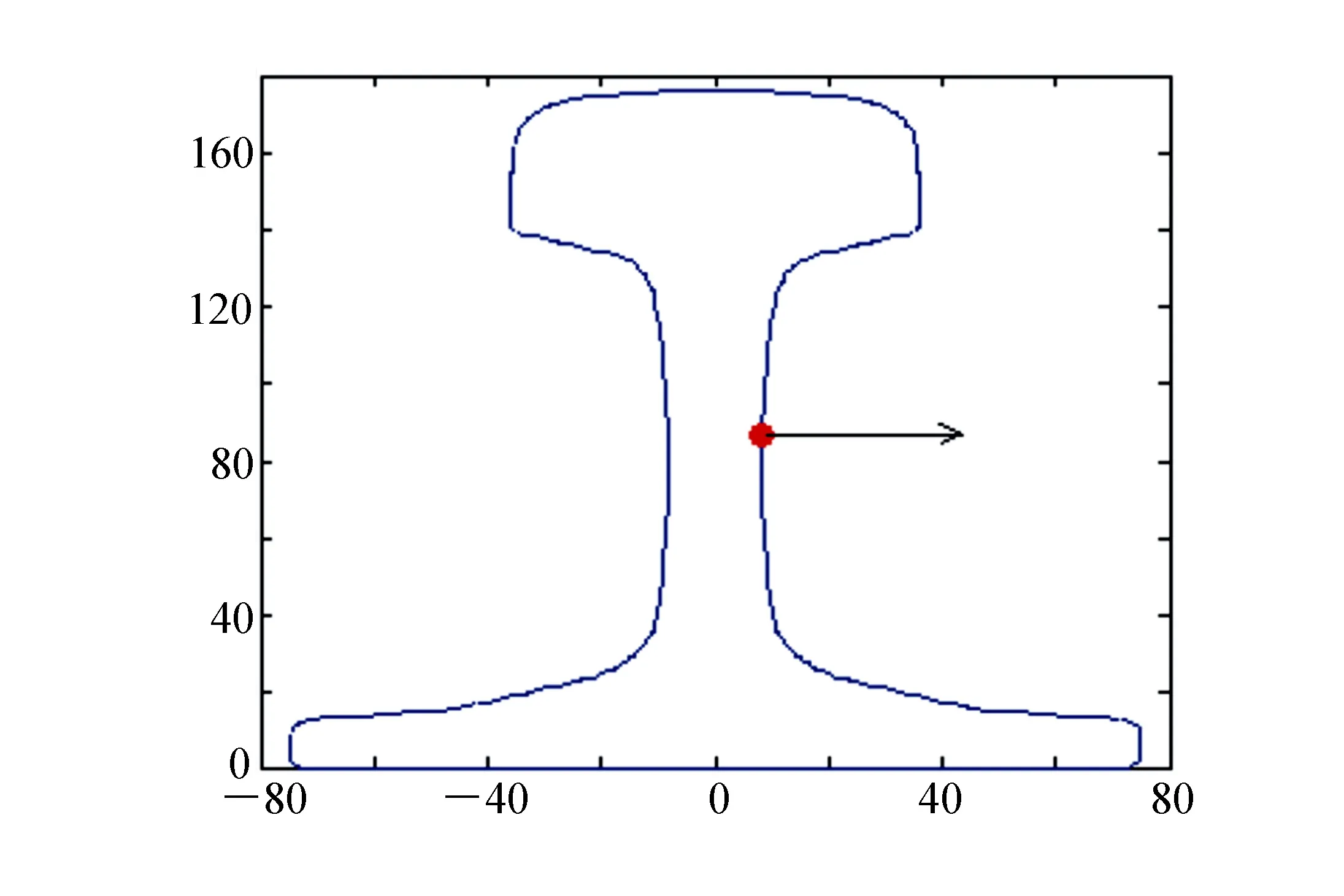
图8 激励方向和位置 Fig.8 Excitation direction and position

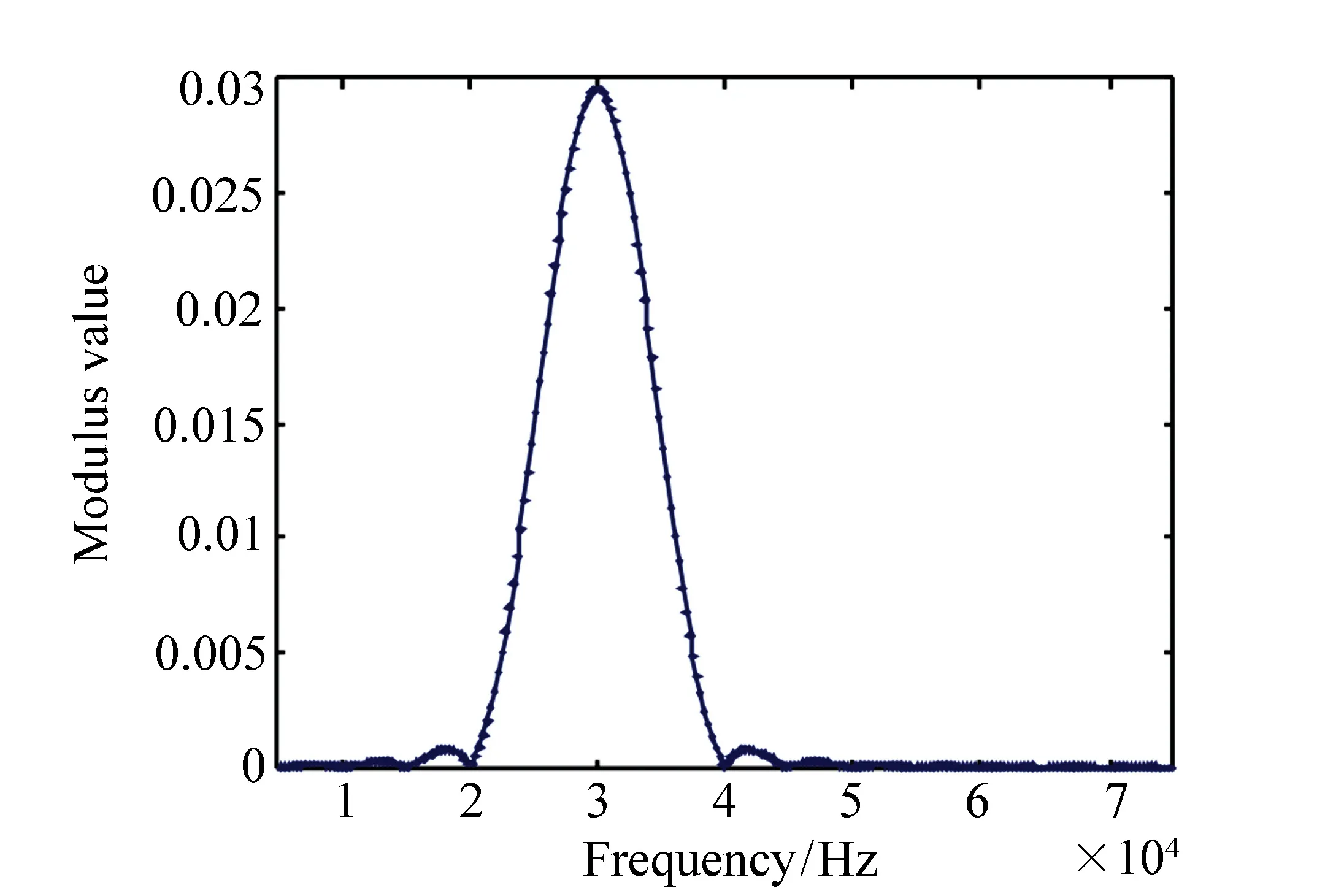
图9 激励信号频谱 Fig.9 Frequency spectrum of exciting signal

选择15～45 kHz间频率值进行激励响应计算，共计110个计算点。y方向激励轨腰中心节点，根据公式(10)求解出距离激励点4 m处的响应结果，并转换回时域，如图10所示。图中为4 m处轨腰中心节点y方向的位移，根据群速度定义，激励信号包络峰值时间为0.116 7 ms，4 m外接收信号包络的峰值时间为1.522 ms，二者相差1.405 3 ms。由此求解出导波传播的群速度2 846.4 m/s，查找图3可知，群速度为2 853.6 m/s的3号模态与之最为接近。因此，可以通过在轨腰的中心安装换能器，沿着钢轨y方向激励得到3号模态。

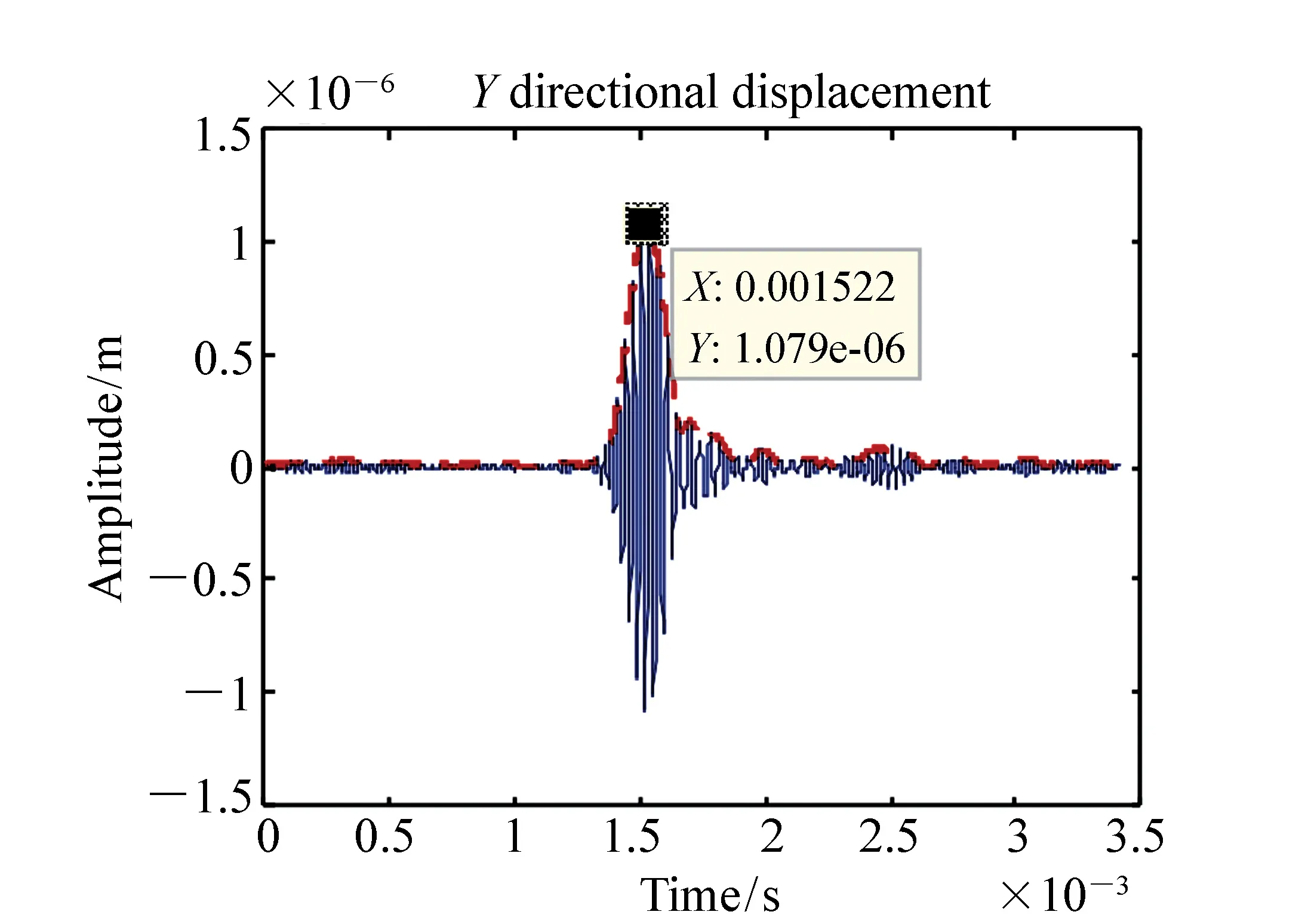
图10 4 m处轨腰中心y方向位移 Fig.10 Y direction displacement of rail waist center at x=4 m

5 现场实验

为进一步验证检测方法的可行性，在北京环形铁道试验基地进行了钢轨缺陷模拟检测实验。现场铺设钢轨为无缝线路长钢轨，在钢轨上分布了一些接地安装孔，如图11所示，以轨腰的接地孔作为模拟核伤，验证超声导波检测缺陷的可行性。

图11 轨腰接地孔模拟缺陷 Fig.11 Simulation defect of rail waist ground hole

5.1 模拟实验可行性分析

由于线路应用轨检车定期巡检，一旦发现缺陷立即换轨，很难找到缺陷。因此应用接地孔模拟钢轨上的特定缺陷，其作用是使导波在传播过程中产生脉冲回波，用以模拟缺陷的存在。所以接地孔可以作为产生反射回波缺陷的极限情况参与模拟实验。在众多缺陷类型中，钢轨核伤是情况最为严重的伤损类型，也是肉眼看不到的且对列车运行安全威胁性最高的伤损类型。因此，实验模拟的缺陷主要指钢轨的核伤。

为了验证模拟实验的可行性，分别建立了钢轨核伤三维模型以及接地孔三维模型，轨长均为20 m，核伤及孔均位于15 m处，网格大小为5 mm，核伤断面图及接地孔如图12所示。

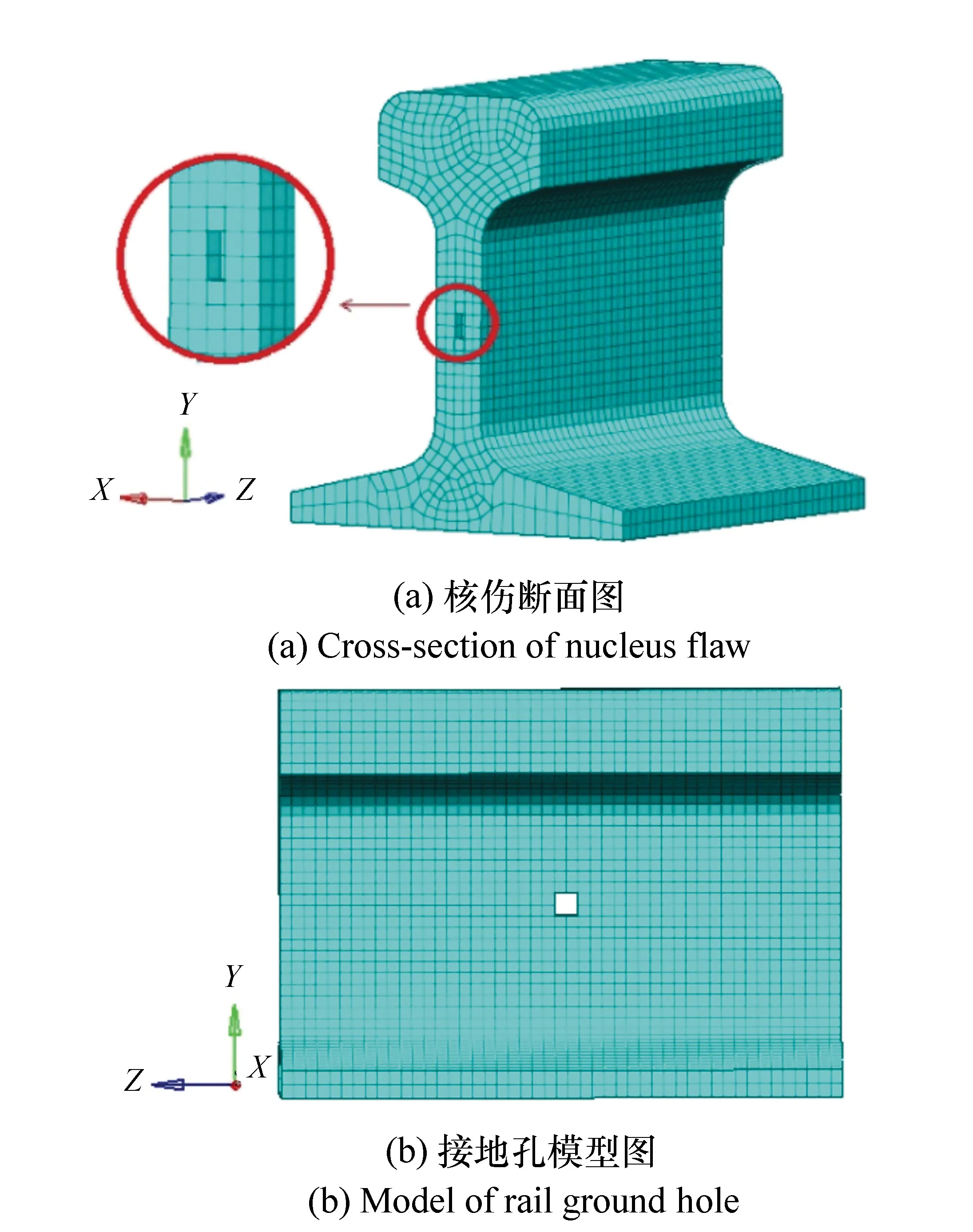
图12 仿真模型图 Fig.12 Simulation models

应用三维有限元仿真软件ANSYS分别仿真两条钢轨的激励响应情况。采用30 kHz信号横向激励钢轨10 m轨腰中心点，在13 m处接收振动信号，仿真时间为3 ms。这样设计可以保证缺陷反射信号已经传回，但端面反射信号还没有到达。提取两个仿真模型接收数据的反射回波信号，如图13所示。

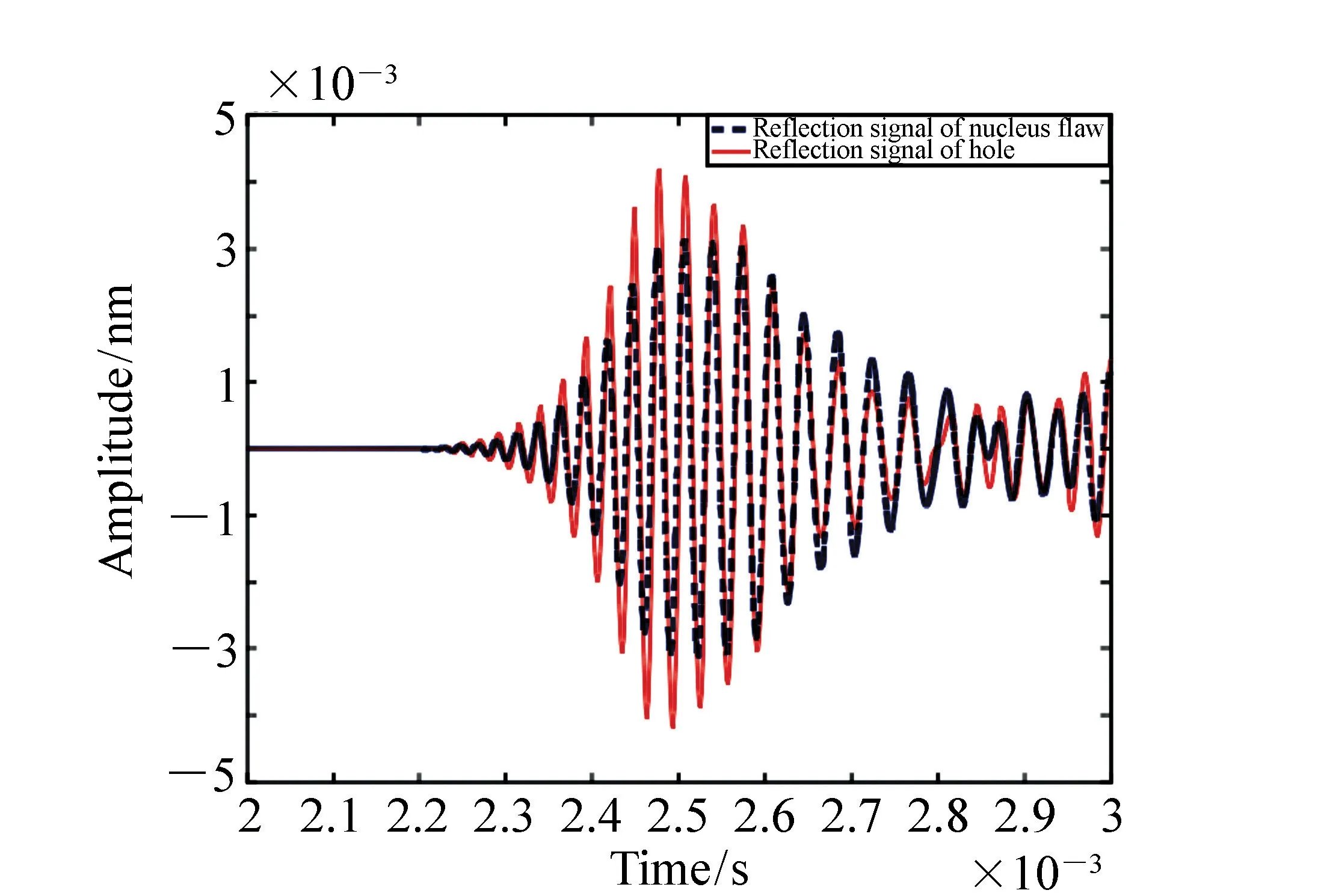
图13 回波信号 Fig.13 Reflection echo signal

由图13可知，二者反射回波波形一致，幅值略有差异。因此，钢轨核伤可以产生反射信号，且可以在缺陷检测实验中应用钢轨接地孔模拟核伤。

5.2 实验布置

导波发射探头通过磁性吸座固定在钢轨上，并采用耦合剂使接触面耦合，如图14。该传感器谐振频率为30 kHz，接触面为陶瓷，可以降低噪声的影响。

图14 发射换能器安装图 Fig.14 Transmitting transducer installation

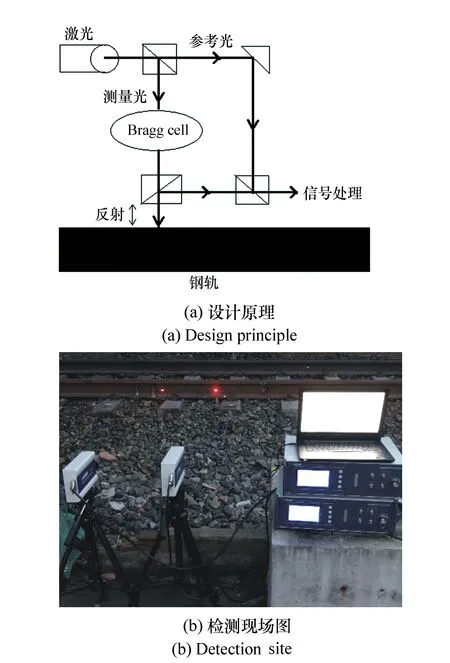
图15 设计原理及检测现场图 Fig.15 Design principle and detection image

为避免接触式检测方法受钢轨振动的扰动以及粘贴胶质等客观因素的影响，最大限度地减少仿真和实验的差异性，提高检测点的时空分辨率，降低接收器的非线性特性，实验采用基于光学差频干涉和激光多普勒频移的原理制作的激光测振仪搭配高精度解调卡来进行非接触式钢轨振动信号的接收。其设计原理及检测现场图如图15所示。用半反半透的玻璃镜将激光分为两束，分别作为检测光束和参考对比光束，检测光束经过Bragg cell进行频偏和钢轨表面的反射后与对比光束产生一个呈正弦变化的曲线，经过数据处理和标定得到实际振动速度。上位机自动采集速度信号后，将速度进行时间积分即可获得钢轨表面振动位移信号。当反射波的极值出现在一定区间时，产生报警并返回缺陷位置。

根据现场情况，在钢轨轨腰位置安装一个发射探头,并粘贴两张反光膜用于接收振动信号(两个接收点距离较近，第二个点用以辅助判断缺陷的方向及波包的传播方向)，探头和接收点前后各分布了1个接地孔，安装位置示意图如图16所示。

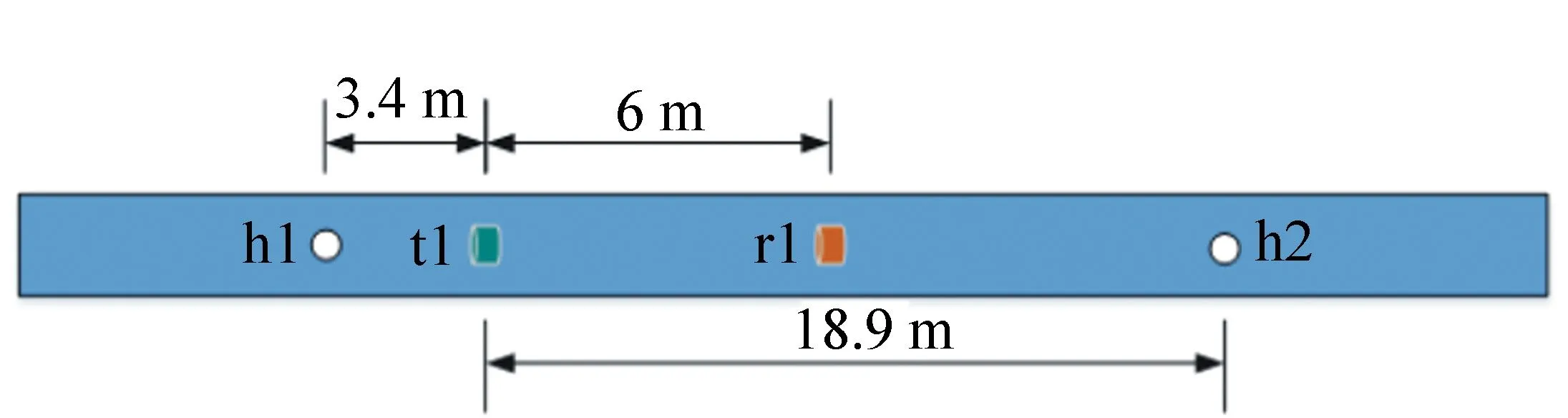
图16 换能器安装位置示意图 Fig.16 Sketch of transducer installation

图中激光头接收位置r1位于发射探头t1右侧6 m处，第一个接地孔h1位于发射探头t1左侧3.4 m处，第二个接地孔位于发射探头t1的右侧18.9 m处。

5.3 实验设置及结果分析

中心频率为30 kHz正弦信号激励钢轨，经汉宁窗调制后通过放大器输出施加在钢轨轨腰中心，发射间隔1 s。激光头接收的数据采集点数为100 000，上位机存储对每10次速度信号取平均值进行时间积分获得位移信号，设置报警下限为最大值的1/50，实验监测时长共6 h。以其中一组实验为例，r1的接收波形经过信号处理后如图17所示，其中实线为接收波形，幅值正半轴的最外侧虚线是包络线。

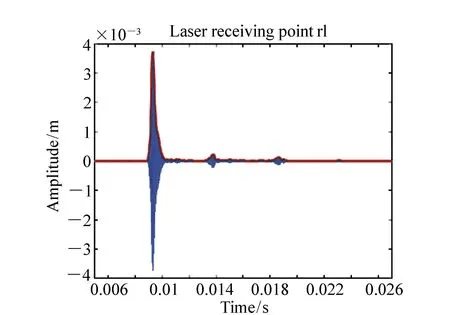
图17 接收点r1波形 Fig.17 Waveform of receiving node r1

由图17可知，第一个波包为r1点接收到的t1发射波，第二个波包是左侧孔h1的反射波，第三个波包是右侧孔h2的反射回波。实验时环境温度为32 ℃，激励出的3号模态的理论群速度为2 853.6 m/s。根据后两个波包与第一个波包的时间差和理论群速度可以计算出缺陷位置分别为发射点左侧3.35 m及发射点右侧19.33 m，与实际位置仅相差0.05 m和0.43 m。

分别移动激光头接收位置至发射探头右侧10 m和14 m处，再次重复实验，计算后得到的缺陷与t1距离及误差值见表1所示。

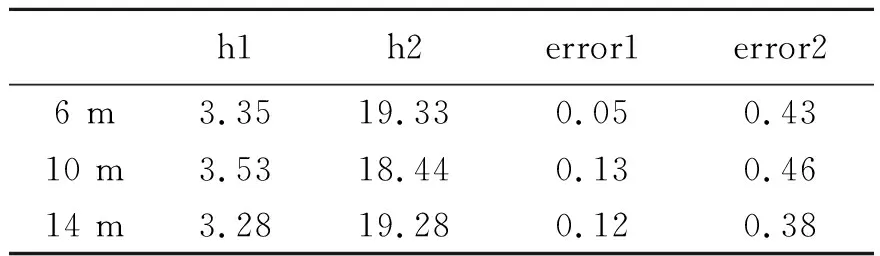
表1 缺陷位置估算及误差

经过现场实验验证发现，超声导波遇到缺陷后会产生反射回波，根据反射回波的接收时间及激励出模态的群速度可以实现缺陷位置检测。由于现场钢轨仅存在轨腰接地孔，现阶段无法实现轨头、轨底缺陷检测的模拟实验，待后期实验平台搭建完成后再进行相关实验。

6 结 论

针对现阶段我国铁路上应用的探伤设备只能在天窗时间进行巡检，无法在线监测的问题，提出了一种基于超声导波的钢轨内部缺陷检测方法。该方法应用改进的半解析有限元方法求解了我国CHN60钢轨的频散曲线，并选取了适用于检测钢轨内部缺陷的导波频率及模态，根据探头实际情况确定了激励方向，通过激励响应算法仿真了导波传播情况，从而确定了激励点。继而在北京环行铁道试验基地进行了现场实验，实验通过轨腰接地孔模拟了缺陷，应用激光多普勒频移法对钢轨单点振动信号进行非接触式采集，根据对采集信号的数字化处理，结合理论研究结果，实现了钢轨内部缺陷的检测。该方法的定位误差小于0.5 m。该方法激励方式简单，导波传播距离远，从接收方式上规避了产生接收换能器误差的可能，证实了应用超声导波全天候在线监测钢轨缺陷的可行性，提高了检测效率。同时，引入环境温度变量计算理论群速度，提高了定位准确度，为钢轨内部缺陷的检测提供了一个新思路。