广义回归神经网络在布鲁氏菌病预测中的应用

黄 璐,孙 娜，许小珊，田 野,马 洁，杜泽玉，孟维静，王素珍，石福艳

潍坊医学院公共卫生与管理学院 山东潍坊 261053

过去预测传染病时，往往将许多数学模型引入医学领域进行分析预测，如时间序列模型、灰色预测模型、多元线性回归模型等[1]。这些模型均为线性模型，但传染病的相关数据具有突发性且有受各种因素的影响不断变化的特点，通常是非线性的[2]，因此这类数据宜采用非线性模型预测。人工神经网络(artificial neural network，ANN)是数学模型的一种，具备模拟生物神经网络的功能，包含多个神经元，通过权值相连和非线性映射逼近处理非线性问题[3]。ANN在医学诊断、临床决策、预后和生存分析等领域中已得到了广泛的应用。广义回归神经网络(generalized regression neural network, GRNN)基于径向基神经元和线性神经元建立，是ANN的一种。GRNN最后将收敛于样本量集聚较多的优化回归面上[1]，在学习效率和函数逼近上优于径向基神经网络,同时容错性和鲁棒性很高[4]，训练过程中不需要迭代[5]，其网络训练参数只有一个，在参数保持一定的前提下，预测能力稳定；若不影响预测结果，则允许误差的存在。GRNN在解决数据较少的非线性问题时，也能保证预测效果。本研究基于我国布鲁氏菌病月发病人数，建立GRNN，预测布鲁氏菌病的发病情况，为布鲁氏菌病的防控提供科学依据。

1 资料与方法

1.1资料本研究数据资料来自国家疾病预防控制局(http://www.nhfpc.gov.cn/)发布的全国法定传染病疫情概况。研究收集了2010年1月到2017年12月的布鲁氏菌病月发病人数。

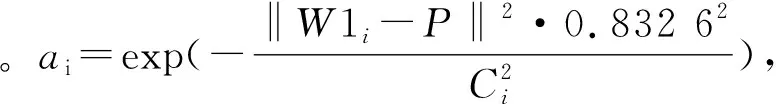
图1 GRNN模型结构图

模型建立过程中只有一个参数，即spread。通过交叉验证法来获取最优spread，使函数的逼近精确。随机抽取2010至2016年任意2个月的月发病人数作为测试集数据，将最小均方根误差(RMSE)[6]所对应的spread作为最优spread。

1.4模型检验采用平均相对误差及决定系数R2检验其预测和拟合效果[7]。R2=(SS实-SS误)/SS实，SS实为实际值的方差，SS误为误差(残差)的方差。

2 结果

2.1布鲁氏菌病的基本特征该数据为2010年1月到2017年1月布鲁氏菌病在全国的月发病人数。布鲁氏菌病为我国乙类法定传染病的一种，发病有明显的季节性，如图2所示，发病呈周期性递增趋势，集中在夏季。

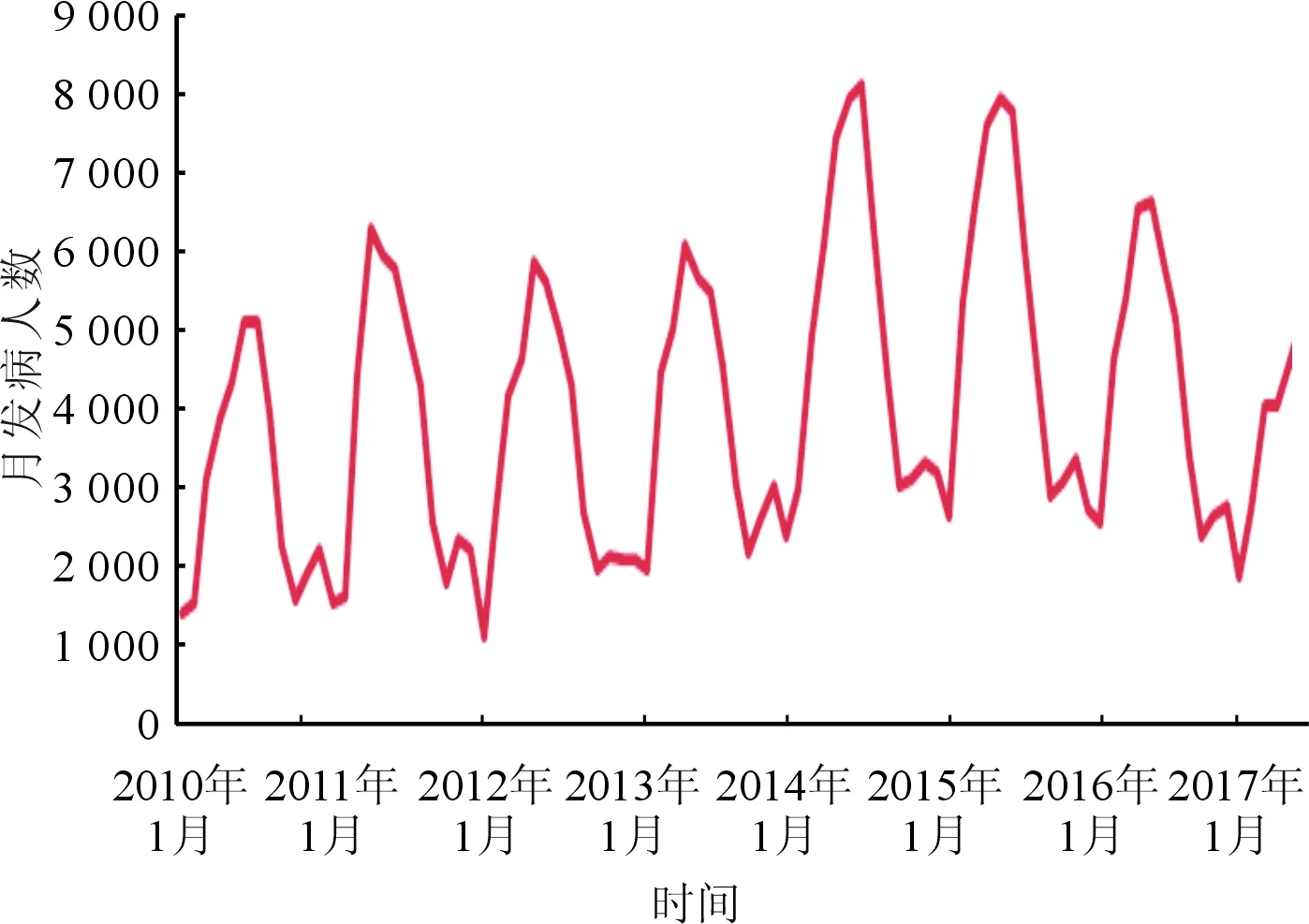
图2 2010年至2017年布鲁氏菌病月发病人数

2.2模型检验结果见图3。由图3知，当spread=0.02时，RMSE值最小，逼近误差小，逼近能力较强，此时模型的R2为0.64，拟合效果较好。

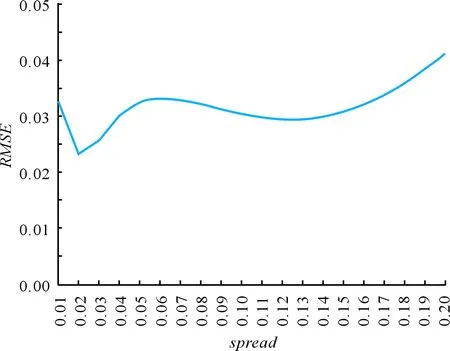
图3 不同spread对应的RMSE值

2.3布鲁氏菌病预测利用GRNN模型对2017年9至12月的数据进行预测，真实值和预测值的误差较小，平均相对误差为10.75%。结果见图4、表1。

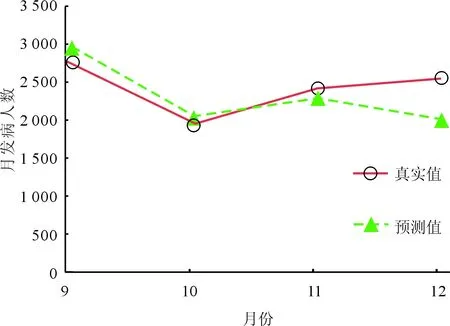
图4 2017年9至12月布鲁氏菌病月发病人数的预测图

月份真实值预测值误差相对误差/%92 7812 970-1897101 9532 045-925112 4272 2881396122 5492 00354627

3 讨论

布鲁氏菌病是我国乙类法定传染病之一，通过建立布鲁氏菌病疫情的预测模型，对该病的发生及发展趋势进行适当的预测，可为制定布鲁氏菌病的防控策略以及预防措施提供重要参考。

在对传染病的预测中，过去常借鉴数学模型，如自回归积分移动平均模型、灰色预测模型及马尔科夫链模型。不同的模型适用条件不同，各有利弊。线性模型预测(如灰色模型和时间序列模型等)对非线性的数据并不适用, 而非线性系统的数学模型又存在结构特定、辨识困难、处理复杂等问题[8]，实际应用困难。

ANN是模拟生物神经网络结构形成的非线性复杂网络系统。它能够逼近任意的非线性关系, 具有良好的泛化能力，能够学习和适应不确定的动态系统，从而更有效地解决医学中模糊、不确定的信息[9]。此外，ANN没有任何对变量的假设要求，不需考虑协变量间是否独立，因变量是否满足正态性。BP神经网络是目前应用最多的ANN，其工作原理运用已十分成熟，但也存在训练速度慢、局部最优等缺点[10]。GRNN径向基层通过高斯函数作为传递函数。高斯函数作为一种局部分布对中心径向对称衰减的非负非线性函数[11]，对输入信号在局部产生响应，即当输入信号靠近基函数的中央范围时，隐含层结点将产生较大的输出，所以这种网络具有局部逼近能力，学习速度也更快，解决了BP神经网络的问题，能够保证预测的效果。

GRNN是ANN的一种，作为一种数据处理方法，主要从数据上反映疾病的发展变化趋势[12]。本研究基于2010年1月到2017年8月的布鲁氏菌病月发病人数建模，预测2017年9至12月的数据。由于布鲁氏菌病的发病受畜牧、环境及个人防护等因素的影响，收集的资料数据是非线性的，而GRNN模型对资料的分布没有要求，结果显示，用25%的数据进行预测，真实值和预测值的误差较小，平均相对误差为10.75%，R2为0.64，模型的拟合效果较好，泛化能力较强，可为布鲁氏菌病的防控提供依据。另外，也可考虑将GRNN推广应用于其他传染病的预测，为传染病的防控提供科学依据。