基于有限元的行星减速器参数化动力学建模
迟 壮,王 伟
(中国民航大学a.乘务学院;b.航空工程学院,天津 300300)
行星减速器作为应用广泛的传动系统,以其高载荷、高可靠性和大传动比等优点应用于车辆、机器人等设备中[1]。但由于行星齿轮减速器结构复杂、装配紧凑,通过实验验证理论模型,需要测量的参量较多,且传感器不易安装,辨识过程也十分繁琐[2]。因此,基于技术上比较成熟的有限元分析方法,利用参数化建模完成传动系统的搭建,并通过对模型接触力的定义来模拟啮合过程,准确地模拟分析齿轮系统的接触、啮合等各种动力学行为,为理论模型的验证、优化提供依据。
1 行星齿轮减速器有限元建模
齿轮系统的动静力学仿真通常采用Pro/E、UG等三维机械建模软件,再通过中间格式导入有限元前处理软件完成[3]。这种方式对于建立单一齿轮系统模型简单高效,但在需要对不同参数的齿轮进行分析的设计优化中,则需要反复重复这一过程,效率会显著降低,且通用图形格式导入的模型会有细节上的失真,影响分析的准确性[4]。采用APDL参数化语言建立行星齿轮系统的有限元模型,可很好地克服上述缺点,建模结果准确,且可方便地完成参数化过程,以便对不同的齿轮模型进行分析。
1.1 参数化前处理建模
机械关节中使用的行星齿轮结构较为复杂,一般采用同轴输入输出的2K-H型行星齿轮。要准确地描述其传动动力学行为,需建立所有部件的准确几何模型并设置合理的接触、耦合关系。齿轮系统的动力传递由轮齿的啮合来完成,因此,精确描述轮齿形状并合理划分网格是对齿轮系统准确建模的关键。
首先,设置单元和材料。选用的单元必须是LSDYNA显式动力学分析中允许的单元,为了消除沙漏带来的影响,齿轮和齿圈实体部分采用全积分SOLID164实体单元,设置MESH200平面单元辅助建模。在齿轮内孔表面覆盖SHELL163单元并定义为刚性材料,设置为0.1 mm的均匀厚度,选择S/R corotational Hughes-Liu单元以消除沙漏状态[5]。设置柔性材料用于实体单元划分,刚性材料用于内表面SHELL163单元和行星架的SOLID168单元,弹性模量、泊松比和密度等按照实际材料属性设定。另外,还需要定义MASS166单元用于模拟输出端负载惯量。
其次,根据齿轮的几何参数建立半齿面的参数化模型,如图1所示。按照渐开线生成原理齿廓曲线,以齿轮中心为坐标原点建立圆柱坐标系,在齿廓曲线上按照半径间隔取n个极坐标点,其坐标值[6]可表示为

其中:ra为齿顶圆半径;rb为基圆半径;z为太阳轮齿数;θi为齿廓点对应的展角;j为法向齿侧间隙;r为齿轮分度圆半径。

图1 半齿面的参数化建模Fig.1 Parametric modeling of half tooth surface
图1 中L5为渐开线曲线,按式(1)选取若干点,使用BSPLINE命令沿所求得的点绘制即可得到:以齿轮中心为圆心的圆弧L1、L2、L6;齿根过渡圆弧L7,其半径为0.38 m(m为齿轮模数);直线L3、L4。计算的关键在于渐开线齿廓上的接触载荷,可根据计算精度利用ANSYS的LESIZE命令对渐开线L5进行网格细分控制。
完成半齿面后,以L3为基准进行镜像操作及布尔加和运算,即可得到一组全齿面建模。以原点坐标为中心,将全齿面转动到拟分析啮合位置,再将平面全齿面旋转复制z次,即可得到太阳轮的平面网格。随后使用VOFFSET命令,基于SOLID164单元进行轴向拉伸,即可得到完整的网格化的太阳轮三维建模。拉伸前,应使用EXTOPT命令控制拉伸段数,拉伸段越多计算结果越精确,但会造成实体单元数的迅速增大,影响计算效率[7]。啮合刚度主要取决于啮合平面内的单元数,轴向精度对其影响不大,在单元性质允许的范围内可选择尽可能小的拉伸段数以减少单元数量。图2为拉伸2段后形成的SOLID164单元太阳轮有限元模型。

图2 轴向拉伸2段的太阳轮模型Fig.2 Sun wheel model after two sections of axial tension
按照同样的方法在行星轮、内齿圈局部坐标系内完成相应建模,多个行星轮可采用VGEN命令在太阳轮中心坐标系内沿周向复制完成。在复制行星轮的过程中使用*DO循环语句,且将行星轮个数np设置为可变参量,即可满足不同行星轮个数的要求[8]。需注意,内齿圈与行星轮之间的啮合方式为内啮合,建立齿面时应选择与外啮合轮廓相反的方向。
相比齿轮的啮合部分,行星架并不会产生较大变形,所以划分网格时可选用刚性材料的SOLID168单元,单元也可以尽可能划分的稀疏。最后,再在行星架输出端轴轴心处设置一个节点用以连接MASS166惯性单元,以模拟负载特性。为了实现网格的精确控制,需要用NUMMRG命令对相邻相近节点进行重复压缩,使建模后的面、体和单元等在结构上处于各自独立的状态,从而得到了如图3所示的完整的行星齿轮三维实体有限元模型。

图3 完整的行星齿轮有限元模型Fig.3 Complete finite element model of planetary gear
图4 为采用此方法建立的不同行星轮数、齿数、模数、齿宽的行星齿轮系统模型,参数化建模的优势在此体现出来。

图4 参数化程序建立的不同行星齿轮模型Fig.4 Different planetary gear models established by parametric program
1.2 接触、载荷和边界条件设置
LS-DYNA建模中存在PART概念,采用不同单元、材料和实常数定义实体,再通过EDPART命令自动生成PART。不同PART间可设置接触,并为加载和数据后处理提供方便[9]。在设置时,注意相同单元和材料的实体可采用不同实常数号加以区分。
一般来说,行星齿轮系统作为减速器使用时,需固定行星轮外齿圈,太阳轮一端作为输入,行星架一端作为输出。因此,在设置约束时,首先要选定外齿圈外圆柱面上所有节点,并约束所有转动、平动自由度。
LS-DYNA可使用ARRAY数组进行加载,首先需要设定时间数组,再设定相应的转角、角速度或角加速度数组,转矩也采用相同的方式[10]。在加载转矩时,还需建立局部坐标系,并在该局部坐标系内使用EDLOAD命令加载设定好的转矩数组。
加载程序如下:

行星轮与行星架一般采用轴承连接,可采用转动副约束完成,需要修改LS-DYNA关键字文件。
在关键字文件内添加的关键字如下:


在导出关键字文件前,还要在行星轮、行星架连接转动副关节位置设置两个同轴的节点,这样即可分别在行星轮和行星架预留的节点上定义转动副,传动关系通过3对理想转动副传递,极大减少计算量。
2 仿真结果
设置计算时间控制、输出文件控制和高级求解控制后,利用LS-DYNA显式求解器进行求解,可得到行星齿轮在高速转动过程中的啮合接触和冲击情况。
图5为无侧隙行星齿轮减速器运行过程Von Mises应力云图。在无侧隙情况下,啮合基本呈现出连续接触状态,由接触变形导致的反向啮合时而发生,但并不明显,齿轮组运行比较流畅。从应力云图分布来看,啮合应力的最大值出现在轮齿的接触位置,最大应力值为0.3~0.4 GPa。相比之下,轮毂部分的应力较小。图5(a)为齿轮开始产生啮合时的应力分布情况,3个行星轮6对啮合同时产生,但每对啮合参与的齿数不同,证明了考虑啮合相位的必要性。图5(b)中,左下角行星轮的啮合力明显高于另外两个行星轮,这说明行星齿轮在运转过程中存在不均载的问题。
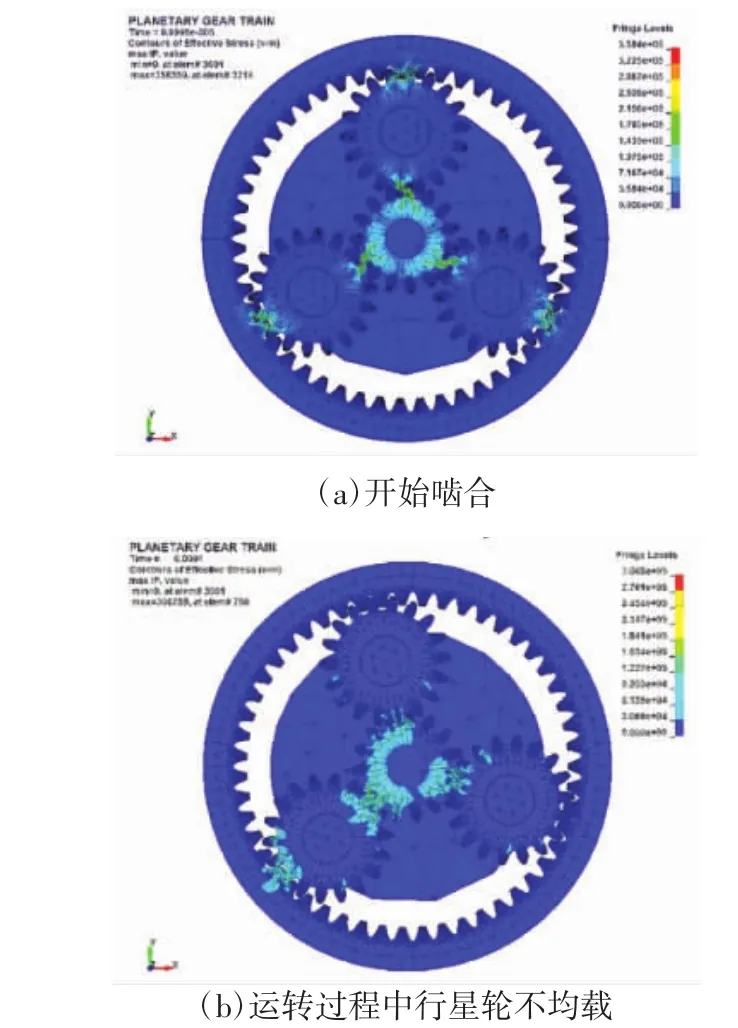
图5 无侧隙行星齿轮减速器运行的Von Mises应力云图Fig.5 Von Mises stress nephogram of planetary gear reducer without side clearance during operation
图6 为侧隙500 μm的行星齿轮减速器运行过程Von Mises应力云图动态变化截图。与无侧隙情况相同的是最大应力分布仍处于轮齿的啮合区。不同的是,有侧隙时会出现比较明显的反向冲击和空转的情况,如图6(b)所示,这时齿轮内部应力明显减小,太阳轮空转时,内部最大应力仅为0.1 GPa左右。图6(c)内不均载时刻的应力分布,最大应力达到0.6 GPa左右。太阳轮内产生高频率的周期性应力变化,势必导致太阳轮在运转过程中产生疲劳甚至失效的可能。

图6 有侧隙行星齿轮减速器运行过程VonMises应力云图Fig.6 Von Mises stress nephogram of planetary gear reducer with side clearance during operation
图7 和图 8分别为内外啮合齿轮在一个完整啮合周期内的应力分布情况图。从图中可清楚地看出内外啮合过程都分别经历了单齿啮合—空转—双齿啮合的转换过程,且在齿侧间隙存在的情况下,会产生比较明显的反向啮合冲击。
另外,为了体现参数化建模分析的优势,图9为采用参数化程序建立的不同侧隙大小的输出转角曲线。从图9中看出,侧隙的增大对于减速器的输出转角精度影响不大。而图10中的角速度曲线在侧隙增大时则出现明显的不同。在转动初期,轮齿持续出现啮合碰撞,而较大的齿侧间隙在碰撞回弹过程中会产生空程。

图7 太阳轮-行星轮外啮合过程Fig.7 External meshing process between sun wheel and planetary gear

图8 内齿圈-行星轮内啮合过程Fig.8 Internal meshing process between inner annular gear and planetary gear

图9 不同侧隙下的转动角度Fig.9 Rotation angles under different side clearances

图10 不同侧隙下的转动角速度Fig.10 Rotation angular speed under different side clearances
3 结语
借助APDL语言编写了行星齿轮减速器自下向上的参数化建模方法,建模过程无须借助三维建模软件,可快速有效地完成不同参数的行星齿轮有限元模型建模。利用该程序完成了一组2K-H行星齿轮减速器的前处理建模,并通过修改关键字文件完成了约束、加载和接触的设置。最后采用LS-DYNA显式积分求解器求解,模拟出行星齿轮运转动态过程,分析了啮合过程中存在的冲击、不均载等现象。研究不同齿侧间隙的有限元模型动力学响应,为行星齿轮减速器的运动学分析提供有效方法。研究结果表明:①行星齿轮在运转过程中,应力主要集中在轮齿的接触部分,且行星轮间会出现不均载现象;②当存在较大的齿侧间隙时,太阳轮内会出现比较显著的周期性应力变化,侧隙同时还会带来脱啮、反向冲击等现象;③对关节进行往复运动的精确控制时,必须将由齿侧间隙产生的角速度误差累积导致的输出角度精确性变化考虑在内。

