基于GSO-BP神经网络的磷酸铁锂电池SOC预测

王丙元，张丹丹

（中国民航大学电子信息与自动化学院，天津 300300）

电动汽车产业是中国产业发展的一个战略重点。电池是电动汽车的动力源，磷酸铁锂（LiFePO4）电池已成为电动汽车电池的首选。车辆续驶里程和行驶性能主要取决于动力电池组的荷电状态（SOC）[1]。如何有效提高SOC预测精准度对提高电动汽车续航能力以及电动汽车发展具有现实意义[2]。

传统的磷酸铁锂电池SOC预测方法大都是在电池内部物理化学反应基础上建立数学模型[3-4]。过多的假设条件和经验参数，导致计算复杂且预测精度低。而采用传统的优化神经网络在预测磷酸铁锂电池的SOC时存在易陷入局部最优且训练时间较长等缺点[5-7]。研究提出的萤火虫优化算法（GSO）可实现全局最优[8]。相比其他算法，萤火虫优化算法无需目标函数的梯度信息，具有鲁棒性、易实现和易用性等优点。

1 基于BP神经网络的SOC预测模型

BP神经网络无需建立数学模型即可用于复杂系统的预测与控制[9]。一个三层神经网络可以逼近任意精度的连续函数，故采用三层BP神经网络来预测LiFePO4电池的SOC。研究表明，放电电压和放电倍率是影响SOC状态的主要因素[10-11]，将放电电压和放电倍率作为BP神经网络输入，SOC作为网络输出。在GSO-BP神经网络的输入层设置2个节点，输出层设置1个节点，通过多次仿真实验将隐含层节点数设置为5，因此共15个权值和6个阈值。三层BP神经网络的网络结构如图1所示。

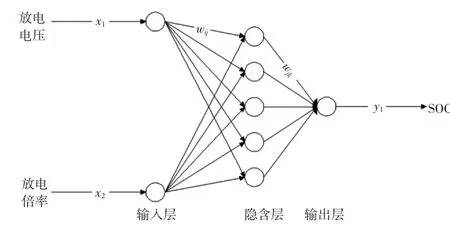
图1 基于BP神经网络的SOC预测模型Fig.1 SOC prediction model based on BP neural network

2 萤火虫算法

萤火虫算法的核心是利用萤火虫发光特性向邻近空间内亮度高于自己的萤火虫位置移动，通过位置更新而实现优化[12]。GSO算法主要分为以下4个步骤：初始化萤火虫、荧光素更新、位置更新和决策域更新。

设萤火虫的种群规模为N，其中第i只萤火虫所在位置为xi（t），该位置对应一个适应度函数为f（xi（t）），其荧光素值为li（t），每只萤火虫的决策半径更新公式为

在萤火虫i的决策域范围内萤火虫数量由式（2）决定，即

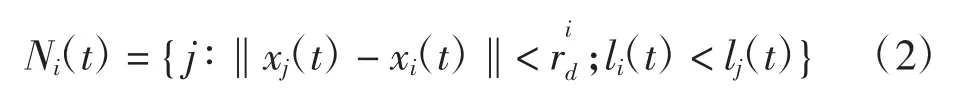
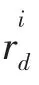
在GSO执行过程中，萤火虫i的运动方向由其所有邻居中各萤火虫的荧光素数量来决定，在第t次迭代中萤火虫i向其邻居萤火虫j移动的概率Pij（t）为

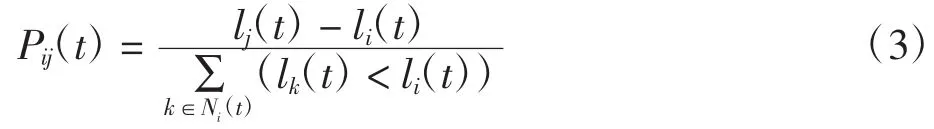
萤火虫位置更新公式为

其中，s为移动步长。

萤火虫的荧光素值更新公式为

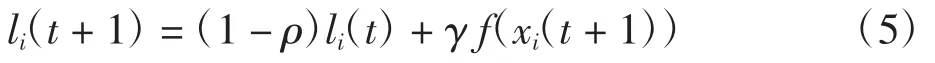
其中：li（t）为萤火虫i在第t次迭代中的萤光素值；ρ∈（0，1）为常量，表示荧光素挥发因子；γ为荧光素更新率。

在邻居集合中，当萤火虫i寻找到荧光素值更高的萤火虫j时，且若此时萤火虫i和萤火虫j的距离小于感知半径，则萤火虫i会以概率Pij（t）向萤火虫j方向移动；然后按照式（4）更新位置，并且计算新位置的目标函数值；最后，根据式（5）更新萤光素值。

3 GSO-BP磷酸铁锂电池SOC预测

3.1 网络构建与数据选取

磷酸铁锂电池SOC预测需考虑的因素有很多，在进行磷酸铁锂电池SOC预测时必须综合考虑，研究选取电池的放电电压、放电倍率作为预测指标，在三层BP神经网络中，选取这2个典型指标作为网络输入，荷电状态SOC为网络输出，以生成GSO-BP神经网络的磷酸铁锂电池SOC预测模型。

3.2 预测模型建立

萤火虫算法优化BP神经网络的基本思想是：确定BP神经网络的结构，然后通过萤火虫算法优化BP神经网络的初始权值和阈值，最后完成优化后的神经网络预测。下面对模型进行具体分析。

1）数据预处理

原始数据预处理包括数据量化和归一化。预处理后的数据能够被GSO-BP神经网络读入。

2）训练集/测试集产生

为保证训练数据随机性，随机选取测试数据库中48组数据作为训练集，其余200组数据作为测试集。

3）GSO-BP 神经网络

把训练集输入构建好的GSO-BP神经网络，然后进行网络训练，具体步骤如下：①利用GSO算法对BP神经网络的初始权值和阈值进行优化，再利用优化后的最优权值和阈值构造BP神经网络；②GSO-BP网络创建完毕后，便可将训练集向量输入到网络中，利用GSO-BP神经网络对网络的权值和阈值进行优化调整，直至满足训练要求，迭代终止。

4）磷酸铁锂电池SOC测试

网络训练完成后，即可对测试集的磷酸铁锂电池SOC进行预测。

3.3 预测算法

GSO算法具体实现步骤如图2所示。

图2 基于GSO-BP神经网络的预测算法框图Fig.2 Prediction algorithm based on GSO-BP neural network

1）种群初始化

个体编码方法为实数编码，每个个体均为一个实数串，每个实数串都包括输入层与隐含层的权值、隐含层的阈值、隐含层与输出层的权值以及输出层的阈值。每只萤火虫都包含了整个神经网络所有的权值和阈值，当网络结构确定的状况下，就能够构成一个结构、权值和阈值明确的神经网络。

2）适应度函数

通过最优个体的编码能够得到BP神经网络的最优权值和最优阈值，用训练数据训练BP神经网络后得到预测输出，将预测输出和期望输出之间的误差绝对值的和作为适应度函数，计算公式为

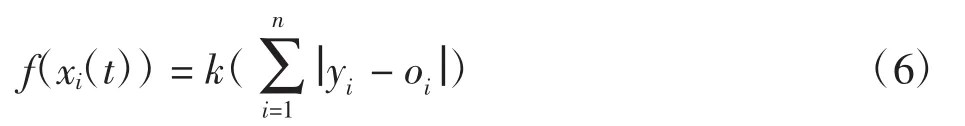
其中：n为网络输出节点数；yi为BP神经网络第i个节点的期望输出；oi为第i个节点的预测输出；k为系数。

3）荧光素更新操作

对种群中的每一只萤火虫i按式（6）计算在第t+1次迭代中的位置xi（t+1）的适应度值，然后按照式（5）通过适应度函数值求得萤火虫i的荧光素值。

4）位置更新操作

在萤火虫算法中，如果萤火虫i寻找到荧光素值更好的萤火虫j时，两只萤火虫的距离则小于决策半径，萤火虫i以概率Pij（t）向萤火虫j方向移动；然后根据式（4）更新位置，并根据式（6）计算新位置的适应度函数值，从而更新全局最优值。

5）决策域更新操作

在位置更新后，萤火虫i会根据其邻居密度按照式（1）动态更新决策半径。倘若邻居密度太小，决策半径就会增大，从而更有利于寻找更多的相邻萤火虫；反之，则减少半径。

4 模型仿真与验证

4.1 电池数据库的建立

试验选用磷酸铁锂电池的额定电压为3.3 V，容量为1 100 mAh。使用ITECH系列的直流电子负载和直流电压源等设备进行充放电实验，同时对4组磷酸铁锂电池进行性能实验，记录电池放电电压、放电电流、充放电倍率这几种参数的变化过程，每隔1 s采样一次实验数据，测试周期为1个月。

1）训练与测试样本数据选取

当室温为25℃时，分别按照0.5 C、1.0 C、2.0 C和5.0 C的放电倍率恒流放电测试，在每种放电倍率下选取12个典型的放电电压值作为输入，所测荷电状态值作为输出。从测试结果中选取248组数据作为样本，并将248组数据分为两部分，48组数据用来训练，200组数据用来测试，如表1所示。

表1 训练与测试样本数据Tab.1 Training and testing sample data

2）归一化处理

数据归一化是神经网络预测前对数据的预处理，是将网络中所有输入数据都转化为[0，1]之间的值。数据归一化的函数形式为

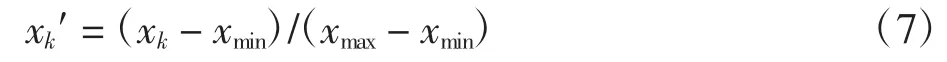
式中，xmin和xmax分别为数据序列中的最小值和最大值。

4.2 参数设置

在Matlab环境下，将归一化处理的数据用于该网络的训练和预测。参数设置如下：萤火虫算法个体编码长度为21，荧光素初始值l0=5，邻域变化率β=0.088，控制萤火虫邻居数目的邻居阈值nt=5，步长s=0.05，种群规模N=50，荧光素更新率γ=0.6，荧光素挥发因子ρ=0.4，萤火虫感知半径rs=6，迭代次数maxgen=100。进化参数设置为：学习率为0.01，训练目标为0.000 1。采用GSO-BP神经网络训练数据时，经过75次迭代后目标函数收敛于最佳适应度值0.37，找到满足该网络最小适应度值的权值和阈值。

4.3 仿真实验结果与分析

为了检验该优化后的网络性能，将表1的数据依次用GSO-BP、PSO-BP和GA-BP神经网络进行仿真，得到仿真结果如图3所示。

图3 锂电池SOC网络预测结果与实验测量结果Fig.3 SOC predicted and tested values of Li cell

图 3（a）、图 3（b）和图 3（c）分别是 GSO-BP、PSOBP和GA-BP神经网络的预测值和实际值对比图。通过分析图3可明显看出，仿真的GSO-BP神经网络的预测值比PSO-BP神经网络、GA-BP神经网络的预测值精度更高。

图4为荷电状态与放电电压的关系曲线。从图4中更能清晰地反映出经过网络结构优化后的GSO-BP神经网络具有较高的准确性和鲁棒性。

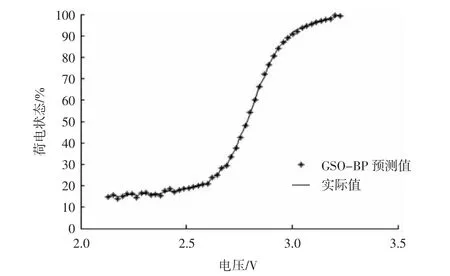
图4 放电电压与SOC关系曲线Fig.4 Relation curve between discharge voltage and SOC

图5 为Matlab仿真过程中的网络预测输出误差曲线图。由图5可知，当电压在2.1～3.25 V之间时，基于GSO-BP神经网络的磷酸铁锂电池SOC的预测误差小于1%，完全满足SOC预测误差5%的技术指标，而PSO-BP神经网络和GA-BP神经网络预测SOC误差最大时分别达到了9.2%和14.3%，可明显看出GSO-BP神经网络预测精准度最高。从仿真结果可得出如下结论，GSO-BP神经网络对SOC的预测结果比PSO-BP神经网络、GA-BP神经网络的预测结果更逼近实际值，其精准度更高。

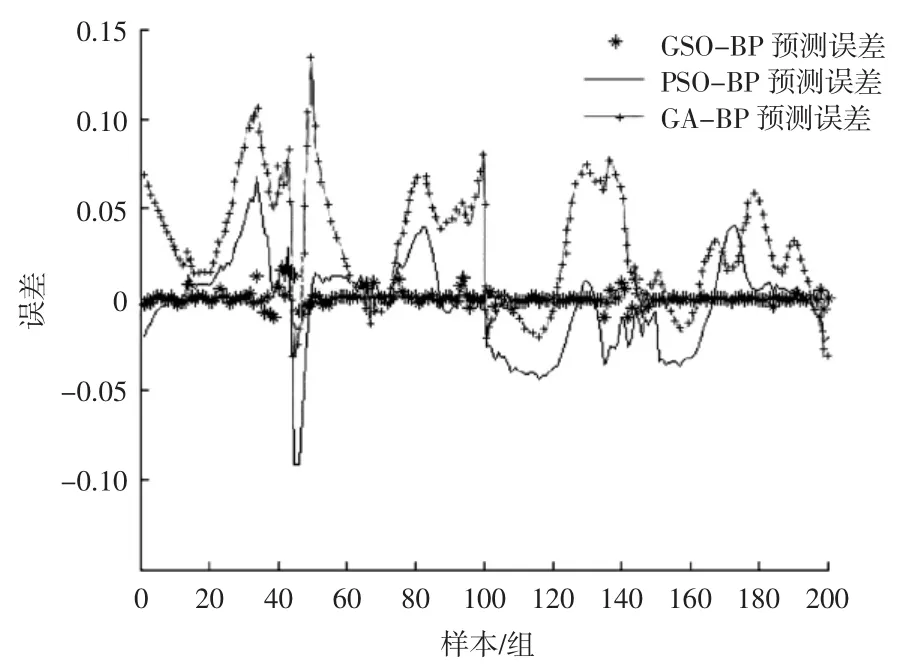
图5 网络输出误差Fig.5 Network output error

5 结语

建立了基于BP神经网络的磷酸铁锂荷电状态预测模型，利用萤火虫算法优化了BP神经网络权值和阈值，通过优化的BP神经网络结构预测磷酸铁锂电池SOC以提高预测精度。仿真结果表明，GSO-BP神经网络对SOC的预测结果比PSO-BP神经网络、GA-BP神经网络的预测结果更逼近实际值，其精准度更高。预测得到的磷酸铁锂电池SOC精度更能够满足蓄电池管理系统的要求。GSO-BP神经网络结构简单，有着很好的泛化性能，对其他工程应用具有一定的指导意义。