改进量子粒子群算法在航材初始配置中的应用

田 静，张恩豪，付维方

（中国民航大学航空工程学院，天津 300300）

当今国内外航空市场竞争日趋激烈，航空公司比以往任何时候都更加重视成本控制，而航材的初始购置成本是企业运营成本中的重要组成部分，因此对初始航材的成本控制是提高公司经济效益的重要途径。

对于航材初始配置的研究需要解决模型构建和求解两个问题。在模型构建方面，航空公司往往将保障率作为重要的保障目标，因此优化模型目标函数的构建中需以保障率为基础[1]，并引入成本变量，构建单位成本系统保障率最大的模型，将系统保障率均匀分配到每一单位成本上，寻求单位成本最大化，进而达到单位成本效益最高的目的。在模型求解方面，启发式算法[2]、遗传算法[3]、粒子群算法（PSO）[4]、量子粒子群算法（QPSO，quantumparticleswarmalgorithm）[5]等智能算法均被应用于函数优化问题的求解中。其中，粒子群算法因原理简单、操作性强被广泛应用，但粒子群算法存在无法以概率为1进行全局收敛的局限性[6]。为解决此问题，Sun等[7]和Wang等[8]提出具有量子行为的新型粒子群算法，即量子粒子群算法，该算法引入了吸引势的概念，通过建立量子化的势场对粒子进行约束，从而实现粒子种群的聚集性，扩大了粒子在空间的搜索范围，提高收敛能力。但标准的量子粒子群算法由于后期粒子多样性降低仍会存在过早收敛和全局寻优不完美的情况。针对此问题，需对进化因子和收缩扩张系数两方面进行改进，并将其应用于初始航材优化模型中。

1 模型建立

1.1 系统保障率模型

赵建忠等[1]提出改进系统保障率模型，该模型从系统保障率定义出发结合基层级维修方式，得出第i种备件的保障率Pi满足

其中：T为备件维修周期；Ni（T）是第i种备件维修周期（0，T）内需要进行更换的次数；Si（T）是第i种备件维修周期（0，T）内的库存量。而系统整体保障率可表示为

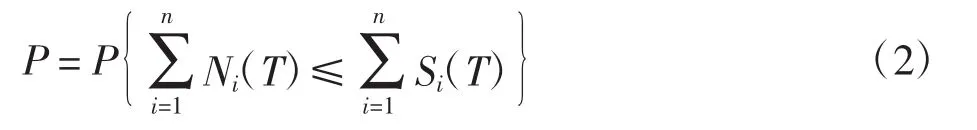
式中，n为备件种类数。

1.2 单位成本保障率最大模型

航空公司优化航材购置是为了实现效益最大化，即每单位成本内效益最大。因此在改进系统保障率基础上引入总成本变量，将单位成本内系统保障率最大作为目标函数值。构建模型如下

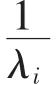
T内的航材需求量服从均值为λiT的泊松分布[9]，即

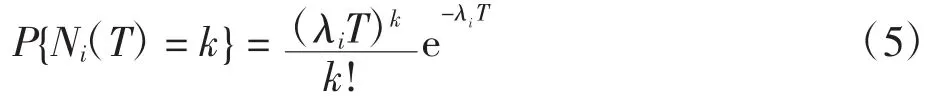
其中

其中：L是某机队该机型飞机数量；H是该机型飞机每日平均飞行时数；Mi是第i种航材在每架飞机上的装机数；MTBURi是第i种航材平均故障拆换时间。由泊松分布叠加性质可知，整个系统的保障率为

2 算法描述

在1.2节的模型中，涉及的变量相对较多，且设备清单中涉及的航材种类较多。若采用边际优化算法计算相对复杂[10]，计算量大、迭代步骤多，因此，选择智能算法进行求解。

2.1 量子粒子群优化算法

在量子力学基础上发展出的量子粒子群的新算法[11]认为，粒子具有量子的特点，即粒子的速度和位置不能同时确定，无需考虑速度因素，而是利用波函数描述位置，且其只有一个参数即收缩扩张系数，与标准粒子群算法相比，该算法相对简单、搜索速度较快、寻优能力强。

在标准的粒子群算法中，最小势能位置为

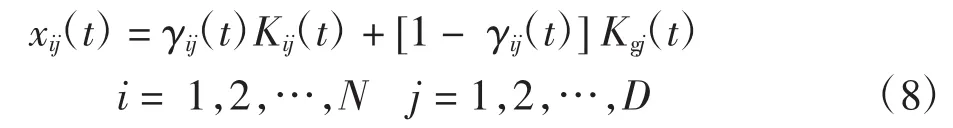
其中：N为种群规模；D为搜索空间的维数；γij（t）为均匀分布在[0，1]的随机数；Ki为个体最优；Kg为全局最优。

利用蒙特卡罗法，在t次搜索后第t+1时所处的位置为

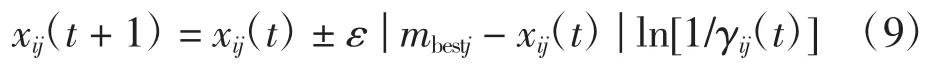
其中：ε为收缩扩张系数；mbest为平均最优搜索位置，即

个体最优与全局最优的更新方程如下其中，g（x）为适应度函数。

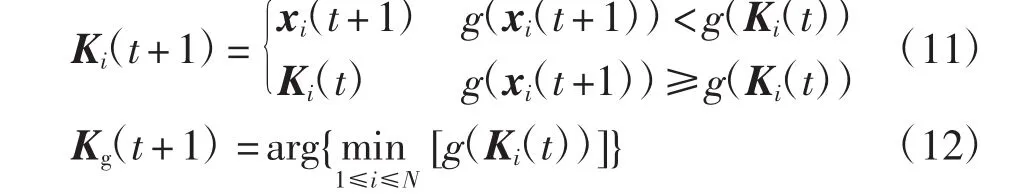
2.2 改进量子粒子群算法

针对量子粒子群存在过早收敛的问题，许多学者在量子粒子群基础上做了一定改进[9，12-14]。在传统量子粒子群算法中，收缩扩张系数ε是线性变化的，但在实际寻优过程中往往是非线性的且具有较高的复杂度[15]，ε应能根据寻优过程实际变化而自适应调整。种群粒子在寻优过程中不断向最优位置靠拢，种群多样性的减少会造成后期陷入局部寻优。因此，引入进化因子μt对mbest进行动态化非线性调整。

2.2.1 收缩扩张系数

收缩扩张系数与传统粒子群中的惯性权值相似，用于计算粒子的适应度。引入动态权值，对收缩扩张系数进行动态化调节，可表示为

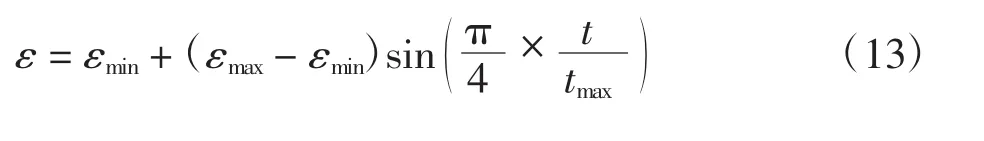
其中，εmax与εmin分别为ε的最大值与最小值。

在搜索初期迭代次数较少时，ε与εmax相近，可保证算法的全局寻优搜索能力；随着后期迭代次数递增，ε以非线性变化递减，可确保局部寻优搜索能力。通过该方法灵活调整全局搜索能力与局部搜索能力间的变化，进而实现一种动态平衡。

2.2.2 mbest的进化因子

针对算法后期搜索易陷入局部最优的问题，引入种群粒子最优平均值mbest的进化因子μt，即

其中：Kt（0，1）和Gt（0，1）分别为基于柯西分布和基于高斯分布在[0，1]范围内产生的随机数；m1、m2为扰动因子，动态变化如下

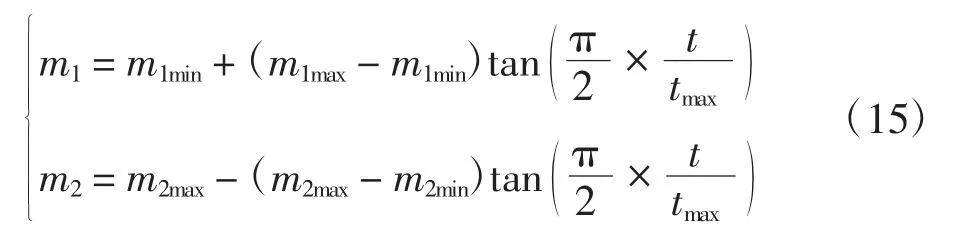
其中：m1max、m1min、m2max、m2min分别为 m1、m2的最大值与最小值；tmax为更新次数的最大值。引入进化因子后，种群粒子平均迭代最优位置为

2.3 模型求解

算法求解过程如下：

1）初始化粒子群，并在标准算法基础上引入式（13）和式（16），对传统量子粒子群中参数进行改进；

2）计算出粒子适应度值；

3）将新粒子的适应度值对比当前最优值，若更优则根据式（11）和式（12）进行更新；

4）根据式（4）判断各变量是否超出其取值范围，若超出，即取其对应的限制，防止其超出可行的搜索区域。

5）根据是否达到最大迭代次数判断是否停止。

3 实例分析

以某航空公司使用的设备清单（表1）为例，验证算法有效性。分别采用PSO、标准QPSO、改进QPSO 3种算法进行求解，种群规模N为20，最大迭代次数为100，在改进QPSO中引入收缩扩张系数ε、进化因子μt，基本参数与QPSO、PSO相同。仿真结果如表2和表3所示，适应度曲线如图1～图3所示。从航材配置数量、购置成本和适应度值来看：3种智能算法均优于首期设备清（RSPL）计算结果，证明了优化的必要性；QPSO和改进QPSO结果优于传统PSO的计算结果，达到了优化的效果。

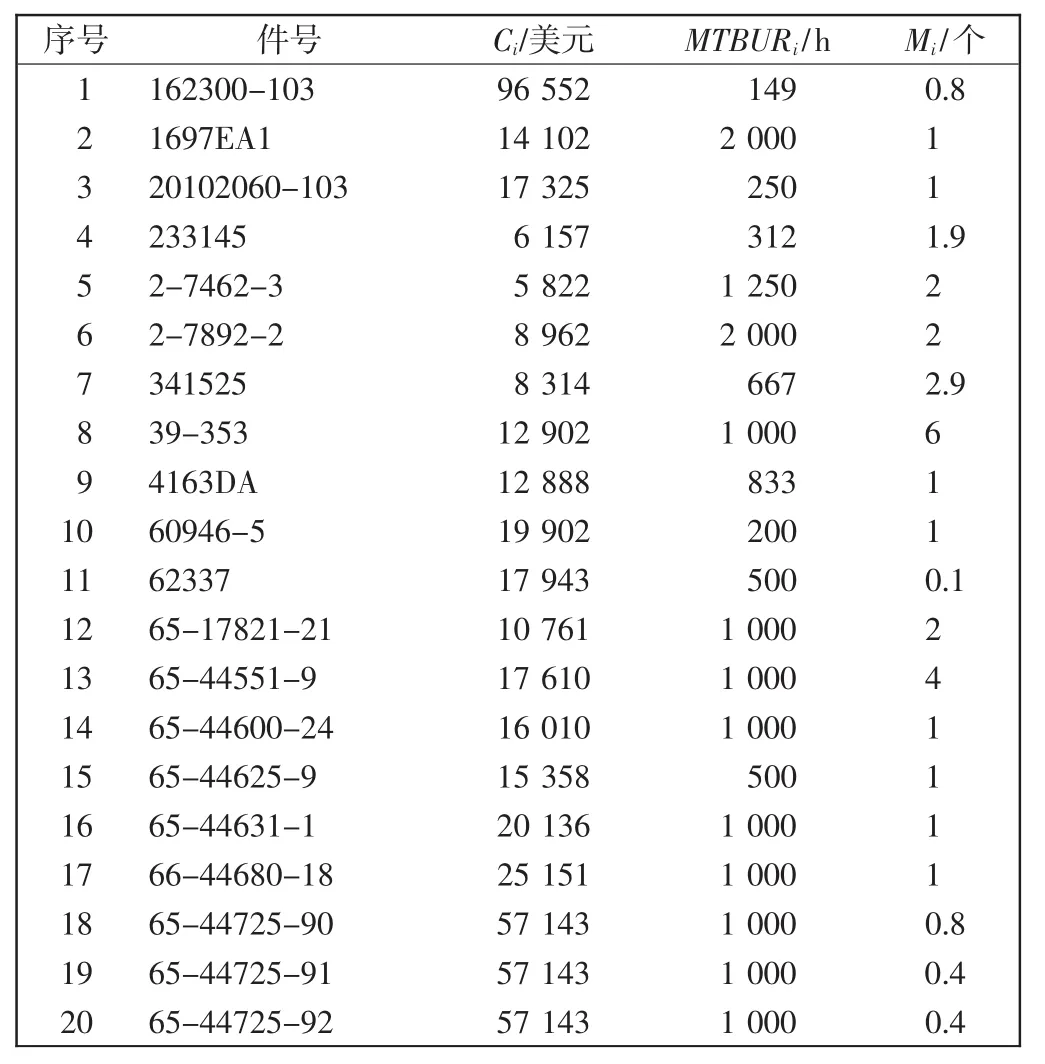
表1 航材参数表Tab.1 Parameter list of aviation spare parts

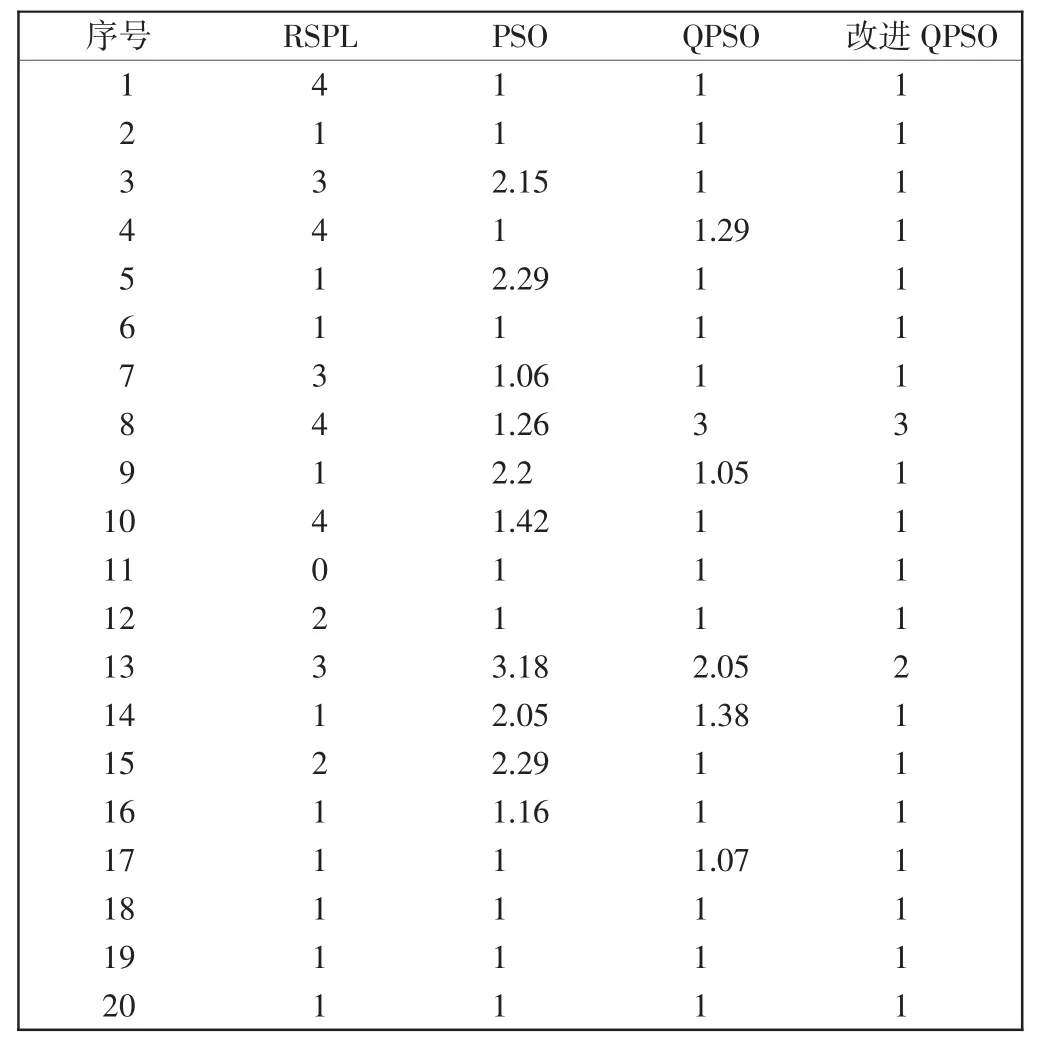
表2 首期设备清单及不同算法航材配置数量对比Tab.2 First stage equipment list and number comparision of aviation spare parts by different algorithms个

分析QPSO与改进QPSO的实验结果如下。在航材配置数量方面，两者结果相近。在购置成本方面，改进QPSO比QPSO节省了约一万美元；在适应度值方面，两者的最大值相同均为1.78×10-6。因此，改进QPSO实现了用更少的投入获取更高的收益，达到了单位最大化的目的。从收敛速率来看，QPSO在38代左右，达到最大值，此后稳定不变，未出现局部收敛和不收敛的情况，而改进QPSO在适应度最大值相同的情况下，迭代速率有明显的提升。

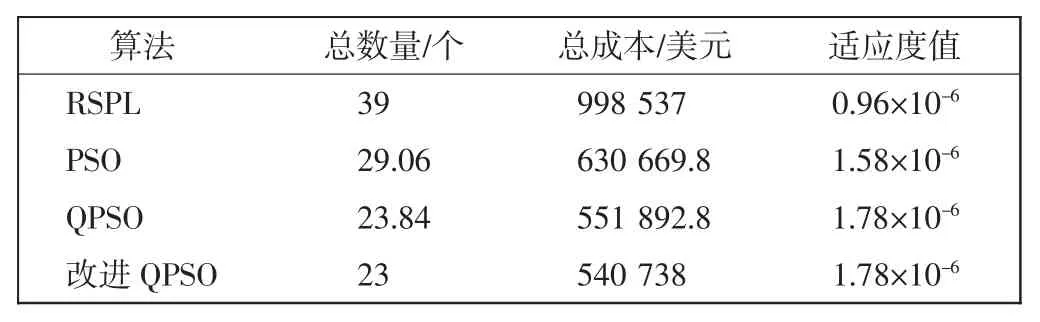
表3 不同算法优化结果对比Tab.3 Optimized result comparision of different algorithms

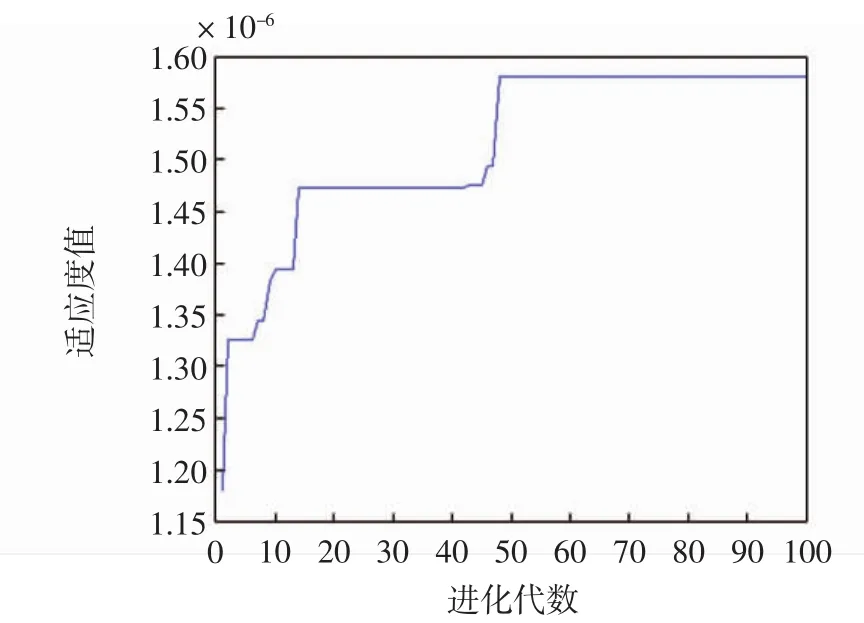
图1 PSO适应度曲线Fig.1 PSO fitness curve

图2 QPSO适应度曲线Fig.2 QPSO fitness curve

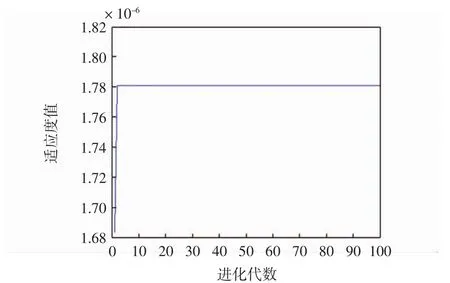
图3 改进QPSO适应度曲线Fig.3 Improved QPSO fitness curve

4 结语

针对量子粒子群优化算法在优化配置中存在过早收敛和全局寻优能力不完美的情况，从收缩扩张系数和进化因子方面进行改进。在目标函数中引入总成本变量，构造出单位成本系统保障率最大模型，将改进的量子粒子群应用在航材初始备件配置优化领域中。通过实验得出，改进的量子粒子群的结果要优于传统粒子群（PSO）及首期设计清单中的结果，在收敛速率上优于QPSO，提高了优化效率，同时节省总的购置成本，可为航空公司在制定首期设备采购策略时提供参考。