基于改进ORB的抗视角变换快速图像匹配算法*

左 川,庞春江

(华北电力大学控制与计算机工程学院,河北 保定 071003)

图像匹配是计算机视觉和数字图像处理等学科领域中十分重要且基础性的技术,已经在机器人视觉[1～2]、目标跟踪[3]和图像拼接[4]等领域得到了广泛应用。基于局部特征的图像匹配算法具有鲁棒性强、灵活性高等特点,是当前研究的热点,备受关注。其中尺度不变特征变换(SIFT)、快速鲁棒性特征(SURF)和快速定向二进制描述(ORB)等算法具有典型性。

ORB[5]相比SIFT与SURF算法具有计算量低,运行速度快等优点,但误点率高、像素对比结果易受噪声影响和抗视角变换能力弱等缺点仍影响该算法在实际工程上的应用。在抗视角变换方面,侯毅[6]等人提出仿射不变的快速定向二进制描述(AORB)算法,利用仿射变换模型模拟视角变化,使算法具备完全仿射不变性。曾庆华[7]等人将透视模型与ORB结合得到抗视角变换的快速定向二进制描述(PORB)算法,并利用随机采样一致性(RANSAC)算法进行误点剔除,使算法保持较高匹配精度的同时具有较好的抗视角变换能力。虽然两种算法提高了ORB的抗视角变换能力,但并未考虑算法本身误点率高和描述符易受噪声影响。在特征描述方面,王强[8]等人对二进制鲁棒独立基本特征(BRIEF)算法进行了改进,利用差分大小与差分幅值生成描述符,降低了噪声的影响。李卓[9]等人利用基于学习的三元组(LATCH[10])二进制描述子进行ORB特征描述,提高了描述符的鲁棒性。以上两种方法提高了描述子能力,但其提取的特征点不稳定,误点率高的问题依然存在。在提高精度方面,秦晓飞[11]等人利用RANSAC和8点改进算法计算基础矩阵,应用极限约束进行精匹配,提高了匹配精度。贺黎[12]等人提出顺序采样评估方法,对初匹配得到的匹配点按汉明距离进行排序采样,利用最小二乘法进行误点的去除,最终连续迭代得到最优匹配点集。以上两种算法提高了匹配精度,但导致算法复杂度提高,实时性降低。

针对以上问题,本文提出基于改进ORB的抗视角变换快速图像匹配算法。对ORB算法进行改进,利用加速分割检测算法(AGAST)进行特征点提取,并提出特征点加速检测策略,提高了特征点稳定性和检测速度,其次利用改进的BRIEF算法提取旋转不变的二进制描述子,同时提高了对噪声的鲁棒性,最后得到改进ORB算法。结合透视变换模型对实时图像进行采样得到模拟图像集,利用改进ORB算法对获取的模拟图像集和模板图片分别提取特征点,根据变换关系分别将模拟图像集特征点映射到实时图像上,并对实时图片和模板图片上的特征点进行特征描述,将汉明距离作为相似度量准则进行初匹配,利用网格运动统计(GMS)算法在初匹配结果的基础上进行提纯,达到误点剔除。

1 传统ORB算法

ORB利用加速分割测试特征(FAST)算法进行特征提取,采用BRIEF算法形成特征点的二进制描述符,利用汉明距离作为相似性度量准则进行描述符比较。算法主要步骤:

①特征提取:利用FAST算法进行特征点提取,灰度质心法为特征点提供方向。特征提取速度快实时性高,但FAST算法利用ID3进行决策树构建,提取的特征点绝大程度上属于局部最优解,导致特征点的误点率较高。

②特征点描述:利用BRIEF算法进行特征点描述。在以特征点为中心的邻域内取n个点对,并进行灰度值的比较,形成0/1二进制描述符。同时描述子不具有旋转不变性,因此将特征点主方向应用到点对矩阵上得到旋转不变矩阵,最终得到旋转不变的二进制描述子。该算法灰度值的比较易受噪声影响,ORB算法通过高斯平滑可以缓解噪声问题,但会造成较多特征所在的高频区域信息缺失,在得到旋转不变描述子的过程中计算复杂度较高。

③特征匹配:利用汉明距离作为相似性度量,同时根据最近/次近原则对二进制描述符进行比较判断。汉明距离是相同位数的二进制串中对应位不同的数量,该数量代表二进制描述符的相似性程度。计算机通常使用异或操作得到汉明距离。在匹配时,如果两个关键点的最短与次最短的距离比小于0.5,认为这两个点匹配成功。这种匹配方法,简单易行,计算速度快。

2 改进ORB算法

针对ORB算法的不足,本文在两方面提出了改进,①特征提取:采用AGAST算法提取特征点,并提出特征点加速检测策略,提高了特征点稳定性和检测速度;②特征描述:采用改进BRIEF算法进行特征描述,使其具有旋转不变性和更好的噪声鲁棒性。

2.1 AGAST算法

AGAST是在FAST算法基础上改进得到的算法,与FAST 算法使用ID3构建决策树不同,AGAST算法构建最优二叉决策树,中心像素与周围8个像素灰度值比较结果如式(1):

(1)

构建尺度空间。设原始图像尺度为t1(0)=1,下一尺度为为t1(i)=2i,两个尺度空间中有一个分数尺度空间t2(i)=2i×1.5。因此,整数层尺度空间t1(i)=2i,i=0,1,2,3,…和分数层尺度空间t2(i)=2i×1.5,i=0,1,2,3,…构成了本文的图像金字塔。利用尺度空间生成不同尺度的图像后,AGAST算法分别对不同尺度图像进行特征点检测,同时在图像以及各个尺度层应用NMS(非极大值抑制)求取局部极值。

针对图像金字塔层与层比例为2的特性,本文提出了特征点加速检测策略:利用AGAST5-8算法在较大尺度空间上进行检测,若检测一点为特征点,则使用AGAST9-16算法检测较小尺度空间中该点对应点3×3邻域的特征点。如下图为检测模板。注:P为中心点,AGAST5-8与FAST5-8原理一样,中心点P与其周围8个点比较,连续5个点灰度值均大于或者小于P点灰度值,则中心点P为特征点,AGAST8-16同理。

图1 AGAST5-8模板(深色)与AGAST8-16模板(浅色)

如t1(i)尺度下,利用AGAST5-8检测到特征点位置(x,y),则在t1(i-1)尺度下使用AGAST9-16对x′∈{2x-1,2x,2x+1}和y′∈{2y-1,2y,2y+1}的邻域进行特征检测。特征点加速检测策略速度的提高由于:第一,较大尺度图像的尺寸是较小尺度的四分之一,利用AGAST5-8检测模板直接排除较大尺度上的平坦区域,这使得较小尺度上利用AGAST9-16模板检测的像素数量减少;第二,AGAST5-8决策树的深度远小于AGAST9-16决策树深度,使得AGAST5-8模板进行预先检测计算量较小,达到整体检测耗时较短。

本文采用灰度质心法为特征点提供方向。特征点作为邻域中心,其灰度矩:

(2)

式中:I(x,y)表示特征点(x,y)处的灰度值,q,p代表灰度矩的阶数。因此灰度矩心:

(3)

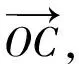
θ=arctan[2(m01,m10)]

(4)

2.2 改进BRIEF描述算法

BRIEF描述算法不具有旋转不变性并易受噪声影响。ORB算法虽然根据高斯分布,在特征点邻域随机选择5×5的窗口,并进行平滑处理得到灰度积分,使用窗口的比较来代替像素点对的比较,同时将特征点的主方向应用于描述子上。但高斯造成了特征区域信息的缺失,借助特征点主方向对每一个特征点对矩阵进行旋转,造成计算量增加。

针对以上不足,本文提出改进BRIEF算法,以特征点为中心的15×15邻域为特征描述区域,在邻域内利用3×3的模板进行取点,共取25个点,点集P={p,p1,p2,…,p24},其中p为中心特征点,pi,i=1,2,…,24为邻域内描述子点。如图2所示。借鉴LOOP[13]思想,本文分别以中心特征点和各个描述子点为中心,对各个点3×3的邻域内进行式(5)计算,得到每个小区域的二进制描述符。这种取点方式在计算复杂程度上要低于传统BRIEF随机取点方式,25个点的数目相比256组点对更是快速,同时每个点的3×3邻域组成的特征描述符涵盖了特征区域15×15的全部像素点,降低了信息冗余。

图2 描述子点分布图

(5)

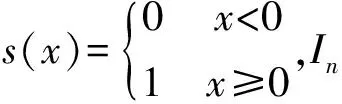
如图3(a)所示,对pi利用式(5)计算,旋转前后的二进制描述符存在差异,这对于图像出现旋转时导致匹配精度大幅下降。图3(b)所展示为改进后的算法,如式(6),旋转前后的二进制描述符不变。

(6)

式中:KIn为在pi邻域中In在中心点pi周围8个像素中的灰度值排序。在进行灰度值比较前,先对8个像素灰度值进行由小到大排序得到集合K,每个灰度值与平均灰度比较时,其位置权重为该像素在集合K中的位置,而不是简单的顺时针排序分配权重。这样保证了当区域发生旋转变化时其像素灰度值的排序不受旋转变换的影响,从而使得pi区域的二进制描述子不变,具有旋转不变性。

中心特征点p的15×15邻域取点集合为P={p,p1,p2,…,p24},分别中心特征点p和各个描述子点pi进行式(6)运算得到每个区域的二进制描述,并按点集顺序将描述符拼接形成特征点p的特征描述符。每个小区域的描述符具有不变性,所以得到的特征点描述符具有旋转不变性。每个特征区域取点25个,形成25 byte的特征描述符。相比传统BRIEF算法得到的32 byte,在形式上更简洁,计算复杂度更低。

3 基于透视变换模型和GMS的改进ORB算法

为了具有抗视角变换能力和匹配精度更高,本文构建透视变换模型模拟相机视角变换,同时初匹配之后利用GMS算法进行精匹配,达到误匹配点的剔除。

3.1 建立透视变换模型

本文搭建透视变换模型,使ORB算法具有抗视角变换能力。

根据针孔相机成像原理可知,输入图像中a点和模拟图像a′点存在如下关系。

(7)

式中:K、R和t分别代表固有矩阵(根据相机参数获取)、旋转矩阵和平移矩阵(根据模拟相机在世界坐标系位置得知)。旋转矩阵是根据模拟相机的坐标系相对于世界坐标系计算得到的,并且式(7)中取旋转矩阵的前两列。H为单应性矩阵,反映了输入图像与模拟图像的映射关系。

建立坐标系,如图4,透视相机模型的具体几何说明。

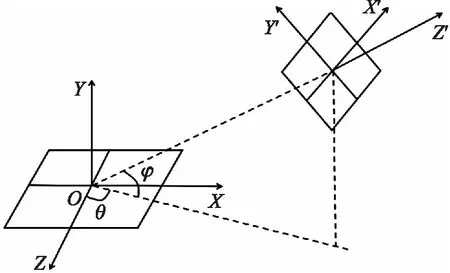
图4 相机模型几何说明

相机光轴Z′绕Z轴逆时针转动,角度取γ,其在平面XOZ投影与Z轴夹角为θ,同时与平面XOZ的夹角为φ,相机到世界坐标系原点距离为r。因此,式(7)中的平移矩阵可由相机在世界坐标系的位置表示T=[rcosφsinθrsinφrcosφcosθ]T。旋转矩阵由于相机光轴总是对准世界坐标系的原点并且是由3个方向的旋转矩阵构成,可表示为:

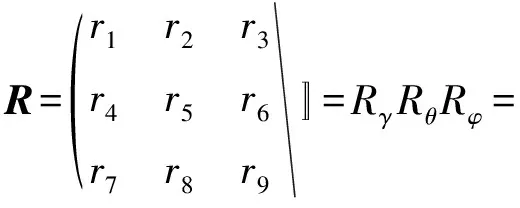
(8)

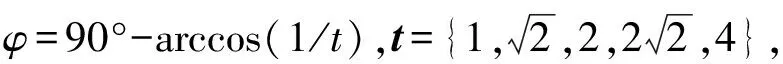
3.2 GMS算法的误点剔除

基于网格的运动统计[14](GMS算法)是一种将运动平滑度封装为区域内匹配点数目,通过阈值比较区分匹配正确与否的算法,从而获取正确匹配,消除错误匹配。

初匹配后得到模板图像I1到实时图像I2的匹配点集X,Si为匹配点xi∈X周围邻域中匹配得分以及分布情况。

(9)

式中:|Xakbk|为匹配点对对应领域区域中匹配点个数。K为不相交区域的个数,使得算法具有多邻域泛化能力。Si分布属于二项分布,n为匹配点邻域特征点个数,pt和pf分别为正确匹配概率与错误概率。mt、mf、st和sf分别为xi为正确/错误匹配点下Si的均值和标准差。如此得出其分布图,并基于阈值τ划分。

图5 Si分布图

为了实现具体计算和降低复杂度,GMS算法将输入的两图像各自分为不重叠的20×20网络。原来计算每个特征匹配点邻域Si得分的复杂度O(N),N点集X的数目,通过计算网格对的匹配分数Sij,如式(10),只计算一次,使复杂度为O(1),大大提高了算法的执行效率。

(10)

式中:|Xikjk|为两图像网格对的匹配点数目,K为9,Sij为将网格i和j及各自周围的8个区域分别计算并求和得到。

(11)

a=6,ni为K=9个区域的特征点平均值。因此通过Sij与τi比较得出正确匹配网格对。

3.3 算法实现步骤

Step 1 输入模板图像I1和实时图像I2;

Step 2 利用搭建的透视变换模型对实时图像进行变换,得到模拟图像集合;

Step 3 利用改进的ORB算法对I1和模拟图像集中的图像分别进行特征点检测,并根据映射关系,将检测到模拟图像集的特征点映射到I2上;

Step 4 利用改进的ORB算法对两图像上特征点进行特征描述;

Step 5 利用汉明距离作为相似度量准则进行初匹配;

Step 6 将初匹配后的两个图像分别划分20×20的网络;

Step 7 对I1上的i网格在I2上匹配到使Xij数最大的j,i,,j∈[1,20×20];

Step 8 计算Sij和τi;

Step 9 比较Sij与τi,如果Sij大于τi,则XT=XT∪Xij,i+=1,返回step 7;否则,j+=1,返回step 7;

Step 10 得到正确匹配点集XT,输出匹配图像。

4 实验分析

为了验证所提出的算法的有效性,本文将对AORB[6]、PORB[7]和本文所提算法分别从尺度和旋转不变性、抗视角变换性和运行耗时三方面进行实验。硬件环境:Intel(R)Core(TM)i7,CPU 2.80 GHz,RAM:8GB;软件环境:Window7操作系统,VS2010和OpenCV2.4.9。实验数据采用Mikolajczyk标准数据集和MorelYu数据集中存在尺度、旋转和视角变换的图像集。评价标准为匹配精度,即(匹配正确点数/匹配点总数)*100%。匹配正确点数和总点数由随机抽取一致性算法(RANSAC)获取,该算法从OpenCV函数库中直接调取,阈值2,置信度0.99。

4.1 尺度和旋转不变性对比实验

对于尺度和旋转对比实验图像集采用Boat图像集,共6幅图像,如图6所示。采用匹配精度曲线图作为尺度和旋转不变性实验的评价标准。

图6 尺度旋转实验

由图6可知,在相同尺度旋转变化情况下,本文算法的匹配精度高于AORB和PORB算法,这是因为本文算法使用AGAST算法提取的特征点相比于AORB和PORB中FAST算法提取的特征点具有更强的稳定性兼具尺度不变性,同时改进的BRIEF算法对特征点邻域取点分别得到旋转不变的二进制描述子并且降低了局部区域对噪声的敏感性,使得整个特征点描述子具有更强的旋转不变性和对噪声的鲁棒性。同时本文构建了尺度空间,加强了本文算法在尺度变换的匹配能力。因此,本文算法提高了尺度和旋转不变性能力。

4.2 抗视角变换对比试验

对于抗视角变换对比实验图像集分别采用:纬度是唯一变量,视角逐渐增大的Graffiti图像组,共6幅;只改变纬度,图像尺度不变的Magazine-zoomx4、painting-zoomx1和painting-zoomx10图像集,分别为9幅、5幅和5幅;纬度不变,只改变经度的Magazine-t2图像集,共10幅。采用匹配精度作为抗视角变换对比试验的评价标准。图7为本实验结果,其中的柱状图纵坐标为正确匹配点的数量,折线图分别为各组实验中图像匹配精度的变换曲线。

图7 抗视角变换实验

从不同组别的柱状图和曲线图可知,本文算法得到的正确匹配点数目高于AORB和PORB。由精度曲线数据计算5组数据的平均匹配精度,本文算法89.11%均高于AORB的73.77%和PORB的84.53%。

本文算法利用透视变换模型进行图像模拟,在视角模拟上要优于AORB使用的仿射变换模型,从而使得本文算法在抗视角变换能力上高于AORB算法。相比同样使用透视变换的PORB算法,本文算法提出改进的ORB利用AGAST进行特征点检测,比传统ORB检测到的特征点具有更多的数量和更强的稳定性,同时改进的BRIEF算法充分利用了特征点区域的信息,增强了描述子的稳定性和对噪声的鲁棒性,使得的匹配点数目更多,经过GMS精确匹配保留了更多的正确匹配点。PORB算法使用传统的ORB算法得到匹配点对,但误点率高和点对中存在过多的误匹配点,虽然利用RANSAC计算图像间的单应矩阵弥补了图像模拟带来的误差和去除误匹配点,但使得最终得到的正确匹配点对和匹配精度均要低于本文算法。因此,本文算法相比于AORB和PORB,具有更好的抗视角变换能力和更高的匹配精度。

为了验证本文算法的有效性,取手机拍摄的两张现实生活中图片进行验证,如图8展示。匹配正确点数目分别为284和376,匹配精度为91.63%和95.48%。

图8 数据及本文算法匹配结果

4.3 运行耗时对比试验

运行耗时对比实验数据是前两节实验中每组实验耗时计算的平均时间。

由表2可知,本文算法的运行耗时均小于AORB和PORB算法,平均耗时较两种算法分别提高了9.70 s和4.73 s。与PORB相比,两算法虽然都采用透视变换模型和使用传统的图像匹配流程,但本文对ORB提出了改进,AGAST算法本身在提取特征点速度上快于FAST算法,并且本文提出了特征点加速检测策略,进一步提升了检测效率。改进的BRIEF算法,降低了描述子的信息冗余,并且描述子为25 byte,较32 byte的PORB描述符更简洁,特征匹配更快。使用GMS算法进行误点的剔除,该算法,通过计算特征点邻域的得分,来判断是否为正确点,并且通过采用网格划分模式进行算法的加速,使算法复杂度为O(1)。相比PORB使用复杂度较高的RANSAC进行误点剔除,效率上得到了大大的提升。AORB采用仿射变换模型,使用传统ORB进行特征匹配,利用极限约束进行精确匹配,但是该算法对输入的两张图像分别进行采样并匹配,大大增加了图像数量,致使运行耗时严重高于本文算法。因此相比于AORB和PORB,本文算法运行耗时短,实时性高的特点。

表2 运行时间对比

5 结论

针对ORB图像匹配算法误点率高、像素点对对比易受噪声影响同时抗视角变换能力较弱。本文提出一种基于改进ORB抗视角变换的快速图像匹配算法。该算法在ORB算法的架构下利用AGAST算法进行特征提取,并提出特征点加速检测策略,利用改进的BRIEF算法进行特征点的描述,同时结合透视变换模型对图像进行透视采样和汉明距离作为相似度量准则进行图像匹配,最后利用GMS算法去除误匹配点。通过与AORB和PORB算法实验对比,本文算法在拥有较强尺度旋转不变性和抗视角变换能力的同时,具有更高的匹配精度和更好的实时性。下一步主要将算法融入机器人视觉系统和深入研究探讨工程应用价值。