概化理论与项目反应理论的融合模型

(华南师范大学心理学院、心理应用研究中心,广州 510631)

1 引 言

概化理论(generalizability theory,GT)和项目反应理论(item response theory,IRT)都是现代心理与教育测量理论，广泛应用于心理与教育测评实践中。概化理论和项目反应理论可以对划界分数的标准误进行估计(Lee & Lewis,2008;Christ,Riley-Tillman,Chafouleas,& Boice,2010;Wu & Tzou,2015)，也可以应用于表现性评价(Clauser,Harik,& Margolis,2006;Casabianca,Mccaffrey,Gitomer,Bell,Hamre,& Pianta,2013;Meyer & Mashburn,2014)、体育测试(Coleman & Epstein,1998)、评分考试(Lakin& Lai,2012;朱宇,冯瑞龙,辛涛,2013;Clauser,Margolis,& Clauser,2014)、认知评估(Yin & Shavelson,2004,2008;余嘉元,2011)、学生评价(Casabianca,Lockwood,& Mccaffrey,2014)、教师评价(黎光明,张敏强,2017;王幸君,黎光明,张敏强,蒋欣,梁正妍,楚肖依,2016)、情绪测量(Tobar,Stegner,& Kane,1999;魏欢,陈维,韦嘉,张进辅,2017)、人格测验(Salter,Forney,& Evans,2005)及评价者“漂移”(rater drift)(Harik,Clauser,Grabovsky,Nungester,Swanson,& Nandakumar,2009)等。

然而，概化理论和项目反应理论都存在着一些不足：一是概化理论微观分析能力不强，对于不平衡数据和不完整数据处理能力有限(Brennan,2001;Choi,Briggs,& Wilson,2009)；二是项目反应理论的强假设(单维性、局部独立性和单调性)在实际中难以满足，在一定程度上限制了其在心理与教育实践中的应用(Choi,Briggs,& Wilson,2009;戴步云,张敏强,焦璨,黎光明,朱华伟,张文怡,2015)。概化理论更多关注宏观层面的技术(如对信度和效度的探讨等)，较少关注微观分析(如对项目质量进行分析等)，这不利于心理与教育测量进行更为具体的微观分析，如分析某些评价者过严、某些项目过难等。项目反应理论则要求所考察的特质具有单维性、独立性和单调性等，这些都在一定层面抑制了它的宏观应用。

为了兼顾宏观层面和微观层面的应用，概化理论和项目反应理论宜从以下两方面进行改进：一是两种理论相互补充、相互整合，互相吸收各自的微观技术和宏观技术，如项目反应理论可吸收概化理论宏观技术，而概化理论可吸收项目反应理论的微观技术等；二是对概化理论和项目反应理论进行有效整合，从而确立一种更加广义的概化理论和项目反应理论，并兼有概化理论和项目反应理论两种理论优势，博采众长，融合成一种新的理论或模型。

促成概化理论与项目反应理论进行整合，有两种途径可以实现：一是同时对一批数据进行概化理论分析和项目反应理论分析，得出一些具体指标(Lee & Lewis,2008;Lee & Park,2012;Smith & Kulikowich,2004;Zhong,Kang,& Chen,2013;俞宗火,唐小娟,王登峰,2009;徐思,张敏强,黎光明,2009)，可称为“黏合”；二是将概化理论与项目反应理论进行实质性地整合，可称为“融合”，产生一种新的理论或方法或模型对一批数据进行概化理论分析(Marcoulides,1999;Briggs & Wilson,2007;Chien,2008;Choi,Briggs,& Wilson,2009;Li,2009;Choi,2013)。

概化理论与项目反应理论的“黏合”与“融合”的区别在于：前者并非实质性整合，仅仅是两种理论分开来对数据分别进行分析；后者是实质性整合，需要诞生出新的融合模型。

2 概化理论与项目反应理论的“融合”优势

第一，将概化理论与项目反应理论进行“融合”，有利于深化概化理论和项目反应理论的研究，能够为创造性地产生一种新理论或新模型奠定基础。概化理论是一种线性模型，其原理是通过分解总方差分量来探讨不同测量侧面对测量目标的影响，是一种宏观层次的理论(Fan & Hansmann,2015;Wan,Fan,Yang,Pan,& Chen,2014;Ziegler,Poropat,& Mell,2014)。项目反应理论是一种量表化模型，是一种微观理论，重在对题目参数和能力参数进行估计。项目反应理论涉及一些复杂的统计计算，如参数估计等，还面临着一些不能处理的假设条件。如何将项目反应理论的适用范围进一步扩大，是项目反应理论必须解决的问题。

第二，将概化理论与项目反应理论相结合，可以深化概化理论和项目反应理论研究，为两种现代测量理论走向大统一提供重要的方法指导，也可以为概化理论和项目反应理论融合后产生新模型进行后续方法研究提供基本保障。在项目反应理论模型中，第一层描述的是项目的log-odds和正确反应，第二层则定义了考生的能力，可以是多级效应模型。概化理论沿着随机样本理论和线性模型的思路向前发展，着重讨论实测时的测量条件与结论推广应用范围之间的关系，也可以是多级效应模型。鉴于概化理论和项目反应理论都可以是多级随机效应模型，抽样模型概化理论可以被纳入扩展至项目反应理论量表化模型中。

第三，将概化理论和项目反应理论进行有效的“融合”，更具技术性，实现起来相对困难，但却代表未来现代测量理论的发展趋势。一些学者已将概化理论与项目反应理论进行了有效整合，并产生了概化理论与项目反应理论的融合模型(Kolen & Harris,1987;Briggs & Wilson,2007;Chien,2008;Choi,Briggs,& Wilson,2009;Li,2009;Choi,2013)。概化理论与项目反应理论的融合模型，使得两种理论能够取长补短，并使得概化理论和项目反应理论的应用前景更加光明。

3 概化理论与项目反应理论的融合模型

目前，一些学者对概化理论与项目反应理论实质性结合的“融合”模型进行了介绍，总结文献，可分为以下几类：

第一，多变量建模方法(MM)。Kolen和Harris(1987)提出了多变量建模方法(multivariate modeling，MM)，该方法假定所观察到的测试成绩方差在GT中可以分解成不同方面的贡献，而方差分量模型为IRT的条件概率密度函数。Kolen和Harris指定MM方法项目特征函数为p(ypi=1|θp,ζi)。p(ypi=1|θp,ζi)，为一个三参数logistic项目反应模型，如下。

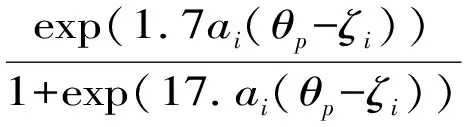
(1)

在公式(1)中，Kolen和Harris假定θp与ζi服从正态分布，而判别参数ai和猜测参数c遵循β分布。为了简化计算，Kolen和Harris将分布的项目和个人参数进行离散化，用离散分布替代积分求和，并使用方差分量来估计概化系数。不像概化理论模型，Kolen和Harris提出，可以用多变量建模方法将概化理论与项目反应理论相融合，多变量建模方法是在人和项目参数局部独立性假设条件下进行的。MM方法既吸收了概化理论的假设条件，也吸收了项目反应理论的假设条件。MM方法所建立的数学模型类似于概化理论方差分量模型。MM适合于一般形式的测验，测验的题型仅包括二值记分题，且题目之间是相互独立的，如某些学绩测验(仅包含选择题题型)、智力测验(如瑞文渐进测验)等。

第二，等级评分模型方法(HRM)。Patz,Junker,Johnson和Mariano(2002)提出了一种融合GT和IRT的新模型，即等级评分模型(hierarchical rater model，HRM)。Patz等人关注的是p×i×r研究设计下的GT模型与IRT中FACETS模型的融合。当多个评定等级存在一个项目反应时，HRM方法的关键特征是获得“理想的评级”ζpi。ζpi将p和i的真实分数对应在GT中。该模型假定所观察到的数据是由两阶段随机过程产生的，如下：

第一阶段，构建IRT模型：

logit(p(ζpi=ζ|θp,βi,τiζ,Xpik{ζ,ζ-1}))=θp-βi-τiζ

(2)

在公式(2)中，HRM方法假定人的能力θp和难度βi服从正态分布，τiζ表示第ζ步第i个项目的分部评分，其中βi-τiζ的均值被限制为零。

第二阶段，构建GT模型：

ppikζs=p(Xpik=s|ζpi=ζ)∝exp

(3)

在公式(3)中，ppikζs表示第ζ步i项目中的p的反应概率函数。ppikζs构建出GT的模型，包括测量误差的不同来源。模型参数估计使用马尔可夫链蒙特卡洛方法(Markov Chain Monte Carlo)，即MCMC方法。当项目的影响被认为是固定在人和评分者中时，HRM是有用的。然而，HRM不能提供估计的概化系数，因为方差分量的大小变化取决于潜在的熟练程度和理想的评定等级。HRM适合于具有等级评定的测验，如心理评定量表等，评定的等级可以是二级，也可以是多级，但题目之间是相互独立的。

第三，项目反应下的概化模型方法(GIRM)。Briggs和Wilson(2007)通过对概化理论中的测量侧面进行分布假设，提出了GT和IRT相融合的项目反应下的概化模型(generalizability in item response modeling，GIRM)。与传统GT方法使用观测分数矩阵(observed response matrix)计算方差分量不同，GIRM模型使用MCMC方法来估计IRT中的参数，并使用期望分数矩阵(expected response matrix)来估计各种方差分量。Briggs和Wilson的研究结果显示，GT和IRT结合的技术能够对方差分量进行准确的估计。另外，因为GIRM模型是在期望分数矩阵的基础上估计各个方差分量，所以GIRM模型可以分离交互效应和残余效应。GIRM模型不受缺失数据的影响。GIRM模型诸多性能是传统GT和IRT方法所不能及的。Briggs和Wilson在模拟数据和实测数据的研究结果显示，GIRM模型和传统GT方法计算所得的各项结果都非常接近，包括对方差分量的估计、概化系数以及可靠性指数的计算。另外，Briggs和Wilson的研究结果还发现，运用不同参数分布形态生成的数据对研究结果并不造成影响。GIRM适合于一般形式的测验，测验的题型可以较多，包括二值记分题，也包括非二值记分题，但题目之间是相互独立的，如某些智力测验、特殊能力测验等。

第四，题组项目反应下的概化模型方法(GIRMT)。在Briggs和Wilson(2007)研究的基础上，一些学者(Chien,2008;Choi,Briggs & Wilson,2009;Li,2009)将GIRM扩展到题组情形中，发展出题组项目反应下的概化模型(generalizability in item response modeling for testlet，GIRMT)。Choi,Briggs和Wilson所构建的GIRMT假定题组具有一定的相互关联，不再遵从IRT独立性假设，但基本思想和算法仍同GIRM方法。GIRMT方法拓展了GIRM方法，其数学模型不再是单维IRT模型，而是多维IRT模型。基于p·×i。设计，GIRMT利用多元概化理论估计方差分量及概化系数。Chien(2008)在其博士论文中提出，可以将GIRMT从p×i设计扩展到p×(i∶h)设计。Chien认为，由于被试的正确作答概率可以被定义为被试的期望分数，也就相当于经典测量理论中的真分数以及GT中的总均值，基于此便可把IRT和GT联系起来。Li(2009)基于项目反应理论和概化理论也提出了题组测试分析的信息矫正方法，这也算是对两种测量理论相融合技术的探索。GIRMT适合于题组形式的测验，如包含有英语阅读理解题的英语水平测验，英语阅读理解题的内容下面可能有较多道题目，题目之间不是相互独立的，是相互关联的。

第五，其他方法。Linacre(1989,1993)建议GT和IRT进行分析时，有必要进行互相补充。Linacre例举了一个包含三侧面的例子，说明了在使用GT的原始评分表和IRT的FACETS模型的Logit量表时，GT和IRT可以同时进行分析。Linacre建议，研究人员选择GT或IRT，或两种都选，需要取决于分析的目的，有两种情况可供选择：一是使用GT的兴趣更多在于获取组别的水平在原始分数量表的分数拓广；二是使用IRT的兴趣则更多在于从侧面的特殊性和从固定的实验设计中独立地估计被试水平。许多研究者遵从Linacre的建议，既使用GT模型分析数据，也使用FACETS模型分析数据(Verhelst & Glas,1993;Bock,Brennan,& Muraki,2002;Lee & Lewis,2008;Smith & Kulikowich,2004;俞宗火,唐小娟,王登峰,2009;徐思,张敏强,黎光明,2009)。Bock，Brennan和Muraki(2002)建议，进行GT和IRT整合分析时，需要注意两种理论对相同定义的不同理解。

4 概化理论与项目反应理论的融合模型比较

根据上述对这些模型方法的介绍，可以对它们的特点进行加以比较，其结果如表1所示。

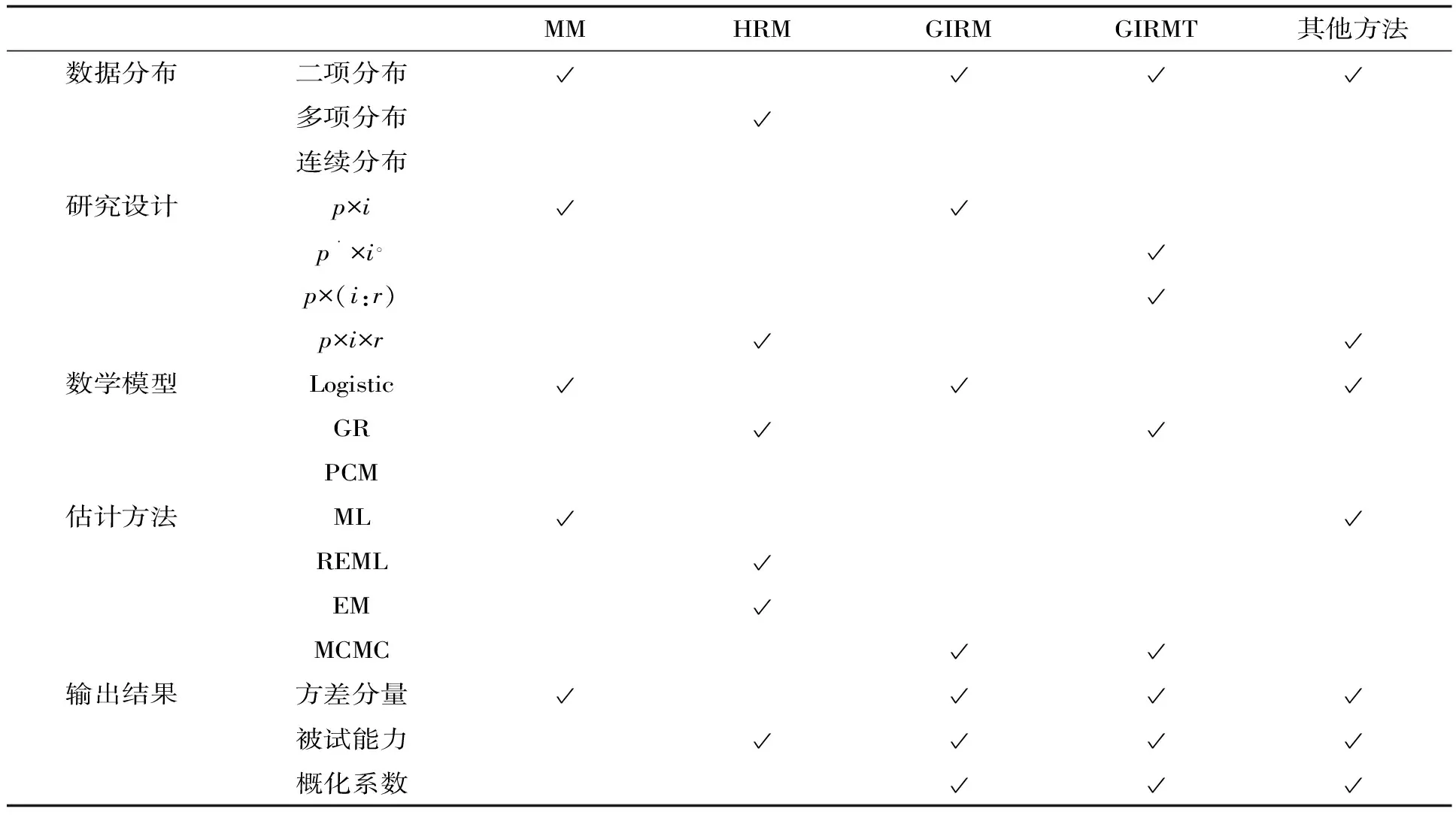
表1 MM、HRM、GIRM、GIRMT及其他方法模型比较

从表1可知，MM考虑了二项分布数据，研究设计为p×i设计，数学模型为Logistic模型，估计方法为ML方法，输出结果只有方差分量。HRM考虑了多项分布数据，研究设计为p×i×r设计，数学模型为GR模型，估计方法包括REML和EM方法，输出结果只有被试能力。GIRM考虑了二项分布数据，研究设计为p×i设计，数学模型为Logistic模型，估计方法仅包括MCMC方法，输出结果包括方差分量、被试能力和概化系数。GIRMT考虑了二项分布数据，研究设计包括p·×i。和p×(i∶r)设计，数学模型为GR模型，估计方法为MCMC方法，输出结果有方差分量、被试能力和概化系数。对于其他方法，考虑了二项分布数据，研究设计仅囿于三侧面交叉设计，所使用的方法为ML方法，数学模型为Logistic模型，输出结果包括方差分量、被试能力和概化系数。

5 概化理论与项目反应理论融合模型研究存在的问题

目前，国内外有关概化理论与项目反应理论融合模型的研究仍存在着一些问题，如下：

第一，所考虑的数据分布或数据类型较为有限。一些提出的概化理论与项目反应理论融合模型及方法所考虑的数据分布或数据类型较为有限，有些研究仅考虑二分数据(Kolen & Harris,1987;Briggs & Wilson,2007;Chien,2008;Choi,Briggs,& Wilson,2009)，有些研究仅考虑非二分数据(Linacre,1993;Bock,Brennan & Muraki,2002;Patz，Junker，Johnson & Mariano,2002)。Kolen和Harris(1987)认为，将GT和IRT进行融合的基石是利用GT的方差分量和IRT的反应函数进行建模，数据类型只能限制于二分数据，不太适合多级数据。Kolen和Harris提出，宜将多级数据进行离散化，把多级数据变成二级数据。另外，Briggs和Wilson(2007)、Chien(2008)以及Choi,Briggs和Wilson(2009)对数据的类型也是二分数据(二项分布数据)。但是，有些学者也认为将GT和IRT进行融合，数据也可以是多级数据(Bock,Brennan & Muraki,2002;Patz,Junker,Johnson & Mariano,2002)。例如，Patz，Junker，Johnson和Mariano等人(2002)认为，将GT和IRT进行融合的数据类型(或数据分布)，不仅可以是二分数据，也可以是多级数据。目前，国外学者提出的将概化理论与项目反应理论融合的大多数模型及方法，仍然没有发展出能够同时处理连续变量和离散变量的方法，也没考虑如何处理缺失数据和不平衡数据。然而，缺失数据和不平衡数据也是数据类型或数据分布需要考虑的一个重要方向，这是因为在日常生活及各种心理调查、心理实验中，不平衡数据和缺失数据随处可见(Allison,2002)。

第二，所建构的数学模型不够全面。将概化理论与项目反应理论进行融合的模型及方法所建构的数学模型不够全面，主要表现在大多数研究所建构的数学模型仅囿于IRT的二值模型(Logistic模型)(Kolen & Harris,1987;Briggs & Wilson,2007;Chien,2008;Choi,Briggs,& Wilson,2009)，仅有少数研究构建了IRT的多值模型(Bock,Brennan& Muraki,2002;Patz,Junker，Johnson &Mariano,2002)。Patz，Junker，Johnson和Mariano(2002)考察了IRT的等级反应模型(Graded Response model，GR)，而Bock,Brennan和Muraki(2002)考察了IRT的分步部分模型(Partial Credit Model，PCM)。Patz等人的等级评分模型方法(HRM)，被看作是一个改良的GT模型和一个改进的IRT模型相融合，模型适合等级反应模型，评定等级定义在一个理想的有序空间的量尺上，并采用预先设定的等级概率估计被试能力。但是，Patz等人所建构的HRM数学模型不够全面，没有考虑其他IRT模型的适用性。Bock，Brennan和Muraki(2002)基于分数评分的阶段性，考察了GT研究设计下的IRT的分步部分模型，但没有考察其他IRT模型的适用性。

第三，所进行的研究设计相对单一。国外学者提出的将概化理论与项目反应理论融合的模型及方法所进行的研究设计相对单一，有些研究仅考虑单侧面设计p×i设计或p·×i。设计(Kolen & Harris,1987;Briggs & Wilson,2007;Choi,Briggs,& Wilson,2009)，有些研究虽然考虑了多侧面设计，如Chien(2008)考虑了双侧面设计p×(i∶h)设计，但没有考虑其他设计，显得不足。常见的概化理论研究设计既包括交叉设计，也包括嵌套设计，还包括混合设计，既可以考虑一个侧面，也可以考虑多个侧面，如p×i、i∶p、p×i×r、p×(i∶r)、i∶(p×r)、i∶p∶r等(Feng,2002;Feng & Ankenmann,2003)。由于国外学者提出的将概化理论与项目反应理论融合的模型及方法仅仅包含某一二种研究设计，显得比较单一，不能满足概化理论与项目反应理论研究设计的要求。另外，大多数将概化理论与项目反应理论相融合的研究仅囿于题目侧面，较少考虑评分者侧面，显得不足。实际上，Wilson和Hoskens(2001)评分者捆绑模式以及Verhelst和Verstralen(2001)多个评分IRT等模型，也是概化理论与项目反应理论进行融合时适合考虑的评分者侧面模式。

第四，所使用的估计方法缺乏综合比较。一些学者提出的将概化理论与项目反应理论融合的模型及方法所使用的参数估计方法缺乏综合比较，主要表现在：有些研究基于极大似然估计法(Maximum Likelihood Estimation，ML)；有些研究基于限制极大似然估计法(Restricted Maximum Likelihood Estimation，REML)；有些研究则基于期望最大法(Expectation Maximization，EM)；还有些研究则基于MCMC方法(Briggs & Wilson,2007;Li,2009)。Kolen和Harris(1987)使用极大似然估计法给出了一套兼容GT和IRT的方差分量以及人和项目参数估计方法。Patz,Junker，Johnson和Mariano(2002)则使用了限制极大似然估计法和EM算法同时估计概化理论与项目反应理论融合模型HRM的被试能力。由此看来，大多数研究仅仅使用某一二种方法来估计模型参数，缺乏同时用多种估计方法估计模型参数，也缺乏对多种估计方法的性能进行综合比较。例如，ML、REML、EM和MCMC四种方法，可以同时估计模型参数，到底哪种方法更加适合概化理论与项目反应理论的融合模型？是应该基于不同情况不同方法进行综合比较和探讨的。

第五，所输出结果的性能指标难以比较。国外学者提出的将概化理论与项目反应理论融合的模型及方法所输出结果的性能指标难以比较，主要表现在：有些研究仅给出了方差分量估计(Kolen & Harris,1987)；有些研究仅给出了被试能力估计(Patz,Junker,Johnson,& Mariano,2002)；还有些研究则仅给出了概化系数估计(Li,2009)。鲜有研究同时给出方差分量估计、被试能力估计和概化系数估计等三种性能指标。例如，Kolen和Harris(1987)的MM方法输出结果只能提供了方差分量估计，不能提供被试能力和概化系数估计，输出的结果指标有限。Patz,Junker，Johnson和Mariano(2002)提出的HRM方法输出结果仅能够估算被试能力，但不能估算方差分量和概化系数等指标，输出的结果指标也较为有限。Li(2009)仅给出了方差分量估计和概化系数估计，却没有给出被试能力估计等输出结果，输出的结果指标有限。由此看来，大多数研究仅仅给出一二种输出结果指标，显得不够全面。

6 结 语

将概化理论与项目反应理论相融合，可以深化概化理论和项目反应理论研究，为两种现代测量理论走向大统一提供了重要的方法指导，也可以为概化理论和项目反应理论融合后产生新模型进行后续方法研究提供基本保障。目前，有学者初步提出广义项目反应下的概化模型(Generalized Generalizability in Item Response Modeling)的基本思路(Choi,2013)，这种模型既结合了概化理论与项目反应理论的优势，也考虑了MM、HRM、GIRM、GIRMT等模型的特点，在数据分布(数据类型)、研究设计、数学模型、估计方法和输出结果上考虑得更加全面。融合概化理论和项目反应理论是现代测量理论发展的趋势，也将成为当前心理测量学研究的热点。