以不变应万变
2018-12-10 10:09:46
小学生学习指导(高年级) 2018年11期
在百分数应用题中,常会遇到两个或两个以上的变量,但它们的变化过程中,总有一个始终不变的量。如有的题目中的总量是变量,其中的某一部分量是不变量。有的题目中部分量是变量,而总量却是不变的。也有的题目中部分量和总量都发生了变化,但部分量在变化过程中相差数是始终不变的。
例1 商店里有白糖和红糖共630千克,其中红糖占20%,后来又运进一批红糖,这时红糖占白糖总重量的30%,问运进红糖多少千克?
分析与解:这道题中红糖数量发生了变化,但白糖的重量始终没有变,它是一个固定的量,因此,白糖原来的重量为630×(1-20%)=504(千克)。由于运进红糖后,红糖是白糖的30%,所以运进后红糖的总重量是504×30%=151.2(千克),则运进红糖的重量为151.2-630×20%=25.2(千克)。
答:运进红糖25.2千克。
例2 甲、乙、丙三人参加晨练,甲每天跑3000米,乙每天跑的是甲的80%,丙每天跑的是甲的,问乙、丙两人每天跑的路程相差多少米?
分析与解:乙和丙都和甲有关联,甲是一个固定量,乙每天跑3000×80%,丙每天跑,因此,求乙、丙两人每天跑的路程差是
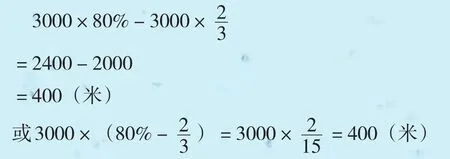
答:乙、丙两人每天跑的路程相差400米。
分数、百分数问题尽管千变万化,但总会找到不变的量,这个不变的量往往就是解题的突破口,只要同学们善于寻找这个不变量,用它来沟通部分量、分率、单位“1”的关系,就能达到顺利解题的目的。
猜你喜欢
娃娃乐园·综合智能(2022年3期)2022-04-19 12:57:08
中学生数理化·七年级数学人教版(2022年3期)2022-03-16 05:55:44
科普童话·百科探秘(2021年12期)2021-01-19 09:16:17
数学小灵通·3-4年级(2020年6期)2020-06-24 06:17:32
小学生学习指导(高年级)(2019年12期)2019-11-13 09:23:04
小学生学习指导(高年级)(2019年6期)2019-01-11 00:19:08
发明与创新·小学生(2018年12期)2018-12-29 09:05:34
新青年(2018年9期)2018-09-14 03:14:58
凤凰资讯报(2016年5期)2016-05-30 10:48:04
恋爱婚姻家庭·青春(2016年4期)2016-04-07 20:54:52

