阴影部分面积是多少

例1 图1是由两个边长相等的正方形组成的长方形，长方形长为10分米，宽为5分米，A是BE的中点，求阴影部分面积。

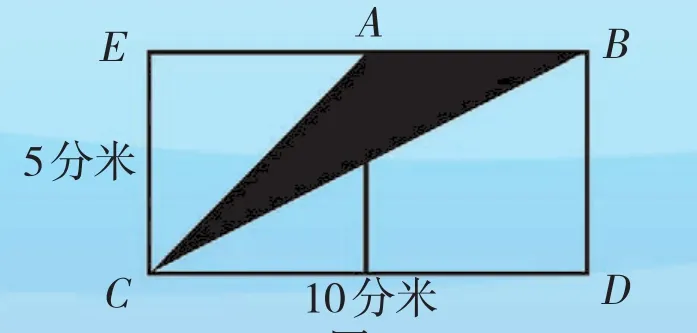
图1

分析与解：求阴影部分面积，就是用总面积减去空白部分的面积。总面积是长方形面积，空白部分的面积就是两个直角三角形的面积和，即△AEC的面积+△BDC的面积。

解法二：长方形的面积：10×5＝50（平方分米）

△AEC的面积＝5×5÷2＝12.5（平方分米）

△BDC的面积＝10×5÷2=25（平方分米）

阴影部分面积＝50－12.5－25＝12.5（平方分米）

答：阴影部分面积是12.5平方分米。

解法二：阴影部分是一个三角形，这个三角形的底是5分米，高是长方形的宽也是5分米。

阴影部分面积=5×5÷2＝12.5（平方分米）

答：阴影部分面积是12.5平方分米。

例2 如图2，已知平行四边形ABCD的面积是90平方厘米，AE是6厘米，CE是10厘米，求阴影部分的面积。

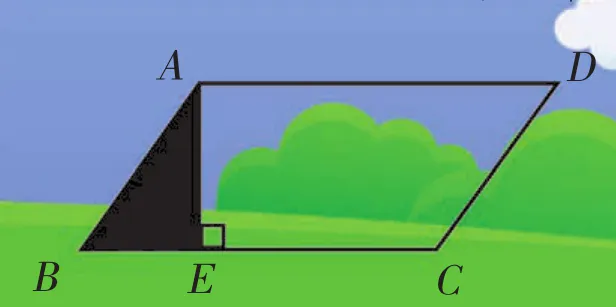
图2

解法一：阴影部分是一个直角三角形，它的高是6厘米，要求它的面积，必须知道BE的长度。AE既是直角三角形的高又是平形四边形的高，题中告诉了平行四边形的面积是90平方厘米，这样就可求出平行四边形底BC的长度。

平行四边形的底：90÷6＝15（厘米）

直角三角形底BE的长度：15－10=5（厘米）

阴影部分面积：5×6÷2=15（平方厘米）

答：阴影部分面积是15平方厘米。

解法二：阴影部分的面积等于平行四边形的面积减去直角梯形的面积，梯形的上底是15厘米，下底是10厘米。

梯形的面积：（15+10）×6÷2=75（平方厘米）

阴影部分面积为：90－75=15（平方厘米）

答：阴影部分面积是15平方厘米。

解法三：连接A、、CC两两点点，，把把平平行行四四边边形形平平分分成成两两个个面面积积都是 （90÷2） 平方厘米的三角形，如图3。

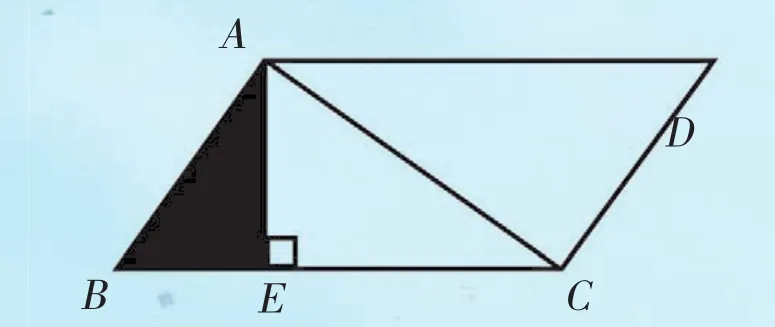
图3

由阴影部分面积=S△ABC－S△AEC，得：90÷2－10×6÷2=45－30＝15（平方厘米）

答：阴影部分面积是15平方厘米。

解法四：过C点作AD边上的高CF，把平行四边形ABCD分成三个部分：长方形AECF和两个相等的直角三角形ABE和和CDF，如图4。

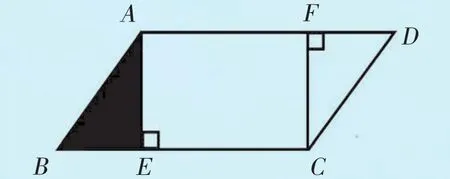
图4

由S△ABE=（S平行四边形－S长方形AECF）÷2，得：（90－10×6）÷2=30÷2＝15（平方厘米）

答：阴影部分面积是15平方厘米。