抗干扰阵列天线的小型化及波束形成技术分析
李 枫,王紫阳,王 乐,李 蕊,冯 罡,尹应增
(西安电子科技大学 天线与微波技术重点实验室,陕西 西安 710071)
随着无线通信的飞速发展,电磁环境也越加复杂,无线通信系统经常受到其他系统的干扰而导致其性能大幅下降,因此抗干扰技术的研究具有非常重要的意义[1-2].
设计抗干扰阵列天线时,一般都是通过减小阵列天线单元之间的间距来实现阵列天线的小型化的[3].随着阵元间距减小,阵元间的互耦会逐渐变强,对阵列方向图的波束零陷产生影响,其精度、深度都会发生改变.笔者针对这个问题开展研究.文献[4]设计了中心频率在 1.268 GHz ,阵元间距为0.5λ(120 mm) 的四元抗干扰阵列天线,把孤立单元的方向图作为阵列方向图的单元因子,根据传统的阵因子理论,从阵列方向图反推阵因子,然后根据阵列排布方式推算出阵元相位加权因子,代入到高频结构仿真(High Frequency Structure Simulation,HFSS)中仿真,阵列方向图在(45°,145°)和(45°,220°)干扰方向上形成的方向略有偏差,零深在 -25 dB 左右的零陷.文献[5]设计了北斗B3频段的四元抗干扰天线阵,其阵元间距为0.5λ(120 mm),根据传统的阵因子理论和自适应零陷算法来形成方向图零陷,其假定干扰方向为 (-20°,45°),结果使得阵列方向图在θ= -21° 方向上形成 -19 dB 的零陷.文献[6]设计了中心频率在 1.575 GHz,阵元间距为0.47λ(90 mm) 的五元全球定位系统(Global Position System,GPS)阵,根据阵因子理论和阵列布局推导出阵元相位加权因子,代入到高频仿真软件HFSS中进行仿真,阵列方向图在干扰方向(45°,30°)上形成了 -36 dB 的零陷.上述文献中的波束形成方法都是基于阵因子理论,天线阵列的阵元间距设计在0.5λ左右,没有考虑阵元间的互耦效应.
笔者针对抗干扰阵列天线的小型化及其波束形成技术开展研究,利用数值分析软件Matlab和高频仿真软件HFSS的联合仿真来进行分析与设计.文中通过减小阵列天线单元之间的间距实现了阵列天线的小型化.从天线阵列单元间的互耦效应出发,对阵列单元的有源阻抗和有源方向图进行了理论分析; 通过天线阵列设计实例研究了互耦对阵元的有源驻波和轴比的影响;利用仿真实例研究了互耦对阵列方向图波束形成的影响.相对于阵因子理论,文中采用有源方向图叠加来计算阵列总场,通过Matlab调用HFSS进行全波仿真分析,利用差分进化算法优化设计,得出最优的阵元加权因子,实现抗干扰阵列天线的波束零陷.研究结果表明,文中提出的设计方法能够非常精准地在干扰方向上形成零陷,并具有较深的零值深度.在多个干扰方向上进行了仿真对比分析,验证了该设计方法的可靠性和准确性.
1 基本理论分析
互耦效应是阵列天线固有的特性之一,是设计阵列和分析误差的重要因素.互耦不仅影响天线阵列的增益和波瓣宽度等电参数,还会使阵列信号的相位和幅度发生改变[7-8].文中通过减小阵列天线单元之间的间距来实现阵列天线的小型化设计,然而随着阵元间距的减小,阵元间的互耦会逐渐变强,阵列的输入阻抗和辐射方向图都会随之改变.在抗干扰天线阵列的设计过程中,单元数量直接影响到整个抗干扰天线阵列的抗干扰性能.一般来说,阵元数量越多,抗干扰天线阵列可以抑制更多方向的干扰信号.文中综合考虑成本、阵列尺寸和阵列排布,以四元阵为例来分析互耦对阵元有源阻抗和有源方向图的影响.
1.1 有源阻抗
设计四元抗干扰天线阵时,基于互耦效应,对阵元的有源阻抗匹配进行分析.根据传输线理论[9],4个端口的电压和电流的关系可以表示为如下的矩阵形式:
(1)

(2)
1.2 有源方向图
对于四元抗干扰天线阵列,天线阵的辐射场可以由4个阵元的场强叠加出,即
(3)

采用阵因子理论分析阵列方向图时,不考虑阵元间的互耦效应,利用单元方向图叠加来表示阵列辐射场,即单元因子乘以阵因子.式(3)中天线阵列的辐射场可表示为
(4)
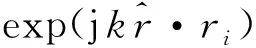
有源方向图是指在天线阵列中,只有1个阵元被激励,而其他3个阵元都接上匹配负载时的辐射方向图[10-12],已考虑了单元间的互耦效应.式(3)的阵列总场可以表示为4个阵元有源方向图的叠加,即
(5)
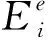
在抗干扰天线阵列的小型化设计过程中,阵元间互耦随着阵元间距的减小而变强,相对于孤立单元的方向图,阵中单元的方向图最大方向会发生偏移.采用阵因子理论的方法来进行波束形成时,阵列总场的计算不计入阵元间互耦,方向图零陷位置会偏移,零陷的深度也会发生改变,影响了抗干扰的性能.而文中的阵列分析方法是利用有源方向图叠加,已计入阵元间互耦效应,能够准确地计算天线阵的阵列总场,形成的方向图零陷位置更精确、零值更深,可以提高阵列的抗干扰性能.
2 天线阵列的小型化设计和仿真分析
2.1 天线阵列的小型化设计
文中设计了一个右旋圆极化微带贴片天线单元,中心频率为 1.268 GHz,采用单点馈电的方式,馈电探针的半径r1= 0.5 mm.方形辐射贴片位于介质基板的上表面,基板选用εr= 10.2,厚度h= 3 mm,损耗角正切是 0.003 5 的正方形介质,尺寸为 55 mm× 55 mm.在介质基板里面加载了3根相同的短路针,短路针到介质基板中心的距离相等,长度h1= 3 mm,半径r2= 0.5 mm.介质基板下表面是尺寸为 70 mm× 70 mm 的地板.微调后天线单元模型的其他尺寸如表1所示.

表1 单元模型参数mm
表1中,L是贴片边长,L1、W1、L2和W2是贴片边缘的小矩形尺寸,fx和fy是相对于贴片中心的馈电位置,d是短路针到介质基板中心的距离.天线单元的结构模型如图1所示.

图1 单元结构示意图图2 阵列结构示意图
设计四元抗干扰天线阵列时,一般都选用0.5λ(120 mm)的阵元间距,而文中将阵元间距缩小为0.375λ(90 mm),实现了阵列天线的小型化设计.阵列布局采用4个单元共地板的结构,其结构模型如图2所示.
2.2 仿真分析
针对上述设计的四元抗干扰阵列天线,为研究阵元间互耦以及4个阵元性能的一致性,对4个阵元的有源驻波和轴比进行了分析,如图3和图4所示.以阵元1为例,又对孤立单元和阵中单元进行了仿真对比分析,研究了互耦对阵中单元有源阻抗和有源方向图的影响,如图5和图6所示.
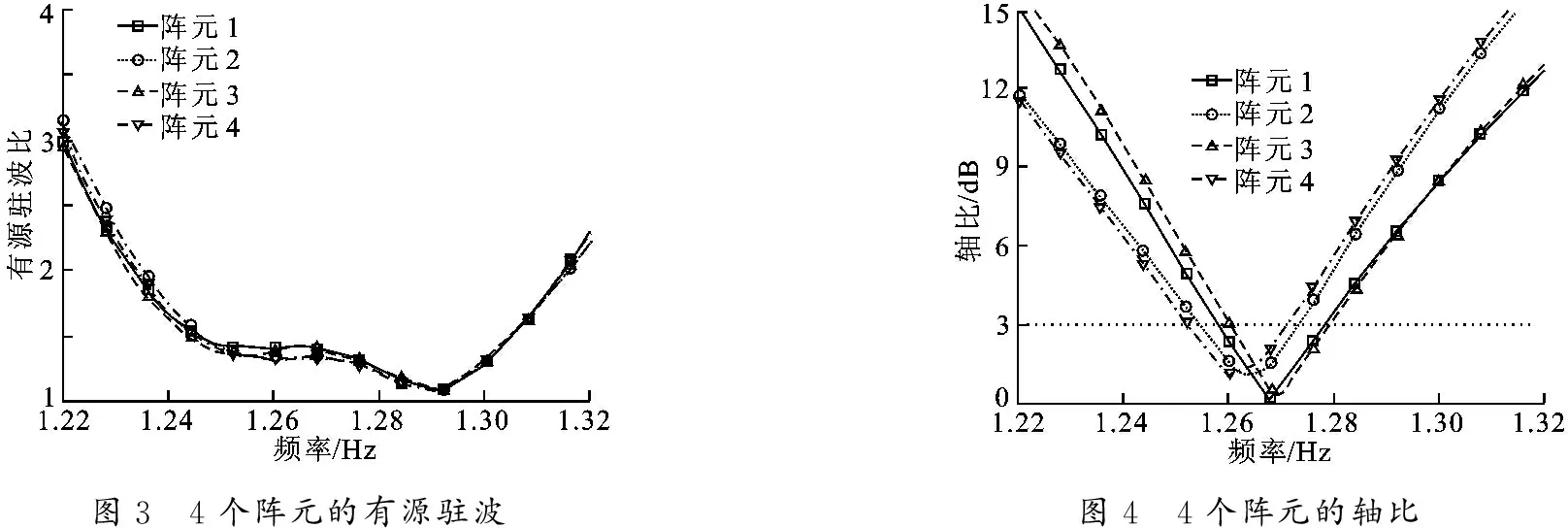
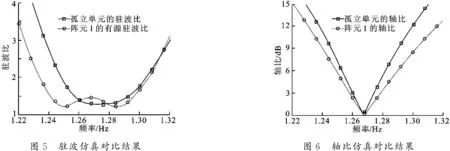
由图3可知,4个阵元的有源驻波曲线基本一致.由图4可知,由于互耦的影响,相邻阵元的轴比曲线产生偏移,而不相邻阵元的轴比曲线基本一致.
由图5可知,孤立单元的驻波带宽为 56.3 MHz,阵中单元1的有源驻波带宽为 81.3 MHz,相对提高了44.4%.由图6可知,孤立单元的轴比带宽为 14.1 MHz,阵中单元1的轴比带宽为 20.1 MHz,相对提高了约42.6%.仿真结果表明,在文中设计的四元抗干扰天线阵列中,阵元间互耦效应对阵中单元的有源阻抗和有源方向图产生了很大影响,使阵中单元的有源驻波和轴比获得了更大的带宽.
3 波束形成技术
文中设计从阵列分析方法和优化方法入手,一方面利用多目标多参数非线性的智能优化算法——差分进化算法[13-14],另一方面采用更加精确的阵列天线数值分析方法——有源方向图叠加.在设计中,天线阵列总场的计算需要对阵列天线进行很多重复工作,还需要利用差分进化算法来优化仿真数据,而HFSS本身不具备该功能.因此,文中提出了Matlab和HFSS联合仿真的设计思路: 编制HFSS VBScript脚本程序来提取阵元的有源方向图数据; 在Matlab中编写基于差分进化算法的优化计算程序; 利用Matlab调用HFSS进行全波仿真分析,得出最优的相位加权因子; 在HFSS进行有源方向图叠加来形成方向图零陷.
假定干扰方向为(30°,10°)(θ=30°,φ=10°),文中设计的主要过程分为如下3步:
(1) 在HFSS中提取4个阵元的有源方向图数据,以提取阵中单元1的有源方向图数据为例,首先提取阵中单元1在φ= 10°方向上辐射电场的两个分量Eθ1和Eφ1,两个分量分别用其实部、虚部合成表示,所以阵中单元1需要提取4组数据: Re(Eθ1)、Im(Eθ1)、Re(Eφ1)和Im(Eφ1).上述工作都是通过编制HFSS VBScript脚本程序实现的.阵列的辐射总场E(θ,φ)可以表示为
其中,Ei(θ,φ)(i=1,2,3,4)为第i个阵元的辐射场,αi为第i个阵元的相位加权因子.
(2) 在Matlab中编写了基于差分进化算法的优化计算程序,对最优的相位加权因子αi进行搜索,使得四元抗干扰阵列天线的方向图在(30°,10°)方向上形成期望的零陷.其中优化算法中目标函数的设计思路为
fitness=U(F0(θ)-Fd(θ)) [b|N-D|] ,
(10)
其中,F0(θ)和Fd(θ)分别是优化得到的当前方向图和期望方向图,N是当前零陷的零值深度,D是与N相对应的期望值,b为加权系数.
(3) 在HFSS中,将最优相位加权因子αi代入阵元i的激励相位,通过阵列方向图的仿真来验证文中设计方法的正确性.
对两种波束形成方法进行仿真对比分析,当干扰方向为(30°,10°)时,采用阵因子理论的仿真结果如图7所示,采用文中设计的仿真结果如图8所示.
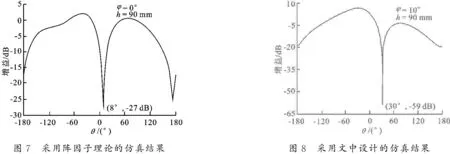
从图7可以看出,干扰方向为(30°,10°)时,采用阵因子理论的仿真结果中,阵列方向图零陷方向为(8°,10°),偏移了22°,零陷深度也只有 -27 dB.从图8可以看出,干扰方向为(30°,10°)时,采用文中设计的仿真结果中,阵列方向图能准确地在其干扰方向上形成零陷,零深能达到 -59 dB.
表2给出了针对不同的干扰方向,采用阵因子理论的仿真结果.表3给出了针对不同的干扰方向,采用文中设计的仿真结果.

表2 采用阵因子理论的仿真结果

表3 采用文中设计的仿真结果
从表2可以看出,当干扰方向为(60°,10°)时,采用阵因子理论的仿真结果中,阵列方向图零陷方向为(31°,10°),偏移了29°,零深只有 -17 dB.在其他几个干扰方向的仿真结果中,阵列方向图零陷方向都发生了偏移,零陷深度也都较浅.从表3可以看出,采用文中设计的仿真结果中,阵列方向图都能准确地在其干扰方向上形成零陷,零深也相对较深.例如,在(20°,10°)方向上形成 -55 dB 的零深,在(60°,10°)方向上形成 -60 dB 的零深.
仿真结果表明,文中设计的四元抗干扰天线阵列,由于阵元间的互耦效应,阵因子理论的方法在其波束形成过程中已不可靠,而文中提出的联合仿真的设计方法能够非常精准地在干扰方向上形成零陷,并具有较深的零值深度.由于计入互耦效应,该设计方法可以适用于任意阵元间距、任意阵列结构的抗干扰天线阵列.
4 结 束 语
文中基于四元抗干扰天线阵的互耦效应,对阵元的有源阻抗和有源方向图进行了理论分析.通过减小阵列天线单元之间的间距实现了阵列天线的小型化设计,并研究了互耦对阵元的有源驻波和轴比的影响.通过Matlab调用HFSS进行全波仿真分析,利用差分进化算法优化设计,得出最优的阵元加权因子来实现阵列天线的波束零陷,并从仿真实例上分析了互耦对阵列方向图波束零陷的影响.结果表明,文中提出的设计方法能够非常精准地在干扰方向上形成零陷,提高了方向图零陷的精度和深度,改善了抗干扰天线阵列的波束形成.文中的研究为抗干扰阵列波束形成提供了很好的设计方法,并通过设计实例验证了其正确性,对抗干扰阵列天线的设计提供了保障.

