一种有效的LDPC码伪码字搜索算法
郭军军,白硕栋,慕建君,荆 心,肖 锋
(1. 西安工业大学 计算机学院, 陕西 西安 710021;2. 西安电子科技大学 计算机学院,陕西 西安 710071)
低密度奇偶校验(Low-Density Parity-Check, LDPC)码是文献[1]在1962年提出的一种现代纠错编码技术.因具有简单的编译码方法和可逼近香农容量限的译码性能,LDPC码已经成为当今工业界和学术界的研究热点之一.但是,当采用消息传递迭代译码算法时,LDPC码在高信噪比区域存在错误平台现象.而低重量伪码字(Pseudo-codeword)是造成LDPC码译码错误平台问题的主要原因之一.因此,研究LDPC码低重量伪码字的有效搜索方法是评估和改进其译码性能的关键.
搜索LDPC码的伪码字是一个非确定多项式(Non-deterministic Polynomial,NP)难问题[2].国内外目前关于这方面的研究方法可概括为两大类:Tanner子图枚举法.根据Tanner图结构来搜索停止集(Stopping Set)和陷阱集(Trapping Set)等有害子图,从而确定LDPC码的伪码字.由于规则LDPC码的陷阱集是由短环以及与短环相连的路径组成的[3],文献[4]中提出了基于短环的路径扩展法可以有效地找出陷阱集,再通过偏置陷阱集噪声来搜索规则LDPC码线性规划译码的伪码字. 文献[5]提出了非规则LDPC码陷阱集的一种穷举搜索方法. 该方法的基本思路是首先从Tanner图中找出一个短环或度数较小的变量节点作为基础,然后通过单边、路径或棒棒糖(lollipop)子图方式进行扩展来找到非规则LDPC码消息传递译码的陷阱集,从而确定对应的伪码字[5].但是,这类伪码字搜索算法属于一种穷举算法,随着码长和陷阱集尺寸增大,其效率变得越来越差.随机噪声输入验证法.该类方法首先产生随机噪声输入向量,然后经多轮迭代促使译码器译码失败而产生伪码字. 文献[6]提出的基于快平直方图(Fast Flat Histogram,FFH)的搜索方法可以有效地找到加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道下置信传播(Belief Propagation,BP)译码时LDPC码的伪码字[6].通过构造随机信道噪声,文献[7-8]中提出的瞬子搜索算法(Instanton Search Algorithm,ISA)可在有限次迭代后找到LDPC码线性规划伪码字.然而,译码器输入的随机性导致这类伪码字搜索方法的效率较低.
针对上述方法的不足,笔者提出了针对二元对称信道(Binary Symmetric Channel, BSC)下LDPC码的一种线性规划译码的伪码字搜索算法.仿真实验结果表明,与现有伪码字搜索算法相比,所提算法能够更准确地找到中短码长规则和非规则LDPC码的低重量伪码字.
1 相关术语及定义
令G=(V∪C,E)是LDPC码Θ的Tanner图.Tanner图G是一种特殊的二部图,其顶点是由变量节点和校验节点组成的,变量节点集V= {v1,v2,…,vn},校验节点集C= {c1,c2,…,cm},n和m分别表示变量节点数和校验节点数,E是校验节点与变量节点之间相连的边集,即E= {v,c:v∈V,c∈C}.与变量节点v相连的校验节点集记作N(v)= {c:c∈C,v,c∈E},相应地,与校验节点c相连的邻居变量集记为N(c)= {v:v∈V,v,c∈E}.由于LDPC码的校验矩阵具有稀疏性特点,故图G的边数较少.若码Θ的Tanner图中所有变量节点和校验节点的度分布相同,则称该码为规则LDPC码;否则,称之为非规则LDPC码.
定义1 实数集上的向量u的支持集fsupp(u)定义为u的非零分量的位置下标集合[7],即fsupp(u)= {i:ui∈u}.
定义2 二元LDPC码校验多胞体(Check Polytope)定义为所有长度为d的校验行组合向量构成的凸包,并且每个行向量x中有偶数个1,即Pd=fconv({x∈ {0,1}d|x中含有偶数个1})[9].
定义3 设一个LDPC码Θ的校验矩阵为H,则线性规划译码时Θ的伪码字p定义为H所对应的松弛校验多胞体上的非整数顶点.
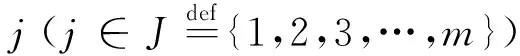
(1)
在式(1)中,其增广拉格朗日函数为
(2)
其中,yj为拉格朗日乘子;υ>0,为惩罚参数.在ADMM迭代处理中,x、z和y的更新规则为
其中,函数ΠPdj(v)表示向量v在校验多胞体Pdj上的欧几里德投影.

(6)
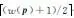
2 伪码字搜索算法
2.1 算法的提出
在二元对称信道下,LDPC码线性规划译码失败时输出为非整数伪码字.而低重量伪码字是造成错误平台现象的最直接原因之一.通过大量观察分析可知,有害的Tanner子图中变量节点的位置恰好与伪码字向量中非整数位置重合.对于规则LDPC码,这些伪码字仅仅与Tanner图中短环结构有关,而对于非规则LDPC码,伪码字还与Tanner子图中含有度数较低的变量节点有关.特别地,非规则LDPC码的伪码字与变量节点度数为2的Tanner子图结构密切相关.度数为2的节点可以抑制短环的出现,同时使得码的汉明距离变小,这就降低了译码性能.因此,在搜索非规则LDPC码的低重量伪码字时,应考虑短环和与度数为2的变量节点相关的有害Tanner子图结构.典型的有害Tanner子图主要包括线性、树状和环形结构三大类,如图1所示.
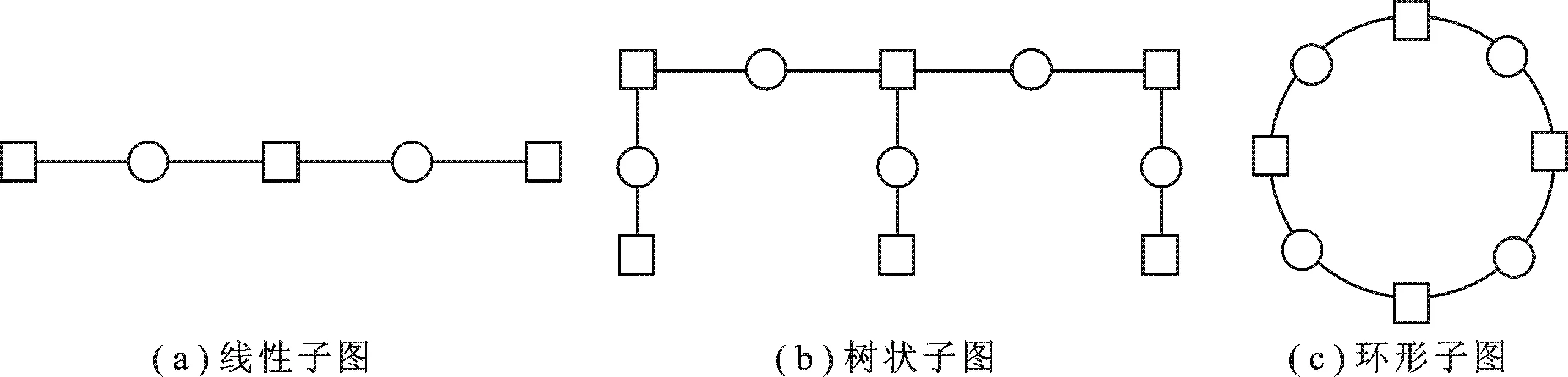
图1 典型的有害Tanner子图结构(○表示变量节点,□表示校验节点)
受到基于Tanner图搜索陷阱集和瞬子搜索算法的启发,文中提出了一个以Tanner子图为基础的低重量伪码字搜索(Low-Weight Pseudo-Codewords Search, LW-PCS)算法.该算法的基本思想是首先枚举有害的Tanner子图结构;其次选择全零码字作为译码器的输入,并叠加随机产生的足够大的信道噪声而导致译码器输出伪码字,确保有害Tanner子图中变量节点对应位置的输入码字存在噪声;最后借助ISA搜索算法,找到该噪声结构对应的所有低重量伪码字.
2.2 算法的描述
设一个LDPC码的有害Tanner子图集为S,相应的伪码字集为P,二元对称信道下LDPC码ADMM线性规划译码时的LW-PCS低重量伪码字搜索算法如下:
(1) 初始化,令P←{Ø}.
(2) 从S中取出一个Tanner子图s,并构造s中变量节点集合V.
(3) 对于全零向量r,随机产生不少于|V|个扰动噪声来翻转r中对应位置的比特信息,并确保r中对应集合V的所有分量的比特值为1,从而得到向量r′.
(4) 令k←1,并对输入向量r′进行ADMM线性规划译码得到输出伪码字pk.
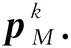


(8) 对于任意it∈fsupp(M(pk))(1≤t≤|fsupp(M(pk))|),令rit是一个具有fsupp(M(pk))it支持集的向量,pit为不同的rit进行ADMM线性规划译码后得到的伪码字向量.
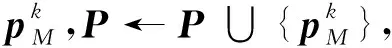
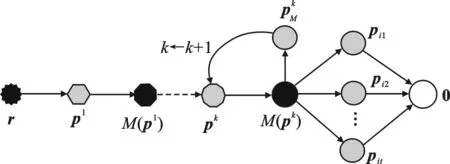
图2 输入向量r的ADMM线性规划译码伪码字收敛过程
LW-PCS算法中符号|V|表示集合V的分量的个数.在步骤(2)中,构造包含度为2的变量节点Tanner子图时节点的数量应不少于分数距离的一半; 步骤(3)中增加过多扰动随机噪声会影响译码算法的收敛速度,因此,扰动噪声的数目通常不超过码长的 1/2.
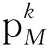
3 仿真实验及分析
为验证文中所提出伪码字搜索算法的准确性,选择了一个典型的规则Tanner码[11]和一个非规则的PEG码进行数值仿真.
例1 (155,64)Tanner码.Tanner码是一个码长为155的规则LDPC码.该码的校验行数为93,分数距离为 8.349 8.Tanner码的伪码字最低重量wmin≈ 16.404.首先,采用文献[12]方法找出长度为8、12、14和16的所有短环,然后利用文中提出的算法搜索伪码字时,仅经过 3 700 次的尝试即可得到155个低重量伪码字.然而,利用现有的ISA搜索算法必须进行 112 320 次搜索尝试才能够找到这155个低重量伪码字(如表1所示).

表1 两种伪码字搜索算法伪码字搜索次数比较
例2 PEG构造的非规则LDPC码.本实验中选择了一个PEG算法构造的码长为504的PEGirReg 252× 504码.该码中变量节点度为2的节点约占全部变量节点的32%.由于PEGirReg252×504码是非规则LDPC码,因此笔者在构造LW-PCS算法的输入集时,充分考虑了含有短环的Tanner子图以及度为2的变量节点所构成的子图结构对伪码字搜索算法的影响.采用LW-PCS算法需要 598 289 次搜索即可找到该码的291个低重量伪码字.但是,采用现有的ISA搜索算法必须进行106次尝试才仅仅能够找到232个低重量伪码字,如表1所示.
由此可见,与传统的ISA搜索算法相比较,文中提出的LW-PCS搜索算法能够通过较少的尝试次数即可快速准确地找到LDPC码的主要低重量伪码字.
4 结 束 语
笔者针对二元对称信道下LDPC码线性规划译码,提出了一种基于Tanner子图知识的低重量伪码字搜索算法.仿真结果表明,与现有伪码字搜索算法相比,所提出的LW-PCS搜索算法能够准确地找出中短长度的规则和非规则LDPC码的伪码字.虽然笔者提出的搜索算法可以找到许多低重量伪码字,但并不能保证该算法能够找到全部低重量伪码字.因此,如何设计更加高效的伪码字搜索算法有待于进一步研究.

