预编码增益优化的预编码叠加训练设计

王青波，窦高奇，高 俊

(海军工程大学 电子工程学院，武汉 湖北 430033)

叠加训练方案将训练序列与数据序列叠加，以消耗部分发射功率为代价实现信道估计，不需消耗额外的频带资源[1]．相较于时分、频分方案节省了训练序列占用的带宽资源，有效提高了频谱效率．但在叠加训练方案中，数据信息对信道估计造成干扰，导致信道估计性能较弱，符号检测性能较差[2]．预编码叠加训练方案通过预编码映射将数据与训练序列映射到不同正交子空间传输，从而消除数据传输对于信道估计的干扰．现有的预编码叠加训练方案可按预编码矩阵类型分为秩亏预编码叠加训练与满秩预编码叠加训练两类[3]．秩亏预编码叠加训练(如数据依赖的叠加训练(Data Dependent Superimposed Training，DDST)[4])方案采用秩亏矩阵作为预编码矩阵，通过预编码在发送端引入数据失真为代价实现数据训练正交传输．然而，当采用高阶调制或信道阶数较大时，随着预编码提升信道估计性能的同时增大了数据失真，导致符号检测性能下降[4-5]．针对此问题，满秩预编码叠加训练(如多相序列预编码叠加训练(Polyphase sequence-based Precoding Superimposed Training，PPST)[5])方案采用满秩矩阵作为预编码矩阵，在实现数据训练序列正交传输的同时，不引入数据失真，在高阶调制或信道阶数较大时，仍保持较好的符号检测性能[3， 5]．

预编码叠加训练方案的优化设计主要包括预编码矩阵与训练序列的优化设计．其中秩亏与满秩预编码叠加训练方案中的训练序列的优化设计问题，均已从优化信道估计性能为目标解决[6-7]．秩亏预编码叠加训练方案中，由于预编码引入的数据失真导致符号检测性能下降，以最小化数据失真为目标的预编码优化设计已被提出[3]．然而，满秩预编码叠加训练模型中预编码优化设计问题仍有待研究．结合编码理论，当预编码矩阵采用满秩矩阵时，在消除数据传输对信道干扰的同时会提供额外的预编码增益．如文献[8]中提出的线性预编码正交频分复用系统(Linear Precoding Orthogonal Frequency Division Multiplexing system， LPOFDM)通过预编码将数据信息扩展到更宽频带范围获取满频率分集，以提高符号检测性能．文献[9]采用预编码的方法实现了双中继协作网络的满分集性能．文献[10]提出采用带预编码的空时编码获取多输入多输出系统的满频率与空域分集性能．文献[11]基于广义特征值分解设计预编码与解码矩阵，获取到多小区多输入多输出系统的更高自由度．

笔者针对满秩预编码叠加训练方案，在保证获取与现有方案相同信道估计性能的同时，以优化预编码增益，提高符号检测性能为目的．借助成对错误概率(Pair-wise Error Probality，PEP)分析，推导满秩预编码叠加训练模型中预编码带来的分集和编码增益，导出相应的优化策略，并据此提出采用一组满足特定自相关、互相关特性的线性调频(Chirp)序列构成预编码矩阵与训练序列，构建基于Chirp序列的预编码叠加训练(Chirp sequence-based Precoding Superimposed Training，CPST)方案．理论分析表明，采用Chirp序列较现有方案采用变换域多相序列[5]获取更优的编码增益．仿真结果表明，文中方案在高信噪比环境下能有效提高符号检测性能．

1 满秩预编码叠加训练模型

考虑单载波块传输系统，信道为准静态瑞利多径信道，信道信息在数据块内不发生变化，在块间可以发生变化，并在数据块前插入循环前缀消除块间干扰．使用s表示Ns×1 维数据序列，P表示N×Ns维满秩预编码矩阵 (N>Ns)，并满足能量约束条件 tr{PHP}=Ns，c表示N×1 维训练序列．则在接收端去除循环前缀后的接收信号可表示为

y=H(Ps+c)+v，

(1)

CPi=0，i=1，…，Ns．

(2)

(3)

其中，CHC为正定矩阵，根据tr{(CHC)-1}≥L2/tr{CHC}，等式成立的约束条件[3， 5]为

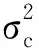
(4)

2 成对错误概率分析

2.1 PEP推导

推导满秩预编码叠加训练模型准确的符号错误概率闭合表达式难度较大，难以实现．文中借助PEP进行错误概率一致界分析，推导满秩预编码带来的分集和编码增益，以及获取满分集增益与编码增益优化的约束条件．

(5)

(6)

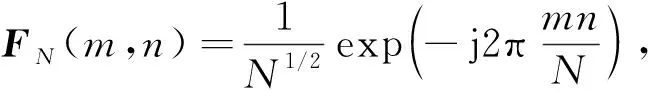
(7)

2.2 分集、编码增益分析

分集阶数d可表示如下:

(9)

因FL为L阶满秩矩阵，故欲获取满分集增益d=L，则预编码矩阵必须满足如下约束条件:

(10)

因此，获取满分集增益，等价于要求预编码矩阵P的每一列在频域至少有L个非零频点．

若将正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)看作预编码矩阵为傅里叶变换矩阵FN的特例，FN的每一列在频域表现为一个非零频点，则获取分集性能为1．因此，可采用LPOFDM将频域信号扩展到更宽带宽范围内获取满分集增益，提高符号检测性能．

现对编码增益进行分析，根据式(8)，预编码矩阵应使得det(Θ)最大化．因Θ与符号错误数量、位置及调制方式相关，欲遍历分析det(Θ)的优化设计难以实现．因发送数据各符号被映射到预编码矩阵各列传输实现正交传输，在信道均衡后可以近似认为各符号独立传输．因此，文中推导具有较强指导意义的错误符号数为1，错误位置任意时的det(Θ)优化条件，并对不同调制方式进行能量归一化处理，故在下述分析过程中，不再考虑信号能量．

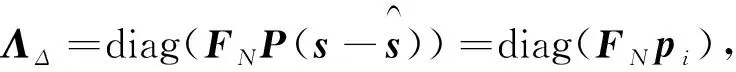
(11)

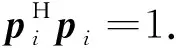
∀i∈1，2,…，Ns．

(12)

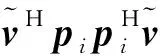
(13)

由约束条件(13)可知，实现符号s(i)的PEP最大值最小化等价于要求预编码矩阵的任意列pi在频域表现为N个非零等幅频点．

3 基于Chirp序列的预编码叠加训练方案

3.1 CPST方案设计

为实现更优的预编码增益，文中提出采用一组满足特定自相关与互相关特性的Chirp序列构建预编码叠加训练模型，该组Chirp序列在文献[12]中用于构建菲涅耳变换的一组正交基，可将数据序列的各个符号能量均匀扩展到相同带宽的频域范围内．故采用此Chirp信号构建预编码矩阵时，预编码矩阵的各列在频域均表现为间隔为零的等幅频点，在获取满分集增益的同时，获取更优的编码增益．

首先给出该组Chirp序列的数学模型如下:

(14)

下面给出此组信号的相关性约束条件，Φ(:，ni)表示Φ的第ni列，Φ(:，ni)k表示Φ的第ni列向下循环移k位后的序列，以下相关性证明在N为偶数的假设下进行(N为奇数时，可类似证明)．

当np=nq时，等式(15)给出Φ各列的自相关特性，即各序列与其循环移位序列不相关．

当np≠nq时，等式(15)给出Φ各列的互相关特性，即当满足条件 mod(k+np-nq，N)=0 时，Φ的第np列与第nq列循环移k位后的序列相关；否则，不相关．

根据矩阵Φ各列的自相关和互相关特性，CPST方案构建如下: 选取Φ的任一列作为训练序列，并选择去除训练序列及其前后各L-1 列的N-2L+1 列构成预编码矩阵．如当选用Φ(:，1)构成训练序列c，则选用Φ(:，L:N-L+1)构成预编码矩阵P，此时接收端去除循环前缀后的信号可表示为

y=H(Φ(:，L-1:N-L+1)s+Φ(:，1))+v．

(16)

由相关性条件可知，选取Chirp序列酉矩阵Φ相应列构成的预编码矩阵与训练序列满足约束条件(2)，实现了数据与训练的正交传输，消除了数据对信道估计的干扰．并满足约束条件(4)，实现了信道估计的最小均方误差．因此，文中CPST方案获取与DDST，PPST相同的信道估计性能．

3.2 分集、编码增益对比

下面通过对文中CPST方案与现有的PPST方案进行分析对比，说明文中方案获取更优的预编码增益．

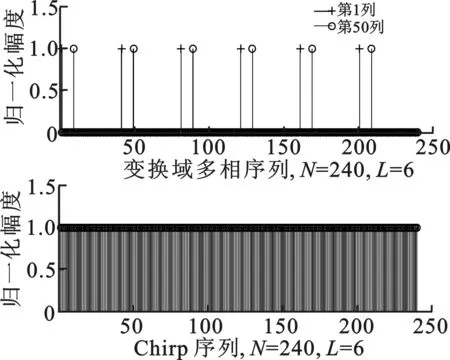
图1 PPST与CPST的预编码矩阵列向量频谱结构

首先对分集增益进行对比，PPST方案中采用的变换域多相序列在频域为均匀分布的L个等幅频点，文中CPST方案的Chirp序列在频域为N个等幅频点，频域结构如图1所示．根据约束条件(10)，PPST方案与文中CPST方案均可获取满分集增益．

其次对编码增益进行对比，当pi为变换域多相序列时，其频域为L个非零等幅点．而当pi为文中的Chirp序列时，其频域为全覆盖的N非零等幅点．根据约束条件式(13)，文中CPST方案较PPST方案获取更优的编码增益．

特别地，PPST方案将每个符号在频域均匀扩展到L不同频点传输，获取了满分集性能，但是由于加性高斯噪声的能量非均匀分布特性，影响接收端各符号解调的噪声能量会因相应L频点噪声的变化而变化，可能导致部分符号的信噪比大大降低，造成符号传输错误．而文中CPST方案将每个符号均匀扩展到全部频点上传输，由约束条件式(12)和式(13)可知，接收端各符号均化了噪声影响．特别在高信噪比环境下，文中CPST方案的噪声均化保持了接收端各符号的高信噪比，而PPST方案会由于高斯噪声能量非均匀分布特性导致部分符号受噪声影响较大，产生传输错误．

图2 信道估计性能比较

因此，文中CPST方案较PPST方案获取更优的编码增益，实现更优的符号检测性能．

4 仿真分析

由图2描绘的MSE曲线可知，瑞利衰落信道阶数为2和6时，文中CPST方案与DDST、PPST方案获取一致的信道估计性能．验证了文中方案训练序列满足约束条件式(4)，获取与现有方案一致信道估计性能的结论．

由图3和图4描绘的SER性能曲线可知，文中CPST方案无论在信道阶数较大 (L=6) 或较小 (L=2)，以及采用高阶调制(十六进制正交幅度调制(16-ary Quadrature Modulation，16QAM))或者低阶调制(四相相移键控(Quadrature Phase Shift Keying，QPSK))时，性能均优于PPST与DDST方案．采用低阶调制时，DDST方案性能优于PPST方案性能．采用高阶调制时，PPST方案性能优于DDST方案性能．且3方案在信道阶数为6时的性能均优于信道阶数为2时的性能．

根据式(11)绘制CPST与PPST方案错误符号数量为1时理论PEP最大值曲线．由于没有遍历所有符号错误数量可能，及在理论PEP推导中的近似放大处理，致使理论PEP曲线与仿真SER曲线之间存在量的差距，但是两者的变化趋势基本一致，说明PEP曲线能较好地体现SER性能的变化．在低信噪比下，符号错误数量为1的概率较低，故出现理论PEP大于仿真SER的情况．

由约束条件式(10)及CPST，PPST方案中预编码矩阵列向量频谱结构图，3方案均获取满分集增益性能，因此，3方案在高信道阶数时性能均优于在低信道阶数时的性能．其次，DDST方案通过发送端预编码，以数据失真为代价实现训练与数据的正交传输．在采用高阶调制时，由于预编码带来的失真较大，致使接收端符号检测性能较弱．而PPST方案不引入数据失真，故在高阶调制时，PPST方案性能优于DDST方案的．在采用低阶调制时，DDST预编码造成的发送端数据失真较小，并将符号扩展到整个传输带宽，而PPST方案虽没有引入数据失真，但是只将每个符号在频域扩展到L个频点传输，由于不满足约束条件式(13)，预编码提供的编码增益较低，因此，DDST方案较PPST方案获取更优的性能．文中提出的CPST方案通过满秩预编码使得训练与数据正交传输，不引入数据失真．且将每个符号均匀扩展到全带宽内传输，满足约束条件式(13)，因此，在获取更优编码增益时，CPST方案在不同信道阶数及调制方式下，其性能均优于PPST与DDST的．

5 总 结

笔者提出基于Chirp序列的预编码叠加训练方案，选用Chirp序列构建预编码矩阵与训练序列，实现数据与训练的正交传输，将各符号均匀扩展到整个传输带宽内，在获取与DDST，PPST相同信道估计性能的同时，优化预编码提供的编码增益．仿真结果表明，文中方案在不同信道阶数及高、低阶调制时均获取更优的符号检测性能．特别在高信噪比环境下，可显著提升符号检测性能．