采用三维偶极线圈的无线电能传输系统多自由度拾取机构

冯天旭, 王智慧, 孙 跃, 唐春森

(重庆大学自动化学院, 重庆市 400044)

0 引言

近年来,利用磁场耦合和谐振实现无线电能传输(WPT)从小功率充电(例如医疗植入设备)到中型或大功率设备(例如电动汽车)得到了广泛的研究和应用[1-4]。目前,Rim等人提出的偶极线圈结构在感应耦合电能传输(ICPT)模式下可以实现5 m传输209 W[5],7 m传输11 W的功率[6],这种偶极线圈结构对于较低频率的感应电能传输系统的中远距离传输提供了一个较好的思路。为了提升无线电能传输系统的灵活性,国内外科研工作者从不同方面做了大量工作,文献[7-11]从改变发射线圈结构以及控制方式上研究,分别用2个和3个正交的环形线圈作为发射线圈,通过控制原边线圈中的电流,使其产生旋转磁场,接收线圈在离发射线圈一定范围内全方位拾取电能。也有文献针对接收线圈结构进行设计,文献[12]采用正四面体线圈作为拾取机构,实现了功率60 W、效率60%的多自由度能量传输。文献[13]采用三维正交环形线圈作为拾取机构实现多自由度全方位传能,其体积小,但是输出功率也很小,工作频率达到100 MHz,由于实验比较困难,其只做了仿真分析。也有文献同时利用多个发射线圈和多个接收线圈来提高电能拾取的自由度,文献[14]采用交叉偶极线圈作为发射和接收线圈,发射机构和拾取机构均为平面型,节约了空间体积。

本文结合了偶极线圈结构可以实现较远距离传输和利用多个接收线圈可提升拾取电能自由度的优势,优化设计了一种面向多自由度应用磁能拾取机构。首先,对三维偶极线圈的磁路进行了分析,从而引出对3个拾取线圈输出组合方式的讨论,选取整流后串联模式搭建了多维偶极线圈等效电路模型,得出系统的等效互感与功率的关系,以系统的输出最大功率及输出平稳性为优化目标,通过配置拾取线圈的匝数,来满足等效互感要求以满足输出要求;然后,利用COMSOL仿真比较了环形线圈和偶极线圈在多自由度能量拾取方面的优劣,得出同等空间体积下偶极线圈比环形线圈功率密度高的结论;最后,设计实验验证该拾取机构可以在距离发射机构上面2 cm处任意旋转下实现输出电压较为稳定且拾取功率维持在10 W以上。

1 三维偶极式拾取机构

1.1 拾取机构模型

本文选取三维十字架磁芯作为拾取机构骨架,该拾取机构由3个两两垂直的偶极线圈Rx1,Rx2,Rx3组成,发射线圈Tx以圆盘形线圈为例,位于拾取机构正下方,耦合机构如图1所示。为保持高度对称性,3个拾取线圈设计的尺寸完全相同,分别绕制在三维十字架磁芯上。

1.2 拾取机构的多自由转动状态

拾取机构的旋转状态见附录A图A1,AB,CD,EF分别表示3个两两正交的偶极拾取线圈

图1 耦合机构示意图Fig.1 Schematic diagram of coupler

Rx1,Rx2,Rx3;A1B1,C1D1,E1F1表示旋转后的拾取线圈。若拾取机构绕X或Y轴旋转,则对应X或Y轴上的拾取线圈的互感一直为零,若拾取机构绕Z轴旋转,则Z轴上的拾取线圈一直保持最大,而X和Y轴上的拾取线圈的互感一直为零。为了使3个拾取线圈的互感都会随着旋转角度变化,因此选取X轴和Y轴角平分线作为转轴,定义拾取机构绕转轴顺时针旋转的角度为θ,每个拾取线圈的长度为2l,则旋转过程中的坐标变化可表示为:

(1)

1.3 磁路分析

当拾取机构在空间中多自由度运动时,空间位置的改变会引起互感的变化从而影响能量传输,原边线圈平行于XY平面,位于拾取机构正下方,其匝数为N1,通入电流为Ip,近似为产生竖直向上且恒定的磁通密度Bt,定义其方向为n=(0,0,1),如图2所示,将发射线圈产生的磁力线正交分解为3个方向[15]:1个垂直于拾取线圈平面Bz,另外2个平行于拾取线圈平面Bx和By,则通过3个拾取线圈的磁链为:

(2)

式中:A为单匝线圈的面积;N2为拾取线圈的匝数。

图2 一个偶极拾取线圈的磁通Fig.2 Magnetic flux of a dipole pick-up coil

由式(1)和式(2)可得:

(3)

每个拾取线圈的感应电动势可表示为:

(4)

每个拾取线圈对于发射线圈的互感Mpi可表示为:

(5)

上式表明每个拾取线圈的感应电动势和互感的大小和方向都随着旋转角度做周期性变化,因此引出对拾取线圈输出组合方式的分析。

2 拾取机构输出方式及系统电路模型

2.1 拾取线圈输出组合方式分析

由于该三维正交偶极拾取线圈在实际应用中需要为一个负载供电,因此需要考虑3个绕组的连接拓扑,根据不同的串并联及整流模式可分为串联后整流、并联后整流、整流后串联及整流后并联4种拓扑,电路模型如附录A图A2所示。

对于该三维偶极拾取线圈,由于各绕组的输出电压不一定相同,若采用并联后整流方式,并联连接的各绕组的内阻电压降较大进而导致电能消耗,为满足基尓霍夫电压定律,输出电压也降低,严重时耦合系数较大的拾取线圈可会被短路解耦[16],因此,不考虑这种方式。拾取机构在做多自由度转动时,由于同名端不同,每个拾取线圈对发射线圈的互感有正有负,若直接将3个拾取线圈串联,拾取机构对发射线圈串联后整流的等效互感Msr可表示为:

(6)

对于整流后并联模式,由于整流二极管的钳位作用,只有互感最大对应的绕组才有输出,因此拾取机构对发射线圈整流后并联的等效互感Mrp可表示为:

Mrp=max{Mp1,Mp2,Mp3}

(7)

对于整流后串联模式,3个拾取线圈在同一个回路之中,所以3个线圈的电流幅值必定相等,相位要么相同,要么相差180°。互感不同则拾取电压不同,同名端的不同会使拾取电压的相位相反,但经过整流之后3个拾取线圈的电压方向相同,因此整流后串联模式可以忽略线圈同名端的问题,拾取机构对发射线圈整流后串联的等效互感Mrs可表示为:

(8)

根据式(6)—式(8),在相同参数条件下画出3种等效互感曲线如图3所示,可知串联后整流模式下等效互感Msr波动较大且会出现抵消的情况,在某些旋转角度下等效互感为零,拾取不到能量;整流后并联模式下等效互感Mrp比较小,线圈利用率低;整流后串联模式的等效互感Mrs较大且波动较为平稳,三维偶极线圈利用率高。综上,本文选取整流后串联模式作为三维偶极式线圈的输出方式。

图3 3种输出模式下的等效互感Fig.3 Equivalent mutual inductance under three output modes

2.2 三维偶极式线圈电能传输系统模型

多自由度拾取电路模型如图4所示,Ud为直流输入电压,U为逆变输出电压有效值,Cp为原边串联谐振补偿电容,Csi为副边第i个偶极线圈的串联谐振补偿电容,Lp为原边线圈的自感,Lsi为副边第i个偶极线圈的自感,Rp为原边线圈内阻,Rsi为副边第i个偶极线圈的内阻,RL为负载电阻。

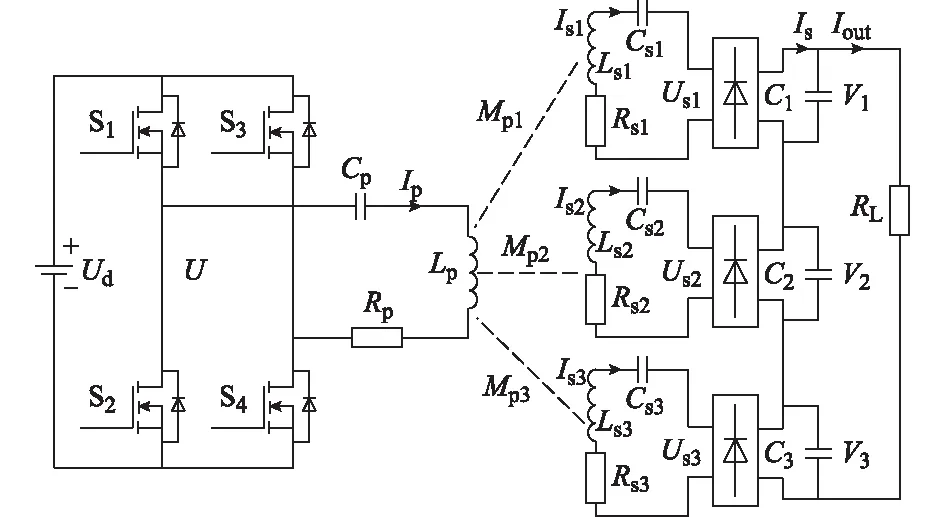
图4 多自由度拾取电路模型Fig.4 Model of multi-degree pick-up circuit

由于整流后串联输出,输出电压Uo为3个拾取电压之和,即

Uo=V1+V2+V3

(9)

V1,V2,V3为整流滤波后的电压,则对应整流前的电压Us1,Us2,Us3可表示为:

(10)

由于3个偶极拾取线圈两两正交,因此可忽略拾取线圈两两之间的互感,当系统工作在谐振状态时,由互感耦合理论可得[17]:

(11)

式中：ω=2πf，其中f为系统的工作频率。

由于整流后串联连接,因此Is=Is1=Is2=Is3,拾取机构与发射线圈的等效互感M=|Mp1|+|Mp2|+|Mp3|,忽略整流桥内阻,定义3个拾取线圈的串联内阻Rs=Rs1+Rs2+Rs3,由式(9)—式(11)可得:

(12)

则负载电流为:

(13)

系统的输入、输出功率分别为:

(14)

系统的输出效率为:

(15)

3 耦合机构优化设计

3.1 系统输出特性分析

互感是影响功率和效率的关键参数,根据式(14)和式(15)来分析互感对系统的能效特性的影响,令dPout/dM=0,可得:

(16)

把式(16)代入式(15)可得:

(17)

将效率对互感求导可得:

(18)

由式(16)—式(18)可知,当M取值满足式(16)时,系统功率达到最大值,此时效率小于50%,效率随着互感的增大而增大,根据实验中设定的参数其系统的功率和效率随互感变化的曲线如图5所示,当互感约为4 μH时,拾取功率最大。对于这种极松耦合的小体积多自由度拾取机构,效率不高,更注重于功率的拾取能力以及多自由转动过程中能量拾取的平稳性。

图5 系统的功率和效率随互感变化曲线Fig.5 Power and efficiency curves of system varying with mutual inductance

3.2 耦合机构参数优化

由式(8)可知,拾取机构的绕线匝数越多,互感越大,但拾取机构多自由度转动时,互感的波动也越大,说明能量拾取的平稳性越差。

通过COMSOL仿真,得到不同旋转角度下等效互感随着匝数N2的变化关系如附录A图A3所示,互感和旋转角度及匝数三者之间的关系符合前面理论分析,当N2=20匝时,互感波动较小,维持在4 μH左右。综上,当N2=20匝时,拾取功率最大且能量拾取较为稳定。

4 三维正交环形线圈与偶极线圈比较

传统的三维两两正交环形线圈也可以实现多自由度拾取,为了比较三维环形线圈和偶极线圈的多自由度拾取性能,利用COMSOL建立两者的仿真模型如附录A图A4所示,两种线圈所占用的空间体积、三维十字架磁芯结构、线径以及线的用线长度均一样。

在同等的发射条件下,两种线圈的等效互感如图6所示,偶极线圈的等效互感比环形线圈大得多,而互感又是影响功率和效率的重要因素,这就说明同等条件下,对于磁能拾取来说,偶极线圈的功率密度比环形线圈大。从磁场分析来说,由于偶极线圈在这种磁芯结构的引导下,能引导更多的磁力线穿过线圈平面,对磁场的空间捕获能力更强。

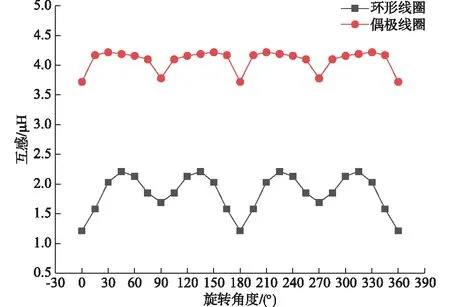
图6 两种线圈结构的等效互感随旋转角度变化的曲线Fig.6 Curves of equivalent mutual inductance of two coil structures varying with rotation angle

5 实验分析

耦合机构的实物如附录A图A5(a)所示,实验中的参数如附录A表A1所示,三维十字架骨架中嵌入了6个直径为8 mm、高度为25 mm的圆柱形磁芯。

系统的直流输入电压为10 V,全桥逆变产生高频交流电,谐振补偿后为副边提供交变磁场,3个拾取线圈感应电动势分别经过谐振补偿后,采用整流后串联模式输出电路见附录A图A5(b),其负载电阻为10 Ω。实际测得发射线圈的内阻为0.1 Ω,每个拾取线圈的内阻为0.08 Ω。当三维偶极拾取线圈自由摆放在发射线圈上方2 cm处,在不加控制的情况下得到3个偶极线圈的直流输出电压和负载电压如附录A图A6所示,示波器的第一、二、三、四通道分别对应3个拾取线圈整流后的电压V1,V2,V3和负载电压Uo。3个拾取电压之和为负载电压,根据负载电压Uo可计算出此时功率为16 W。

为验证三维偶极拾取机构多自由度拾取性能,测得负载电压随着旋转角度的关系如附录A图A7所示,负载电压在10～14 V之间波动,其输出电压较为稳定,可计算出在不加控制的情况下系统至少能拾取到10 W以上的功率。

6 结语

本文提出了一种采用三维偶极线圈的无线电能传输系统多自由度拾取机构,对无线电能多自由度拾取机构的设计提供了一个参考,对于提升拾取机构的灵活性具有重要意义,通过对系统参数的优化,在不需要复杂控制的基础上,可以实现较为稳定的输出。这种三维十字架形状的拾取机构适用于在空间内以各种姿态旋转的用电设备的无线充供电,特别适用于工业环境特定空间自由运动设备的供电(如工业机器人等),生物体内置电池装置的无线充供电(如智能药丸、胃肠道机器人等)。本文只是对该应用的可行性进行初步探索,接下来还需将拾取机构做小,提高功率传输效率。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。