以光伏为主的配电网储能容量需求的网格化场景评估方法
梁浚杰, 兰 飞, 黎静华
(广西电力系统最优化与节能技术重点实验室(广西大学), 广西壮族自治区南宁市 530004)
0 引言
在以光伏发电为主的配电网中使用储能设备,一方面能够减少光伏出力波动对电网造成的影响,提高系统运行的安全可靠性[1-2];另一方面可以对配电网中电能进行有效管理,达到更好的经济性效果[3-5]。但是,依据当前的技术条件,储能的容量受限且价格昂贵,因此如何合理确定储能容量是一个重要的研究课题。
目前对含光伏发电设备的配电网储能容量优化配置的研究,主要通过建立优化模型进行确定,其中多以电压波动最小[6]、系统经济性最好[7]、系统功率波动最小[8]等作为优化目标。例如:文献[9]以各节点电压越限量之和最小作为目标函数建立优化模型获得最优充电功率值,进而获取储能的最优容量配置;文献[10]以抑制光伏并网后系统节点电压波动为目标,在考虑需求侧响应的情况下对系统的储能容量进行优化配置;文献[11]以系统成本最小为目标建立优化模型,模拟不同容量规划下的分布式光伏并网运行情况,从而得到对应情景下最优的储能系统配置容量;文献[12]考虑储能充放电效率、荷电状态和全寿命周期成本等因素,建立了以经济性最优为目标的优化模型获取系统的最优储能配置容量;文献[13]提出两个衡量储能平抑风光储联合发电系统有功功率波动的指标,以功率波动指标最小为目标进行储能容量优化。
上述文献对储能容量的优化配置研究都是基于单一的衡量指标进行,为此,不少研究对此进行改进,在对储能容量进行优化配置时,考虑了对多个指标进行协调优化[14]。例如:文献[15]针对储能的选址定容问题构建了双层优化模型,分别以电压波动改善效果最佳与投资成本最小作为双层优化模型的两个目标进行优化;文献[16]以系统经济性最好和可靠性最高作为优化模型的两个优化目标建立优化模型,并使用双目标遗传算法求解得到储能容量的配置方案;文献[17]基于年调峰不足概率的技术性指标和基于年调峰费用的经济性指标,对可再生能源并网后系统对储能的需求进行评估;文献[18]在以系统总成本为目标构建储能优化模型时,不但对储能容量的优化配置进行了考虑,也对储能配置位置的优化进行了考虑。此类方法对系统的各项指标考虑得更为全面,然而较为复杂,不易实现。
以上研究为电力系统中储能容量的确定提供了良好的技术支持。然而上述文献所研究的配电模型中往往未考虑储能与常规机组、联络线、弃光等手段的协调配合,不能实现各种调节资源的综合利用。而且,当前的储能优化配置模型中决策变量较多,使得模型解算复杂,实用性受限。
基于上述问题,本文提出了一种实用的网格化场景分析方法。所提方法与工程上的短路电流运算曲线法理念相似。根据网格化的运行条件,计算不同运行条件下的技术性指标,生成给定场景下的技术性指标与储能容量的关系曲线图,然后根据给定的运行条件与运行要求获得系统对储能容量的需求。该方法可以在满足运行条件要求下,获得较好的储能配置方案,且计算简单、易于实用。
1 基于网格化场景的储能容量需求分析方法思路
基于网格化场景的储能容量分析方法的过程主要分为生成网格化场景、不同运行条件下技术性指标的计算、生成储能容量与技术性指标的关系图集合、储能容量需求的确定4个步骤。网格化分析的总思路见图1,下面分别对各个步骤进行介绍。

图1 网格化分析方法总体思路Fig.1 General idea of gridding analysis method
1)生成网格化场景
在以光伏为主的配电网运行中,运行条件包括与外网相连的联络线容量、储能容量和光伏渗透率等。其中本文对于光伏渗透率的定义为:全年光伏总发电量除以全年系统总用电量。将以上运行条件的取值进行组合可形成一个计算场景,而对这些条件选取不同的取值再相互组合,则可生成多个计算场景,形成计算场景的集合。其中网格化场景中每个运行条件的取值范围都在0与系统允许的最大值之间,通过在取值范围内进行等格划分,即可以得到各个场景中运行条件的取值。
在场景形成的过程中,涉及场景的精度和数量的权衡问题。如果各种运行条件的取值划分得太细,则计算场景数量太多甚至无法计算;如果运行条件的取值划分得太粗糙,则场景的精度难以保证。为此,本文采用网格化方法生成场景集合,网格化生成场景的方法在文中第2节进行详细介绍。
2)不同运行条件下技术性指标的计算
得到网格化场景后,建立技术性指标计算模型,计算不同运行条件下所有场景的技术性指标。本文采用的技术性指标为弃光率,对弃光率的定义为:全年弃光电量除以全年光伏总发电量。不同运行条件下技术性指标的计算模型与计算方法在第3节进行了详细介绍。
3)生成储能容量与技术性指标的关系图集合
计算得到技术性指标之后,即可得到一个包含四维向量(联络线功率容量、储能容量、光伏渗透率、弃光率)的数据集合。这个数据集合可以用M张弃光率与储能容量的关系图来表示,其中M的数值等于联络线功率容量和光伏渗透率的组合场景数目。如图1中的第3步内图形所示的关系图,其为光伏渗透率为a、联络线容量为b的运行条件下储能容量和弃光率的关系曲线。
4)储能容量需求的确定
获得给定联络线功率容量和光伏渗透率的场景下,储能容量和弃光率的关系曲线之后,即可以根据系统给定的光伏渗透率、联络线功率容量、弃光率要求来确定系统储能容量的需求。例如从图1中第3步内图形中的A点可知,在系统给定运行场景为:光伏渗透率为a、联络线功率容量为b,当要求弃光率小于Ln时,系统所需的储能容量至少为En。
2 网格化场景生成方法
2.1 生成方法的步骤
从第1节可知,本文方法对储能容量进行确定时,需要先生成网格化场景。本文生成网格化场景如图1中第1步内图形所示,具体过程如下。
1)分别将光伏渗透率、联络线容量、储能容量在其取值范围内进行等格划分。例如:图1中第1步内图形中,光伏渗透率的取值范围为0~Kmax,联络线功率容量的取值范围为0~Smax,储能容量的取值范围为0~Emax;将光伏渗透率分为3格4个取值,联络线容量的取值范围划分为3格4个取值,储能容量的取值范围分为3格4个取值。
2)组合光伏渗透率、联络线容量、储能容量的取值,即可得到一个场景。例如:图1中第1步内图形中标号为X的交点代表一个场景,该场景的光伏渗透率为Kmax,联络线容量为Emax,储能容量为Smax。
3)将所有的光伏渗透率、联络线容量、储能容量的取值进行组合,即可得到一个场景的集合。例如:图1中第1步内图形中,所有的立方格子的交点即代表了场景的集合,其中共有64个场景。
2.2 场景精度与场景数量之间协调的说明
在网格化场景形成的过程中,必须对场景的精度和数量进行权衡。如果选取的运行条件太多,或是运行条件的取值划分得太细,则会导致计算场景数量太多甚至无法计算;如果运行条件的取值划分得太粗糙,则场景的精度很难保证。因此,对于网格化场景中运行条件选取和取值划分问题,应尽可能地遵循如下原则。
1)选取网格化场景中所包含的运行条件时,若选取的运行条件过多,会导致网格化场景维度过高,其中包含场景过多。因此,除了必须选择的储能容量以外,另外选取的运行条件应以2~3个为宜。
2)为能较好地评估系统在不同运行条件下的储能容量需求,对储能容量在其取值范围内进行取值划分时,应选择进行较为细致的划分,一般需设置至少10个取值,以对储能容量进行较为精确的评估。
3)对其他运行条件进行取值时,对实际运行中需要考虑较多情况的运行条件,应进行较为细致的取值划分,以充分考虑实际运行中可能出现的各种情况;而对于相对固定或是所需考虑精度不是很高的运行条件,可进行较为粗略的划分,以减少网格化场景的数目,降低运算需求。
对于网格化场景数量随考虑的影响因素数量变化的情况,进行如下分析:假设只考虑储能容量有10个取值,其他的影响因素只考虑有3个取值时,此时当除储能容量分别考虑1,2,3,4个影响因素时,网格化场景中的场景数分别为30,90,270,810个;而当其他影响因素考虑有5个取值时,对应的总场景数为50,250,1 250,6 250个。可见,当考虑的影响因素增多时,场景数会呈指数性增长,特别是每个影响因素取值较多时,会大幅提高计算需求。因此在网格化场景生成的过程中,建议选择储能容量与其他2~3个影响因素,每个影响因素根据实际评估需要选取5~10个取值,在保证一定精度的情况下控制场景数量。关于网格化场景数量随考虑的影响因素数量变化的情况也可见附录A图A1。
3 基于网格化场景的技术性指标计算模型与方法
获得网格化场景集合之后,需要建立技术性指标的计算模型,将网格化的每个场景给定运行条件代入模型中,计算出技术性指标。弃光作为光伏发电并网后存在的主要问题之一,降低弃光率、提高资源利用率是配置储能的主要目的[19],因此本文中的技术性指标选择的是弃光率。技术性指标的计算模型如下。
3.1 目标函数
以系统弃光率最小为目标建立优化模型,模型的优化函数如式(1)所示,其中弃光率的计算公式如式(2)所示[20]。
F=minR
(1)
(2)
式中:R为弃光率;i为节点编号;N为系统节点总数;t为时刻编号;T为系统仿真的时间尺度;PDG,i(t)为第i节点第t时刻光伏发电的有功出力;Ploss,i(t)为第i节点第t时刻的弃光功率。
3.2 约束条件
1)各时段各节点的功率平衡约束
(3)
式中:PG,i(t)和QG,i(t)分别为第i节点第t时刻常规机组发电的有功和无功出力;PL,i(t)和QL,i(t)分别为第i节点第t时刻的有功和无功负荷功率;PE,i(t)为储能设备对第i节点在第t时刻的充放电有功功率;PT,i(t)和QT,i(t)分别为联络线对第i节点在第t时刻提供的有功和无功功率;ΔPi(t)和ΔQi(t)分别为第i节点第t时刻从线路获得的有功和无功功率,有
(4)
Vi(t)为第i节点第t时刻的节点电压;θij为节点i与节点j间电压的相角差;Gij和Bij分别为支路ij的电导与电纳。
2)配电网运行的节点电压与支路功率约束
(5)
(6)

3)联络线容量约束与常规机组出力约束
(7)
(8)
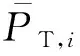
4)储能容量与储能充放电功率约束
(9)
(10)

5)系统弃光功率约束
0≤Ploss,i(t)≤PDG,i(t)
(11)
式(11)表示任一节点在任一时刻上弃光功率介于0与该时刻光伏发电功率之间。
3.3 基于给定场景的计算方法
根据3.1节介绍的模型目标函数以及3.2节介绍的模型约束条件,即可构建以弃光率最小为目标的配电系统优化运行模型。模型中的各时刻负荷功率、光伏发电出力使用历史数据或预测值,取时间间隔为1 h,1年共8 760个点的数据;线路阻抗参数、常规机组出力上限、支路功率上限、储能充放电功率上限根据实际系统获得;模型中的光伏发电出力、联络线容量上限、储能容量上限的数值,从网格化场景中的单个场景里设定的运行条件获得;而各时段弃光功率、各时段联络线功率、各时段常规机组出力、各时段储能功率出力作为决策变量。
在计算网格化场景中不同场景的技术性指标时,只需要根据不同场景中的运行条件替换模型中的光伏发电出力、联络线容量上限、储能容量上限的数值即可。这样就避免了在优化模型中将此类参数也作为决策变量进行优化,减少了优化模型中的决策变量数目,使得该优化模型的计算量较少。而模型的解算可调用CPLEX求解器求解。
通过上述方法计算网格化场景中的每一个场景的弃光率,即可得到在不同运行条件下配置不同储能容量时系统的弃光率,进而可根据弃光率的计算结果评估系统对储能容量的需求。
3.4 关于配置储能后经济性的讨论
在储能容量配置的过程中,系统的经济性也是一个十分重要的指标。而在建立储能容量的优化模型过程中,若同时考虑系统的经济性进行优化会涉及较多因素,使得模型过于复杂,不利于应用[12]。因此本文在对储能容量进行确定时,为了不使得优化模型过于复杂,优化模型中仅考虑了系统运行的约束与技术性指标要求,在规划过程中没有考虑系统的经济性。而对于配电系统的经济性评估,可以在通过优化模型确定储能容量之后,再根据规划好的储能容量进行计算以评估系统的经济性。
4 储能容量与技术性指标关系曲线图集合的生成
根据第3节介绍的模型计算得到每个场景的弃光率之后,可以生成不同运行条件下系统弃光率的计算结果统计,如表1所示。表中统计了光伏渗透率为K的情况下,系统中给定联络线容量和储能容量不同时弃光率的计算结果;E1,E2,…,En为储能容量的各个取值;S1,S2,…,Sn为联络线容量的取值;R11,R21,…,Rnn为对应运行条件组合而成的场景下计算得到的弃光率。

表1 数据关系示例(光伏渗透率为K)Table 1 Examples of data relationship (photovoltaic permeability is K)
得到弃光率的计算结果统计表后,即可根据表中数据绘制类似图1中第3步内图形所示的储能容量需求与弃光率的关系曲线图,将不同运行条件下的关系曲线图进行组合即可得到曲线图集合。曲线图集合中展示的是在不同运行条件下系统弃光率与储能容量的关系曲线集合,其中每幅图表示一个场景下弃光率与储能容量的关系曲线,每个场景的运行条件分别为:光伏渗透率K与表1中不同联络线容量的组合。表1中给定了n个联络线容量的取值,因此该集合中包含了n张关系曲线图。同样可由网格化场景中其他光伏渗透率下技术性指标的计算结果,通过上述方法获得不同渗透率下的曲线图集合。关系曲线图集合的形式可见附录A图A2。
5 给定场景下的储能容量需求确定
在获得每种运行条件下储能容量与弃光率的关系曲线图之后,即可根据给定的运行条件与运行要求,确定系统所需要的储能容量,具体步骤如下。
1)确定系统给定的运行条件,从关系曲线图中选取出对应运行条件下的储能容量与弃光率的关系曲线图。
2)在选取出的关系曲线图中,根据弃光率的运行要求,根据第1节中介绍的方法确定在此弃光率要求情况下系统所需的储能容量。
例如,当需要确定运行条件为光伏渗透率K,联络线容量Sn,系统运行要求为弃光率0%时的储能容量需求时,需要先根据给定的运行条件选取出对应的储能容量与弃光率关系曲线图;再根据给定的弃光率要求,从选取出的曲线图获得光伏渗透率为0%情况下对应的储能容量作为储能容量需求的确定结果。
6 算例分析
本文以改造之后的IEEE 33节点配电网为例,应用所提出的网格化场景分析方法,对系统接入光伏发电后对储能容量的需求进行分析评估。同时,对评估得到的储能容量代回配电网中进行运行模拟,验证评估得到的储能容量是否能满足运行要求。
6.1 算例说明
IEEE 33节点配电网数据与拓扑图详见文献[21],本文改造如下:在节点9~33接入光伏电源;系统中包含了6个储能装置,储能装置1与节点9~13相连、储能装置2与节点14~18相连、储能装置3与节点19~22相连、储能装置4与节点23~25相连、储能装置5与节点26~29相连、储能装置6与节点30~33相连,储能设备可与和其相连的节点进行功率交互;节点1通过联络线与外网进行功率交互。仿真采用的负荷序列数据为中国某地实际负荷序列,光伏出力序列则是使用HOMER软件生成,序列数据采样间隔为1 h,即一天24点、全年8 760点的数据。
针对所采用的仿真算例,生成如下的网格化场景:选取光伏渗透率、储能容量、联络线容量作为网格化场景的3个维度,其中光伏渗透率的取值为30%,50%,70%,100%;储能容量取值范围为0~18 000 MW·h并分为13个取值;联络线容量的取值范围为0~120 MW并分为10个取值;储能功率、常规机组功率上限、系统仿真的时间尺度作为常量处理,储能总功率上限设置为40 MW、常规机组功率上限设置为50 MW、仿真时间尺度设置为1年8 760 h。由如上设定可生成共有520个场景的网格化场景集合,根据生成的网格化场景,即可选取网格化场景集合中各场景的运行条件代入第3节的模型进行计算,获得不同运行条件下储能容量与弃光率的关系曲线集合。改造后的IEEE 33节点配电网拓扑见附录A图A3。
6.2 系统在不同运行条件下的储能容量需求分析
针对算例给定的配电网,以表2给出的不同运行条件与运行要求组合而成的场景为例,对不同场景下配电网对储能容量的需求进行分析计算。

表2 用于储能需求分析的仿真场景Table 2 Simulation scenarios for energy storage requirements analysis
对应表2中5个场景中给定的运行条件,从网格化场景的弃光率计算结果中,选出对应场景下的储能容量与弃光率的关系曲线如图2所示。图2中各个子图与表2中场景的对应关系为:图2(a)对应场景1,图2(b)对应场景2与场景3,图2(c)对应场景4,图2(d)对应场景5。根据每个场景的储能容量关系曲线图结合各个场景的弃光要求,即可得到对应各个场景需求的储能容量。
从图2中弃光率随储能容量变化的曲线可见,当系统的光伏渗透率越高、联络线容量越小、要求弃光率越小时,系统对储能容量的需求越大;同时可见弃光率随储能容量增加而变化的曲线成“L”形,即当弃光率较高时,提高储能容量可以有效地减少系统的弃光率,而当弃光率较低时,提高储能容量对减少弃光率的效果较差。
根据图2和表2中的运行要求,可以得到各个场景的储能容量需求。根据图2(b)中的曲线可见,在系统光伏渗透率与联络线容量相同的情况下,适当放宽弃光率要求可以有效减少系统对储能容量的需求。例如:对于场景2与场景3,在同样的运行条件下,要求的弃光率从10%减少到5%时,系统对储能容量的需求从347 MW·h上升到了6 940 MW·h,储能容量需求上升了20倍而弃光率只减少了5%,这显然是不经济的。

图2 不同场景的关系曲线Fig.2 Relationship curves in different scenarios
6.3 储能配置方案的评估
为说明本文所提方法的有效性,以表2中的场景1为例,根据图2的储能容量需求分析结果配置对应容量的储能设备,对配置储能后的系统在给定场景下进行运行模拟来评估储能配置后的效果。其中运行模拟使用的数据采用对6.1节中仿真采用的负荷与光伏出力数据改造后得到,改造方法为将每个时段原始的负荷与光伏出力数据乘上一个0.9~1.1之间的随机数,模拟负荷与光伏发电出力的随机性。根据改造数据进行时间尺度为1年8 760 h的模拟运行,根据模拟运行得到的储能运行结果、弃光率计算结果与节点电压运行结果对储能的配置方案进行评估。
1)储能运行结果的说明
为了验证储能设备能够按所给定的约束正常运行,首先给出模拟运行时系统中储能设备在全年储存电量的变化曲线与1月储能的充放电曲线。其中全年储存电量的变化曲线如图3(a)所示,1月储能的充放电曲线如图3(b)中所示。

图3 储能仿真结果Fig.3 Simulation results of energy storage
由图3(a)所示的储能全年电量变化曲线可见,储能中存储的电量在全年都保持在储能容量上限的0.25~0.95之间,在0~1 000 h与7 500~8 760 h时段内,储能电量接近储能允许存储电量的下限,在4 500~6 500 h时段内,储能电量接近储能允许存储电量的上限,满足储能的运行约束。图中还可见,储能中电量发生变化的主要时段是在3 000~4 500 h与6 500~7 500 h这两个时段,其他时段中储能电量均变化不大。
由图3(b)给出的储能充放电功率曲线可见,储能的充放电功率均在给定的储能功率(40 MW)范围内。结合储能设备在全年存储电量的变化曲线进行分析,1月储能的电量多接近储能电量允许值的下限,因而图3(b)中储能设备在一日内的动作均为先在光伏出力较大的时段进行充电,再在光伏出力较小的时段将电能放出。
通过以上分析可知,储能设备均按照给定约束运行,在模拟运行中储能设备可以正常动作。而增设储能设备的目的是帮助系统消纳光伏发电出力,降低系统的弃光,接下来进一步分析配置储能设备后系统的弃光情况。
2)弃光率结果说明
根据对系统全年的运行仿真,可以得到系统全年的弃光电量与全年的光伏发电量,用以判断是否符合系统的弃光要求。根据运行仿真可得到系统全年的光伏发电量为212 GW·h,而弃光电量为10 GW·h。计算可得,系统进行全年的运行仿真后得到的弃光率为4.52%,符合表2中场景1给出的运行条件:弃光率小于5%的要求,证明了所提出的储能配置方法的有效性。
同时根据获得的弃光计算结果,发现系统中有弃光功率的时段主要集中在4 000~6 000 h之间,而观察图3(a)中储能电量的变化曲线,可见此时段内储能电量已经接近其上限,这说明当储能中没有足够容量存储多余光伏发电的电能时,系统会发生大量的弃光现象。模拟运行时全年的弃光功率曲线见附录A图A3。
3)节点电压运行情况说明
6.1节的仿真分析中,配电网在运行时要求系统中各个节点的电压标幺值在0.95~1.05之间。为了验证在系统配置储能设备后,在运行时是否能够满足系统的节点电压约束,对系统中全年各个节点上出现的电压标幺值的最大与最小值进行校验。在全年的运行模拟中,节点18上出现过的最大电压标幺值在所有节点中最大(1.05),节点33上出现过的最小节点电压标幺值在所有节点中最小(0.98)。因此,系统中各个节点在模拟运行时的变化范围均在0.95~1.05之间,满足系统的节点电压约束,证明在模拟运行时系统正常运行,也说明了按本文所提方法确定并配置系统储能容量,系统可以在满足弃光率要求的同时满足节点电压约束。系统中各节点在运行仿真中出现的最大最小电压分布曲线见附录A图A5。
7 结语
本文提出了一种实用的网格化场景分析方法,用以解决以光伏为主的配电网对储能容量需求的评估问题。所提方法减少了储能评估模型中的决策变量,使得模型易于解算,通过多场景仿真的方法评估系统对储能的需求。以改造的IEEE 33节点配电网作为示例,并采用所提方法确定了系统的储能需求,将评估得到的储能容量代回系统中进行了运行模拟证明方法的有效性,得到以下结论供参考。
1)所提方法能够获得满足给定运行条件与运行要求下的储能容量需求,减少了储能规划模型中的变量数,使得模型易于解算。
2)增设储能设备来减少系统的弃光率有效且可行,但是根据对储能容量与弃光率的关系曲线观察可见,当系统弃光率较高时,提高储能容量可以有效降低系统的弃光率,而当系统弃光率较小时,提高储能容量对减少弃光率的效果较差。
本文提出的方法可以获得在给定运行条件和运行要求下配电系统对储能容量的要求,帮助确定各种调节手段的优化组合方案,供规划和调度运行借鉴参考。但是本文所做的工作仍存在以下不足。
1)由于本文方法属于一个整体的切片方法,优势在于解算和分析,但是精度有一定误差,所得的储能配置方案不一定是最优解。
2)在设置网格化场景的过程中,如果设置的运行条件过多会导致网格化场景数量成几何倍数增长,极大地提高了计算量,因而不适合同时考虑过多的影响因素。
基于上述所分析的本文工作的贡献与不足,之后作者也将进一步研究该方法的改进方案,以提高该方法获得的储能需求容量精度并使其可有效考虑多个运行条件。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

