最小偏向角测定折射率实验改进
杨 慧,菅在和
(忻州师范学院 物理系,山西 忻州 034000)
0 引言
分光计是1814年夫琅和费为研究太阳暗线时在当时观察仪器上改进而来的,其设计思想和基本原理是现代光谱仪摄谱仪设计制造的基本依据.分光计可以用来测量反射角、折射角、最小偏向角等[1,2].折射率是光学材料的一个非常重要的参数,通过研究物质的折射率,可以更好地研究、应用该物质.所以很多学者对最小偏向角测量折射率的实验进行了改进[3-6],但测量最小偏向角时,往往找到的是一个微小范围内的值,不能精准确定最小偏向角.
本文将以实验法为基础方法,通过引入水准仪、平面镜、薄铁片、游标卡尺、用两块薄铁片确定入射光与反射光的平行程度来精准确定最小偏向角并数据处理时引入C++语言来替代人工处理来提高计算准确度.
1 最小偏向角测量三棱镜折射率的理论推导

图1 最小偏向角原理图
因最小偏向角测量晶体、溶液和三棱镜折射率的过程相似,原理一致,下面将以测量三棱镜折射率为例进行分析改进
图1所示为一块三棱镜,角A为折射棱角,当单色光束射向棱镜,会发生两次折射,将出射线和入射线之间的夹角δ称为偏向角.
δ0=2i-A
(1)

i1=(δ0+A)/2
(2)
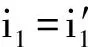
(3)
所以利用这俩个特殊的入射角和折射角,就可以计算棱镜材料的折射率:
(4)
根据上述只需测出最小偏向角和三棱镜的顶角,三棱镜的折射率便可确定[2].

表1 最小偏向角数值
2 最小偏向角测量折射率实验的误差分析及改进方法
2.1 最小偏向角测量折射率实验的误差分析
大学物理实验中最小偏向角是通过目测观察确定的.所测得的数据都是比最小偏向角的实际值要大的,如表1所示实验随机测了十组数据,通过这十组数据中的每组数据的最大值与最小值的差,可以看出目测度数误差还是很大的.
通过几何光学知识和图1我们可以得出偏向角δ与入射角i的关系式如下[7-9]:
上式中的n是三棱镜的折射率,A是三棱镜的顶角.将上式表示到坐标轴上.其中n为1.6,A为60°.就可以发现在曲线的最低点周围有一段斜率基本趋于0的曲线,它们的取值都近似于最小偏向角,但是实际值都大于最小偏向角.实验的时候,进行操作时大多情况下望远镜还没转到最小偏向角时就停下或已经转动望远镜超过它后才停下,这就导致,目测的数值不是精准的最小偏向角,从而导致求折射率时产生误差.
2.2 最小偏向角测定折射率实验改进
2.2.1 两块薄铁片确定入射光与反射光平行程度
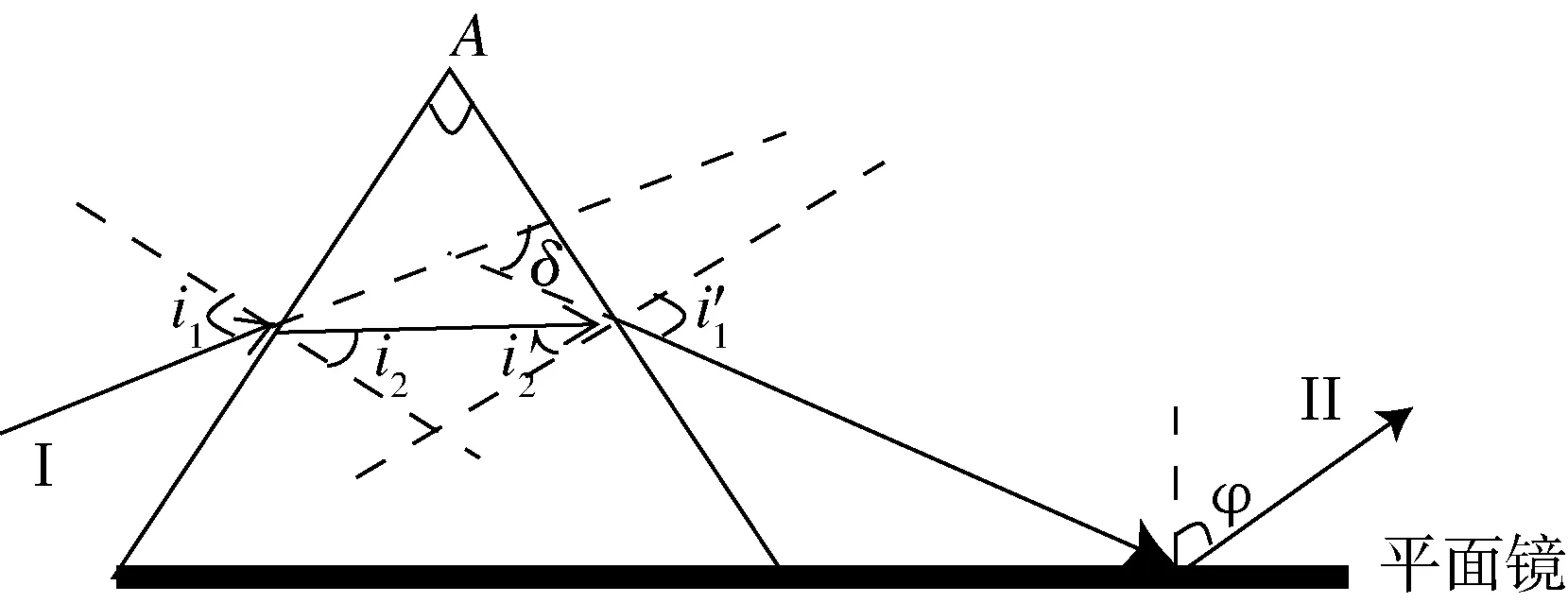
图2 新最小偏向角测量原理图
通过引入平面镜、薄铁片、游标卡尺等工具,将图2中的入射光Ι与反射光ΙΙ调节平行从而精准确定确定最小偏向角.
2.2.2 两块薄铁片确定入射光与反射光平行程度测量最小偏向角的原理
如图1所示,当入射光束Ι与反射光线ΙΙ平行时,此时的偏向角达到极小值,即最小偏向角.以下是证明过程:根据(1),(2),(3)的推导可知,我们可以得出:
(5)
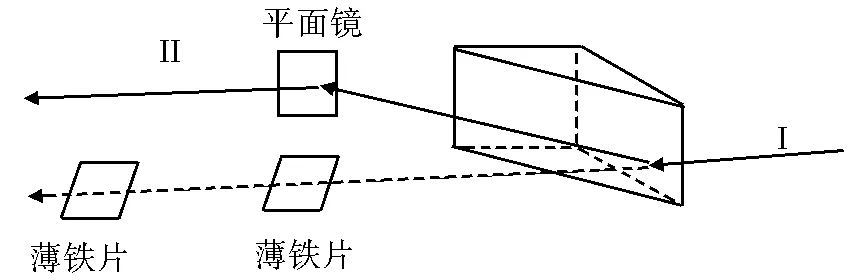
图3 测量最小偏向角新方法示意图
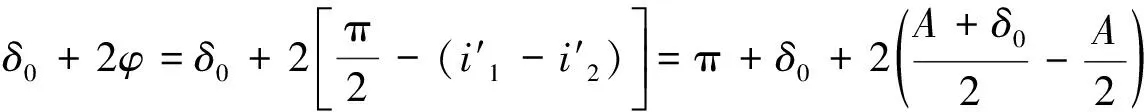
(6)
改进后的实验精准的判断出最小偏向角的位置了,以下是折射光线与入射光线平行的具体实验操作.
2.2.3 薄铁片确定入射光与反射光平行程度具体方案
该方案一是在三棱镜顶角A正对的棱镜面上增加一块长度大于棱镜底边长度的平面镜,作用:对光线ΙΙ进行反射;二是入射光Ι的延长线上增加两个光具座和两块薄铁片,光具座的作用:固定薄铁片,两块薄铁片的作用:记录入射光线Ι的路径;三是游标卡尺,作用:测量薄铁片到反射光的距离.
实验步骤:首先打开氦氖激光器,调节激光光束,使光束路径穿过载物台的中央,望远镜前镜将激光反射,使激光器的出射口附近可以看到光点,若光点不能恰好落在激光器的出射口,就调节激光器的高低俯仰,直至光点恰好落入激光出射口[10].此过程不要用眼睛直视激光,否则会对眼睛造成伤害.调节完成后,激光光束与目镜是在一条直线上的.此时,就需要把激光光束的路径记录下来并记下角度值.记录光束路径比较困难,因为光束可见不可触,所以要用替代法将光束路径记录下来.可以用两个光具座分别固定一个薄铁片,缓慢的调节薄铁片的位置使两块薄铁片都在激光光束的路径上,再分别慢慢移动薄铁片,使薄铁片的俩侧都可以看到宽度都一样稀疏的红光.最终使两块薄铁片都要在光束路径上,并且两快薄铁片两侧的红光都要基本一样.完成这些后将光具座上的螺丝固定.这样激光光束的路径就被记录了下来.
然后将三棱镜放置到载物台的中央,再将准备好的平面反射镜紧贴顶角A所对的底边,使折射过来的激光光束可以发生反射,此刻光束可以打到不远处的墙上.转动紧贴平面镜的三棱镜,可以清楚地看到墙上的光点随着三棱镜的转动而移动着,转到经折射和反射的光束路径离调节好的薄铁片比较近的时候停止转动,再对入射角进行细微的改变,用游标卡尺测量薄铁片到激光光束的距离,两块薄铁片到激光光束的距离都一样即可.如图2.2所示.此时的偏向角即为最小偏向角.在记录数据时将三棱镜固定,然后撤去平面反射镜,记录此时的入射角和出射角即可
3 改进前后的实验数据处理与分析
3.1 改进前的实验数据处理与分析
见表2、表3.
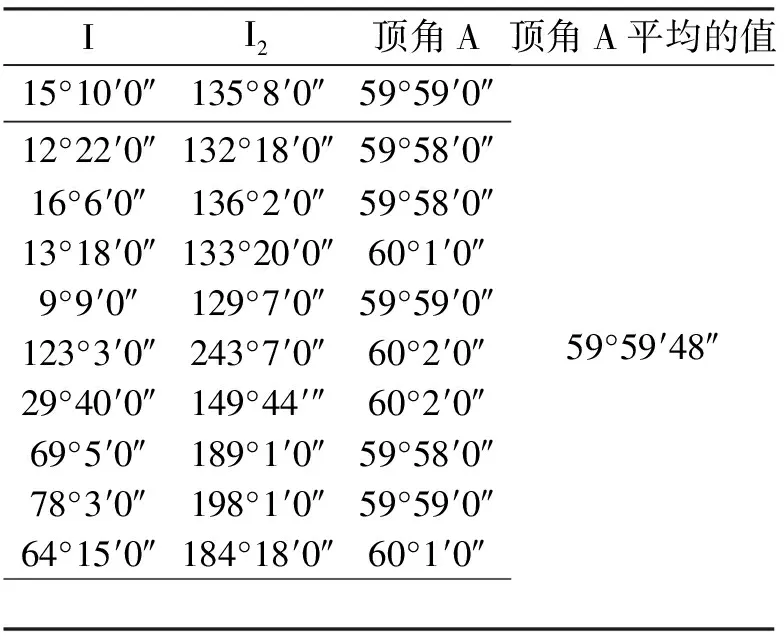
表2 实验测量的顶角数据

表3 改进前实验测得的最小偏向角数据
实验用时较长.测得的折射率为比真实的大0.098,百分误差为6.13%.可以得出误差较大.
3.2 改进测量方法后的实验数据处理与分析

表4 改进后实验测量的顶角数据
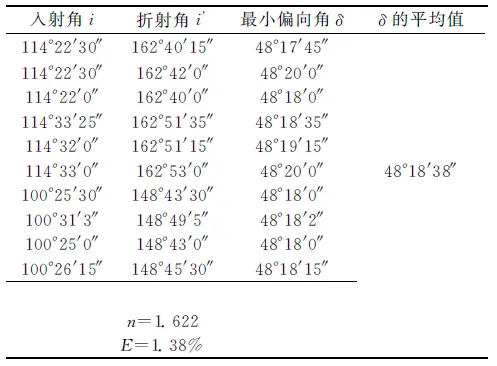
表5 改进后的实验测得的最小偏向角数据
改进后的实验用时明显减少.测得的折射率比真实值大0.022,百分误差为1.38%.改进后的实验误差明显降低,见表4,表5.
4 结束语

表6 原实验与改进后的新实验数据比较
本文主要通过对最小偏向角测量折射率实验进行分析研究,找出一大缺陷:测量最小偏向角时,往往找到的是一个微小范围内的值,不能精准确定最小偏向角,通过引入两块薄铁片确定入射角与反射角的水平程度来精准确定最小偏向角(应用等效替代法引入两块薄铁片代替激光路径);
改进组成一种全新的测量折射率的方法.
从表6可看出,改进后的新实验在用时上明显缩短,测量的折射率准确度明显提高很多,百分误差也明显减少很多.所以分光计实验中最小偏向角测量折射率实验这样改进是有效的.

