基于蛙跳算法的Mesh网络最优路径
邵伯乐
(亳州职业技术学院,安徽 亳州 236800)
0 引言
Mesh网络是一种高速率和低成本的无线网网络,并随着IEEE802.11和无线网络快速发展获得广泛应用[1-2].Mesh网络能根据具体的业务需求而进行定制,能充分利用无线局域网和无线自组织网络的优点,其应用范围也多种多样,如可以用于组建家庭宽带网、用于构造区域网、用来建立公共紧急通信和战场通信等[3].在传统的无线网络中,网络质量和负载影响了网络的吞吐量,而Mesh网路由于具备较高的传输速率、较大的覆盖范围、方便的架设方法以及完美的容错能力,已被认为是无线组网技术中的最优前途的技术之一[4].
Mesh网络作为一种无线网络,当数据传输的路径发生阻塞或中断时,Mesh网络仍然会面临着数据包丢失的问题.为了获得更优的路径,一些文献提出一些方法来改进Mesh网络的最优路径.如乔宏等[5]提出了一种实现网络公平协作的路由算法,将该问题转换为最大化网络整体效用的凸化问题,利用对偶分解和子梯度来实现mesh网络的公平路由.沈小建[6]等提出了一种基于编码感知和负载均衡的多播路由,基于负载均衡路由量来综合考虑节点通信密集度和网络拥塞程度,仿真实验该协议能在提高吞吐量的前提下进行网络编码,实现负载均衡.张维维等[7]提出了一种基于博弈论和无线Mesh网络路由与信道分配联合优化算法,通过建立极小极大合作纳什均衡信道分配方案,并对博弈算法和贪婪算法对网络吞吐量的影响进行比较.邓晓衡等[8]提出了一种基于链路质量与负载敏感的无线Mesh路由协议,在该协议中考虑链路多速率和负载动态性,以对链路的质量进行准确评估.符琪[9]提出了一种基于业务感知的多路径Qos路由策略,通过4个固定信道的竞争参数的AC队列来实现不同业务数据包的存储转发,通过改进信道竞争的分配参数来提出不同业务数据类型的路由判断,该策略能实现不同业务流的信道和链路的公平使用.
以上工作均着眼于建立Mesh网络的最优路径,并对其优化,然而这些工作均以优化整个路由为目标,未对其中的路径的最优化策略进行考虑[10],因此,提出了一种基于蛙跳算法和神经网络的Mesh网络最优路径,并通过实验证明了所提方法的正确性.
1 改进的蛙跳算法
1.1 蛙跳算法概述
蛙跳算法是由Eusuff和Lansey提出的混合蛙跳算法(Shuffled Frog Leaping Algorithm, SFLA),是在模因演化算法和粒子群算法的基础上发展而来,该算法结合了这两种方法的优点,能广泛地应用于非线性、不连续、多目标和不可导问题.
随机采取定义域内的N只青蛙作为初始种群,第i只青蛙的坐标为xi={xi1,xi2,xi3,…,xin},将整个青蛙种群随机划分为a个种群,每个种群包含的个体数为b,则青蛙的总数和各个种群之间的关系满足:
N=a*b
(1)
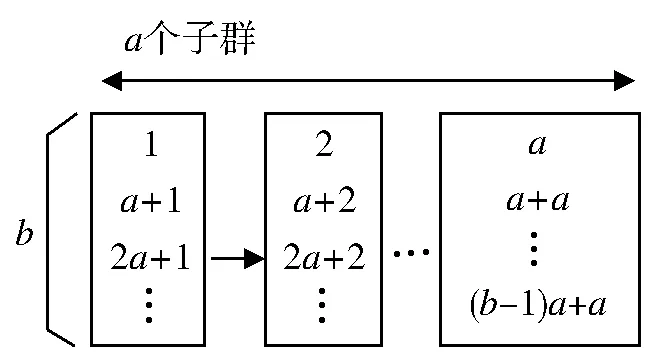
图1 种群总体与子种群的关系
种群总体与各子种群的关系如图1所示.
1.2 改进蛙跳算法
在每轮迭代中,适应度最优的个体和最差的个体分别记为po和pw,而整个种群中的最优个体为pg,则种群个体pw被更新为:
p=pw+α(po-pw)
(2)
其中,p表示新一代种群中的个体,而α为学习率,即新的个体在最差适应度个体的基础上,要进行的改进.此时,计算个体的适应度,如果p的适应度小于pw,则在新的种群中采用p来替代pw,重复以上过程,直到局部搜索次数达到最大值.
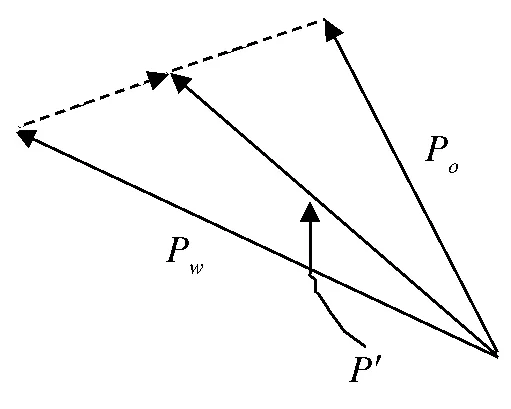
图2 青蛙个体更新方法
除最差个体外的其他个体的更新方法如下:
p=(1-C)po
(3)
其中,C的值域为大于0并小于1的可调参数.当其值随着算法进行不断变化时,会对算法产生影响.当该值设置合理时,设置为较小的值,以充分利用最优值的信息.随着迭代次数的不断增加,青蛙的个体差距进一步降低,此时如果将C设置为较小的值,算法容易陷入局部最优.C值的更新可以表示为:
C=1-e-20*(t/tmax)L
(4)
其中,参数t表示当前迭代次数,tmax表示最大的迭代次数,L为调整参数.
基于以上改进的青蛙个体更新方法,则改进的蛙跳算法如图3所示.
2 基于改进蛙跳算法的mesh网络路由获取
该算法将网络中的所有节点分为若干的簇,分簇协议采用Leach协议,然后再通过改进的蛙跳算法来建立多个簇头之间的多跳路由.

图3 改进的蛙跳算法
2.1 簇的个数
该算法根据Leach协议将网络分为若干个簇,簇头的数量根据下式来确定:
(5)
其中,参数εfs表示自由空间传播模型对应的功率放大所需的功耗系数,参数εmp表示多路衰减传播模型下功率放大所需要的功耗系数.
2.2 路由优化算法描述
为了采用蛙跳算法来获取最优路由,首先需要定义适应度函数,这里设计的适应度函数为:
(6)
其中,β和γ表示权重因子,β+γ=1,E为传感器节点的剩余能量,E0为传感器节点的初始能量,dmax为种群中所有个体距离基站的最大距离,dσ为该传感器到基站的距离.
采用改进的蛙跳算法来实现mesh网络的多簇路由的算法可以定义为:
算法1 基于改进蛙跳算法最优路由算法
初始化: 参数β和γ, 调整参数L,种群的个数a,每个种群包含的个体数b;
步骤1: 个体编码:根据簇的数量确定个体的位数,确定个体的编码的长度;
步骤2: 生成种群:根据种群的编码随机生成初始种群,并划分为多个子种群,子种群个数为a,每个子种群包含的个体数b;
步骤3: 根据公式(6)计算种群个体的适应度,根据适应度对种群中的所有个体进行排序,将适应度最优的个体和最差的个体标记为po和pw,整个种群中的最优个体为pg;
步骤4:对每个子种群中最差的个体采用公式(2)进行更新;
步骤5:对子种群中的其他个体按照公式(3)进行更新;
步骤6:判断算法是否已经达到最大的迭代次数:
如果已经达到,则算法结束;
否则返回步骤3继续进行迭代.
3 仿真实验
为了对本文提出的方法进行验证,采用NS2工具来产生实际mesh网络最近似的无线拓扑结构,然后对其扩展,使其能进行网络编码.Mesh网络的总节点数为100个,仿真的区域为1 000*1 000的区域,分别对不同负载对应的路由时延、吞吐量和带宽消耗总量.仿真参数为:苏剧分组大小为1 000字节,节点传输范围为200m,节点的干扰半径为100 m,节点的传输带宽为10 Mbit/s.将文中方法与文献[6],文献[7]和文献[8]进行比较,4种方法得到的网络吞吐量的比较如图4所示.
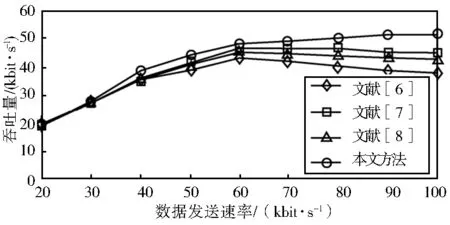
图4 网络吞吐量比较

图5 时延比较
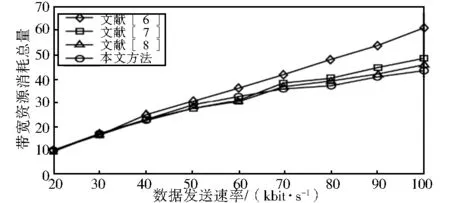
图6 带宽消耗总量比较
图4为4种方法的网络吞吐量与网络负载之间的关系,从中可以明确看出本文方法的网络吞吐量远远大于其他三种方法.其原因可能是本文方法通过优化了传输路由,缩短了传输路径,从而使得网络的总吞吐量更大.
网络吞吐量与时延的关系如图5所示,从图中可以看出,4种方法的路由时延随着网络传输数据量的增加而逐渐增加,但相对于其他3种方法,本文方法的路由时延较慢,这是因为优化的数据传输路径使得总的传输时间减少,因此,使得网络的总时延大大降低.
带宽总耗量与数据发送速率之间的关系如图6所示,与前面仿真的时延和网络吞吐量类似,带宽总耗量也随着数据发送速率的增加而逐渐增大,但本文方法增加的最少.

