基于一维超导体光子晶体的可调光波反射器的设计

黄 蓓,王晓华

(1.盐城师范学院 新能源与电子工程学院,江苏 盐城 224007;2.盐城盐兴机动车检测有限公司,江苏 盐城 224015)

0 前言

1987年,Yablonovitich和John分别从“抑制自发辐射”和产生光波的“局域化”的角度出发[1,2],几乎同时独立地提出了“光子晶体”．光子晶体就是不同折射率的材料呈周期性排列的人工微结构,根据其空间尺寸,可以分为一维、二维和三维等光子晶体．由于电磁波在其内会产生布拉格散射干涉,从而对入射的电磁波就会形成光子禁带的特性,利用这个特性,对光子晶体的研究日益增多[3-5]．不过,很多光子晶体一旦制成,其光子禁带就不可调．并且,从制备角度出发,一维光子晶体要比二维或三维的光子晶体要简单．因此,对一维可调控的光子禁带的研究变得十分有意义．

2004年,Hojo和Mase把等离子体和介质材料组成一维等离子体光子晶体,利用等离子体的折射率可以受其电子密度影响,通过对一维等离子体光子晶体的色散关系求解,从而得到其可调控的光子禁带[6]．2013年,章海锋把超导体引入不同结构的一维光子晶体中,形成一维超导体光子晶体,利用超导体的介电常数可以受温度调控,从而得到温度调控的光子禁带或高反射率[7,8]．利用超导体的低损耗和介电常数可调性,很多研究人员把超导体和不同折射率材料,如超材料[9]、半导体[10,11]或普通介质材料[12,13],组成各种一维超导体光子晶体,用传输矩阵法计算其反射率或透射率,实现了在不同频率范围内可调控的反射器或滤波器,为制备新型的光子晶体应用器件提供了理论研究基础．

图1 一维超导体光子晶体(AB)N反射器的结构示意图

我们课题组也先后把单负材料[14]、石墨烯[15]或半导体GaAs[16]分别组成不同的一维光子晶体,通过传输矩阵法计算其透射率,利用这些材料的介电常数或磁导率受外部参数的可调控性,从而得到可调控的多通道或单通道的滤波器．另外,我们用超导体YBa2Cu3O7(YBCO)和半导体Ge组成的隐身斗篷,利用超导体YBCO的介电常数受外部温度的调节,通过散射取消的隐身理论计算和电磁软件的数值仿真,实现了温度调节的宽频隐身[17]．本文,我们用超导体YBCO和半导体Si组成一维超导体光子晶体,通过调整超导体YBCO的厚度、电磁波的入射角和极化关系等外部参数,还利用超导体YBCO的介电常数受外部温度的调节,利用传输矩阵法计算其反射率,经过数值仿真从而实现可调控的光波反射器．

1 理论模型

图1是本文的一维超导体光子晶体(AB)N反射器的结构示意图,其中A是半导体Si,B是超导体YBCO,N是周期数．在可见光频率范围内,半导体Si的折射率是3.3．根据文献[17],基于双流体模型,超导体YBCO是高温超导体,并且其损耗可以忽略不计,则可以推导出超导体YBCO的相对介电常数εr随外部温度T和波长λ的变化关系公式如下:

(1)

根据文献[17]可知公式(1)的参数:居里温度Tc=93 K,伦敦穿透浓度在T=0 K时λL(0)=145 nm和高温超导体p=2．

当电磁波以θ角斜入射到一维超导体光子晶体中,其任意层l的传输矩阵的表达式如下[18]:

(2)

(3)

那么,对于多层材料的传输矩阵的表达式:

(4)

式中多层的特征矩阵M=M1M2…MN-1MN．可以得到该一维超导体光子晶体的反射系数r与反射率R:

(5)

2 结果与讨论

在可见光波长范围(350-800 nm)内,一维超导体光子晶体(AB)N反射器结构中,半导体Si的介电常数并不随外部温度变华而变化．根据公式(1),可以绘出图2是无损超导体YBCO的相对介电常数被外部温度进行调节的关系图．由图2可以发现,在超导体YBCO的居里温度下,其相对介电常数的在同一波长下,随着外部温度增加而略微增加;且其相对介电常数在外部温度不变的情况下,随着波长增加而略微减小．说明在超导体YBCO的居里温度下,其相对介电常数是可以受外部温度进行略微调节的．

图2 超导体YBCO的相对介电常数随外部温度与波长变化的关系图

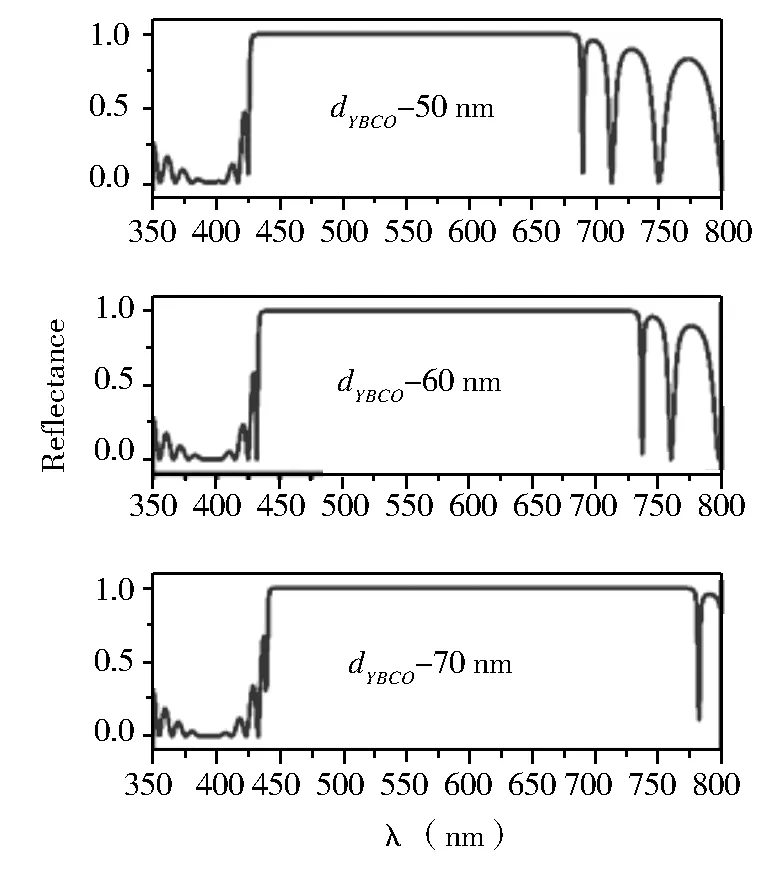
图3 在部温度T/Tc=0.5时,超导体YBCO厚度的变化对(AB)N结构的正入射电磁波反射率影响关系图

本文是用传输矩阵法研究一维超导体光子晶体air/(AB)N/air在可见光波长范围内的反射特性．因此,先设定在外部温度T/Tc=0.5与电磁波正入射时,半导体Si厚度为60 nm,周期数N=15,超导体YBCO厚度的变化对该结构反射率的影响,如图3所示．由图3可见,该结构对正入射的电磁波能产生较宽的光子禁带,也就是近于1的全反射波宽:在dYBCO=50 nm时,λ=260 nm;在dYBCO=60 nm时,λ=318 nm;在dYBCO=70 nm时,λ=338 nm．同样,可以发现随超导体YBCO厚度增大,光子禁带是向长波的方向偏移,也就是发生红移．因此,该一维超导体光子晶体air/(AB)N/air可以用来制成宽频的光波反射器．

根据图3,取超导体YBCO厚度为60 nm,其他条件与图3一样,下面讨论电磁波入射角的变化对一维超导体光子晶体air/(AB)N/air结构反射率的影响,计算结果见图4．由图4(a)可以发现,用该结构制成的反射器对TE模式的任何入射角电磁波能产生很好的较宽的光子禁带,也就是近于1的全反射波宽λ≥305 nm,并且随入射角增大,光子禁带是向低波的方向偏移,也就是发生蓝移;同时图4(b)可以发现,用该结构制成的反射器对TM模式电磁波能在低入射角时也能产生较宽的光子禁带,随入射角增大,与TE模式电磁波的变化趋势一样:光子禁带也是向低波的方向略微偏移,也就是发生略微蓝移．不过随入射角增大,光子禁带的波宽迅速减小．这就表明,用该结构制成的反射器对入射电磁波的极化较敏感．

图4 在部温度T/Tc=0.5时,电磁波入射角对(AB)N结构的反射率影响关系图:(a)TE 波;(b)TM波

根据上面的讨论,取电磁波入射角θ=45°,其它条件与图4一样,下面讨论外部温度的变化对一维超导体光子晶体air/(AB)N/air结构反射率的影响,计算结果见图5．在组成该结构的材料中,只有超导体YBCO的介电常数能被外部温度进行调节．由图5可以发现,该结构对45°入射角的两种模式电磁波都能产生较好的较宽的光子禁带,也就是近于1的全反射波宽:在TE波,λ=309 nm;在TM波,λ=157 nm．虽然,TE 波比TM波产生的光子禁带要宽,不过,两种模式产生的光子禁带对外部温度的变化很不明显．在图2中,分析认为超导体YBCO的相对介电常数虽能被外部温度调节,不过变化很小,也就是超导体YBCO的折射率随外部温度变化很小,因此造成该结构的反射率对外部温度的变化不明显,这个结论与文献[12]一致．

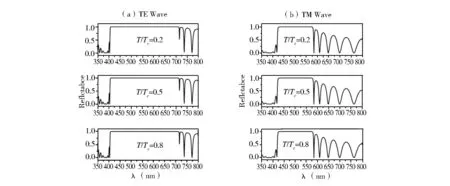
图5 在电磁波入射角θ=45°时,外部温度对(AB)N结构的反射率影响关系图:(a)TE 波;(b)TM波

3 结论

本文用半导体Si和超导体YBCO组成一维超导体光子晶体,利用传输矩阵法对air/(AB)N/air(其中A是Si和B是YBCO)的反射特性进行了理论推导与数值模拟仿真研究．通过数值模拟仿真,发现该结构对正入射的电磁波能产生较宽的光子禁带,即近于1的全反射波宽随着超导体YBCO的厚度增加而增加,且发生红移．同样,数值模拟仿真结果表明电磁波的任何入射角对TE波都能产生大于305 nm的光波光子禁带,而TM波的光子禁带波宽随入射角增大会迅速减小．这就表明,用该结构制成的光波反射器对入射电磁波的极化较敏感．另外,该一维超导体光子晶体组成材料中,仅有超导体YBCO的相对介电常数会受外部温度的调节,不过由于其变化很小,也就是超导体YBCO的折射率随外部温度变化很小,因此仿真结果表明其反射率对外部温度的变化不明显．我们希望这些数值模拟仿真的结果能为设计可调的光波反射器提供理论研究基础．