同步误差条件下的空间目标双基地ISAR自聚焦算法
韩 宁,王立兵,郭宝锋,董 健,李宝晨
(1.军械技术研究所,石家庄 050000;2.中国人民解放军63961部队,北京 100012;3.陆军工程大学石家庄校区,石家庄 050003;4.陆军工程大学科研学术处,南京 210014)
0 引 言
与单基地逆向合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)相比,双基地ISAR成像过程不受目标运动方向限制,且具有良好的“四抗性能”,已逐渐成为雷达成像领域的研究热点[1-4]。国内外对双基地ISAR的研究主要集中在基本成像原理、成像平面确定、三维干涉成像中的微多普勒及越单元徙动补偿等方面[5-10]。
对于空间目标成像,双基地ISAR收发平台分置的配备方式会导致时间、空间及频率同步误差存在,同步误差必然会影响ISAR成像。就目前查阅到的文献而言,针对此问题的研究相对较少,一般的研究都是在三大同步理想可实现,不存在误差的假设条件下进行的[11-14]。
针对以上问题,本文以空间目标为研究对象,主要对同步误差对成像自聚焦的影响机理进行研究,将同步误差的影响用高阶多项式进行建模,然后估计高阶项系数构造补偿相位项完成初相校正。
1 双基地ISAR成像基本原理
空间目标双基地ISAR成像模型如图1所示。
图1中,Ci为目标上的散射点;Ei为该散射点在观测起始时刻于收发双站雷达和目标散射点中心构成的平面内的投影;Rr 0、Rt 0分别为收发双站在观测起始时刻相对目标散射中心的距离;RrCi 0、RtCi0分别为目标散射点Ci在观测起始时刻相对收发双站的距离;Rr 1、Rt 1分别为收发双站在目标运动到某一时刻相对目标散射中心的距离;Rv 0为目标相位中心的运动速度。
在较短的成像积累时间内,平稳目标在空间中的姿态是平稳的,为描述散射点在空间中的位置,建立以目标散射中心为原点的目标惯性坐标系,具体方法如下:以观测起始时刻目标双基地角平分线延长线方向为y轴正方向;以观测起始时刻目标轨道与目标双基地角平分线构成平面内y轴的法线作为x轴,x轴正方向与目标运动方向一致。该坐标轴指向不随目标的运动改变,因此该坐标系下目标散射点距离的变化包含目标的平动和相对转动。
为便于分析目标转动情况,建立目标的双基地角平分坐标系x′oy′,该坐标系的y′轴为双基地角平分线延长线方向,并随着目标的运动和双基角平分线指向的改变而改变;x′轴则是xoy平面内y′轴的法向。因此x′oy′坐标系与xoy坐标系间的相对转动角直接反映了目标在观测时间内的相对转动情况。
为便于后文论述,将本文研究的双基地ISAR二维成像基本流程简述如下:双基地ISAR成像雷达发射线性调频信号,对中频回波采样后通过正交双路零中频得到基频信号,然后在距离向通过脉冲压缩得到一维距离像,完成平动补偿后,方位向通过傅里叶变换得到二维IASR像。
假定双基地雷达理想同步,且雷达发射如式(1)所示的线性调频信号。
(1)
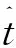
(2)
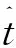
成像过程中,散射点的距离变化可表示为[12]:
(3)
式中:β0为目标成像期间的双基地角;Rref(tm)为成像过程中目标相位中心到收发双站的距离历程,可看成目标运动的平动距离项;2ricos(θCi+ψ(tm))cos(β0/2)为散射点Ci的转动距离项;ri为目标相位中心至散射点Ci的距离。从式(3)可以看出,对平动距离项补偿以后,进行距离向和方位向的压缩即可得到目标的双基地二维ISAR像[15-16]。
2 同步误差对双基地ISAR自聚焦的影响机理
分析
2.1 时间同步误差的影响
在双基地ISAR的接收站,因没有发射站的时间同步信号,故在接收站一般采用间接同步的连续采样模式完成中频信号采样,若目标满足“停-走模型”假设,通过连续采样模式采集中频回波并进行下变频后的目标散射点回波可表示为:
(4)
式中:
(5)
其中:τem为受时间同步误差影响的回波等效快时间位置;e(tm)是接收站与发射站之间的时间误差;φ0、φ1是常数相位项。
分析式(4)可以看出,式中的第一个相位项是带时移的线性调频项,匹配滤波后被消除;第三个相位项是固定相位项,与成像无关;第二项包含目标转动信息,与横向压缩有关,但该项不受时间误差的影响,与理想同步情况下的回波相位相同。因此,解决时间同步的间接同步连续采样模式对回波相位没有实质影响,不会影响横向压缩,也不会影响自聚焦。
2.2 频率同步误差的影响
若不存在频率同步误差,则散射点Ci的基频回波经脉冲压缩后可表示为:
(6)
式中:exp(-j2πf0RCi(tm)/c)包含了平动及成像所需的转动相位项,为分析方便,将该项用φtr表示,则φtr满足
(7)
一般情况下,频率同步误差Δf可按式(8)进行建模
Δf=ε0+ε1t+δF(t)
(8)
式中:ε0为误差的常数项偏置;ε1为误差的线性项系数;δF(t)为随机误差项。此时,式(7)应修订为式(9)所示形式
(9)
将RCi(tm)进行如下化简
=Rref(tm)-(2ricos(θCi)-2ri
(10)
式中:ω是成像期间双基地角的平均转动角速度,因成像时间较短,故近似认为是恒定速度。
(11)
式中:r0=a0-2yicos(β0/2),r1=b0+2xiωcos(β0/2),r2=c0。假设频率同步误差仅随慢时间变化,则将式(11)代入式(9)进行化简可得:
(12)
上式中忽略了随机相位项,且η0、η1、η2、η3满足如下关系
(13)
从式(12)可以看出,因为频率同步误差的存在,导致相位项出现了成像不需要的2次及3次高阶项。
2.3 空间同步误差的影响
双基地ISAR工作在跟踪状态且空间目标的运行轨道先验可知,因此,空间目标双基地ISAR的空间同步可基于先验可知的轨道数据进行跟踪引导而得到较好解决,故在分析时可认为不存在空间同步误差。
综合以上分析可以看出,在双基地ISAR的三大同步问题中,空间同步可以通过良好的轨道数据引导进行解决,时间同步也可通过间接同步的连续采样模式完成,而频率同步误差却造成了成像相位中的高次项,这必然造成图像的散焦。
在单基地ISAR中,针对以上问题主要采用时频分析的方法解决,但时频分析不能同时得到高的时间和频率分辨率,得到的是一系列动态成像序列,不利于对目标整体成像性能分析。本文研究提出一种基于高次项补偿的自聚焦方法。
3 基于高次项补偿的自聚焦方法
3.1 算法基本流程
成像期间,若脉冲重复周期用T表示,则tm=nT(n=0,1,…,N-1),式(12)可改写为
(14)
如式(14)所示,在存在同步误差的条件下,目标回波的相位项可表示为一个离散多项式相位信号(Polynomial Phase Signal,PPS)形式,若能估计出式(14)中的参数η2、η3,即可根据该参数构造补偿相位项完成回波的高阶相位补偿。
离散多项式相位变换(Discrete Polynomial-phase Transformation, DPT)是针对PPS的常用系数估计方法。
当用s(n)表示某个离散PPS,而利用DPT估计参数时,s(n)的表达式及符号算子DPM(M为正整数)分别定义如下:
(15)
DP1[s(n),τ]=s(n)
DP2[s(n),τ]=s(n)s(n-τ)
DP3[s(n),τ]=DP2[s(n)s(n-τ),τ]=
s(n)[s(n-τ)]2s(n-2τ)
⋮
DPM[s(n),τ]=DP2{DPM-1[s(n),τ],τ}
(16)
式(15)中,b0为多项式相位信号幅度;m为多项式相位信号阶数;am为第m阶系数;Δ为采样间隔。式(16)中,τ为延时长度。延时长度的选取会影响参数估计精度,对于此问题将在3.2小节进行论述。
另外一个重要的运算符为DPTM,PPS的M阶离散多项式相位变换DPTM定义为DPM[s(n),ω,τ]的离散傅里叶变换,可用式(17)表示如下
DPTM[s(n),ω,τ]=DFT{DPM[s(n),τ]}=
(17)
利用(16)、(17)估计出系数η2、η3,即可按照式(18)构造补偿相位项
φcom=exp(j2πη2(nT)2+j2πη3(nT)3)
(18)
将式(18)与式(14)相乘,即可得到成像所需的线性相位项。
基于以上分析,算法的基本步骤如下:
步骤1. 对于第一个距离单元,按照3.2小节的方法选取适当的延时参数τ1,计算DP3[s(n),τ1];
步骤2. 对DP3[s(n),τ1]进行离散傅里叶变换,利用式(19)估计三阶相位项系数η3;
(19)
步骤3. 对该距离单元数据乘上三阶补偿相位项,得到如式(20)所示的仅含二阶相位项的回波数据s2(n)
(20)
步骤4. 选取合适的延时参数τ2,计算DP2[s2(n),τ];
步骤5. 对DP2[s2(n),τ]进行离散傅里叶变换,利用式(21)估计二阶相位项系数η2;
(21)
步骤6. 对s2(n)乘上二阶补偿相位项,得到如式(22)所示的仅含线性相位项的回波数据s1(n)
(22)
以上仅针对某单一距离单元进行分析,对所有距离单元进行步骤1到步骤6的操作即可完成高阶转动相位项的补偿,最后在方位向进行傅里叶变换即可得到目标的二维ISAR像。
3.2 算法关键参数选择
在第2节的分析中,忽略了随机频率同步误差及3次以上高次项的影响。实际成像过程中,因目标的瞬时抖动、成像期间转动的短时非均匀等因素,不同距离单元的高次相位项阶数可能不一样,因此,在完成3.1小节的系数估计之前,需首先对各距离单元的相位项进行定阶。
若s(n)的阶数为M,则M阶PPS的DPTm具有以下特征,1)当m>M时,DPTm[s(n),τ]仅有直流成分;2)当m=M时,DPTm[s(n),τ]为非零频的单线谱,该单线谱的频率与第M阶系数有关;3)当m 延时参数τ1、τ2的选取会影响参数估计的精度,文献[17]对此问题进行了详细研究,假设信号长度为N,则当估计二阶及三阶相位系数η2、η3时,延时τ1、τ2分别选取N/2、N/3即能得到最高估计精度的参数。算法流程如图2所示。 图2中给出某一个距离单元的自聚焦算法流程,其他距离单元的处理流程与图2完全一致。如图2所示,算法首先估计三阶及二阶转动相位项的系数并完成三阶及二阶转动相位的补偿,当某个距离单元的转动相位项最高阶数仅为2阶时,可跳过3阶项系数的估计和补偿这一步,在图中用虚线表示。在完成高阶转动相位项的补偿之后,即可利用常规的非参数法自聚焦算法完成残余相位误差校正。 双基地雷达参数如表1所示,仿真时,用频域脉压的方法完成距离维成像,用累计最大互相关法完成包络对齐,自聚焦分别用相位梯度自聚焦(Phase Gradient Autofocusing, PGA)法和本文研究的方法进行,方位向压缩通过傅里叶变换完成,空间目标的初始两行轨道根数如表2所示,回波生成方法按照参考文献[18]的方法进行。仿真用目标的三维及对应的二维散射点模型分别如图3、图4所示。 表1 双基地雷达主要参数Table 1 Main parameters in bistatic radar 表2 初始轨道根数Table 2 Initial two line elements (TLE) 图5、图6、图7分别为用PGA算法、延时参数正常选取及延时参数有干扰项时的聚焦效果,从图中可以明显看出,当按3.2小节研究方法正确选取延时参数时,可得到比PGA算法更好的聚焦效果,但当延时参数选取不当时,其聚焦效果改善程度不如图6明显。 当延时参数τ1、τ2有干扰项,即τ1、τ2的选取不再是N/2、N/3时,待估系数η2、η3的最小方差与τ/N的关系大致呈浴盆曲线的形式[14],延时参数选取过小或过大,都会造成估计误差增长,而系数η2、η3的误差变大会导致补偿后的相位项依然存在残余高阶项,在后续的处理中,残余高阶项无法完全补偿,最终会造成图像聚焦度相对图6有所下降,如图7所示。 图8给出了η2、η3的估计精度随着成像时间的变化曲线,从图中可以看出,随着成像积累时间的变长,η2、η3的估计误差是逐渐降低的,但是,随着积累时间的增长双基地ISAR的图像畸变现象也会加剧,图9为成像积累时间等于15 s时的二维ISAR像,从图中可以看出,部分散射点的聚焦效果相对图6有一定改善,但因为图像的畸变,导致该二维ISAR像与目标的轮廓区别较大,不利于后续目标识别,故在利用本文研究的自聚焦方法时,成像时间一般选取10 s,以在参数估计精度和图像畸变之间选取合适的折中。 图像散射点的3dB主瓣宽度、积分旁瓣比(Integral Sidelobe Ratio, ISLR)和峰值旁瓣比(Peak Sidelobe Ratio, PSLR)常用于表征雷达成像性能,表3给出了多次仿真后统计平均得到的图5、图6、图7、图9的散射点参数性能。 从表3可以看出,在不同的成像算法条件下,散射点的距离向聚焦性能并未有明显提升,但方位向的聚焦性能改善明显,表明本文研究算法的有效性。从方位向的3 dB宽度、PSLR和ISLR来判断,图6的成像质量优于图9,图9的成像质量优于图7,这与前文的理论分析一致,因此若要利用本文方法得到高聚集质量的图像,必须按前文所述正确选取延时参数和成像积累时间。 表3 散射点参数性能Table 3 Imaging parameters of scatters 通过泰勒展开近似的方法,将频率同步误差与平动、转动的相位项统一进行多项式建模,通过估计高阶相位项系数的方法构造补偿相位项完成高阶项补偿,达成自聚焦的目的。算法在系数估计精度较高的条件下可得到比常用PGA算法更高的聚焦精度,但在估计参数选取不当时,对聚焦精度会有所影响。更加稳健的参数估计算法以及数据长度影响系数估计精度的机理分析也是课题组下一步的研究方向。4 算法仿真与分析



5 结 论

