基于数据选择的引信测试回波信号高精度延时

赵平伟，郭东敏，郑晨皓

(机电动态控制重点实验室，陕西 西安 710065)

0 引言

随着无线电引信工作体制及信号处理方法日趋复杂，对无线电引信测试系统功能及性能的要求也越来越高。实验室对调频多普勒体制无线电引信进行性能测试的核心技术是对引信发射信号的回波进行模拟，在该模拟过程中，回波信号相对于发射信号的延时精度决定了引信定距性能的测试精度，为了提高在测试过程中对引信定距精度的测量水平，就需要提高引信测试系统回波信号的延时精度。以往的无线电引信测试系统回波信号的延时方法主要包括光纤延时、仪器延时和基于现场可编程门阵列(FPGA)器件的延时。光纤延时的物理体积大[1]，而且延时时间的可变性不够好[2]，在进行高精度延时时，往往不是首选。仪器延时通过将信号输入仪器，在仪器中进行相关处理后输出进行延时，由于仪器自身本来就存在误差，加上仪器间的通讯等，导致引信测试系统回波信号的精度较低，一般在10 ns左右。由于FPGA延时是数字化的处理方式[3]，稳定性和可靠性高[4-6]，近年来被更多的人选择，文献[2]和文献[7]提出一种基于FPGA和FIFO的延时系统设计。FIFO是一种先进先出的数据存储器[8]，该方法实现的延时精度只能达到系统时钟周期，不能实现小于时钟周期的更高精度的延时；文献[9—10]都采用FPGA硬核输入/输出延迟单元(IODELAY)的方式实现延时，但它的使用与模数转换器(ADC)采样率有关，当ADC采样率较高时，IODELAY接收高速数据流，有可能在下一个边沿到来时，还没有完成对上一个边沿内的数据处理，致使数据出错，不适用于引信测试系统回波信号的高精度延时。针对实验室无线电引信测试系统回波信号延时精度低的问题，本文基于FPGA平台，提出通过数据存储和数据选择方式来实现引信测试系统回波信号高精度延时。

1 基于FPGA的无线电引信测试系统回波模拟原理

1.1 基于FPGA的引信测试回波模拟系统

基于FPGA的引信测试回波模拟系统采用基于数字射频存储(DRFM)的硬件平台[11]，由上下变频器、高速模数转换器(ADC)、高速数模转换器(DAC)、控制器、存储器、同步时钟以及本振信号等单元组成，如图1所示，文献[12]论证了将DRFM技术用于无线电引信信号处理的可行性。在引信测试回波模拟系统中，引信测试系统回波信号的延时处理由控制器中的延时单元进行实现。

首先，将接收到的射频信号下变频为中频信号。由于采样器件的制约，现在的DRFM尚不能对射频信号进行直接处理，而是需要把射频信号下变频到中频频段。下变频就是根据射频信号频率去调谐本振，从而使下变频器的输出在中频频段内。其次进行模/数转换。对射频下变频之后的中频信号进行采样，将模拟信号转换为离散的数字信号序列，实现中频信号的数字化。再次，进行信号存储。采集完成之后的数字信号，进行中频下变频成为基带信号序列，将其存储在存储器中，由控制器实现对该信号的延迟、多普勒平移及幅度变化模拟等相关处理操作。再进行数模变换。对数字信号序列完成中频上变频的信号处理后，通过DAC将数字信号转变成为模拟信号，从而实现中频信号的输出。最后进行射频信号重构。上变频DAC转换得到的模拟信号，使用下变频共用本振，将中频信号混频得到射频信号，从而实现射频信号输出。

1.2 无线电引信测试系统回波信号延时原理

基于FPGA的引信回波模拟系统首先将截获的引信发射信号经过下变频和低通滤波得到中频信号，再经过数字下变频得到基带信号后，对其进行延时和相关处理。设引信发射信号为St,up(t)，本地振荡器产生的信号为L(t)，M(t)为下变频后经低通滤波后的中频信号。

(1)

L(t)=A1cos(2πfLt+φL)

(2)

(3)

M(t)=ALcos(πμt2+ω1t+φM)

(4)

对其进行中频数字化采样，采样间隔为Ts，则时域离散信号表示为：

M(n)=AL(n)cos{[πμ(nTs)2+ω1nTs+φM]}

n=1,2,3,…

(5)

经过数字正交混频技术，可得到该中频信号的同相与正交分量I(n)、Q(n)，其中I(n)、Q(n)分别表示为：

(6)

(7)

该基带信号经数字存储延时时间为τ，其中τ=NTs，N为延时周期个数，每周期为Ts，则经存储延时后表示为：

(8)

(9)

完成延时后，对该信号进行数字同相正交上变频，得到：

M′(n)=I′(n)cos(ω1(n-N)Ts)+Q′(n)sin(ω1(n-N)Ts)=

(10)

将该信号由数模转换器转换为模拟信号为：

(11)

最后通过上变频器件将频谱搬移至发射信号中心频谱f0处：

(12)

与式(1)对比，即完成了时间τ的延时(幅度变化不影响延时精度，本文只关注信号的相对延时)。

2 基于数据选择的引信测试系统回波信号高精度延时

为了实现引信测试系统回波信号的高精度延时，将延时单元分为粗延时单元和精延时单元两部分，原理框图如下图2所示。

图2 延时单元原理框图Fig.2 Principle block diagram of time delay unit

经ADC处理后的引信信号进入延时单元后，首先进行粗延时，再进行精延时。粗延时单元主要是将时钟周期整数倍的时间通过存储进行延时，精延时单元主要是将小于时钟周期的时间通过数据选择进行高精度延时。

在实现引信测试系统回波信号高精度延时的过程中，需要通过自行编写算法来实现粗延时单元中的存储延时功能和精延时单元中的数据选择功能，具体实现过程将通过“粗延时单元”和“精延时单元”两部分分别进行介绍。

2.1 粗延时单元

粗延时单元通过编写的算法控制双口随机存取存储器(RAM)来实现，通过算法中的读写控制来实现对信号的存储延时。流程图如图3所示。

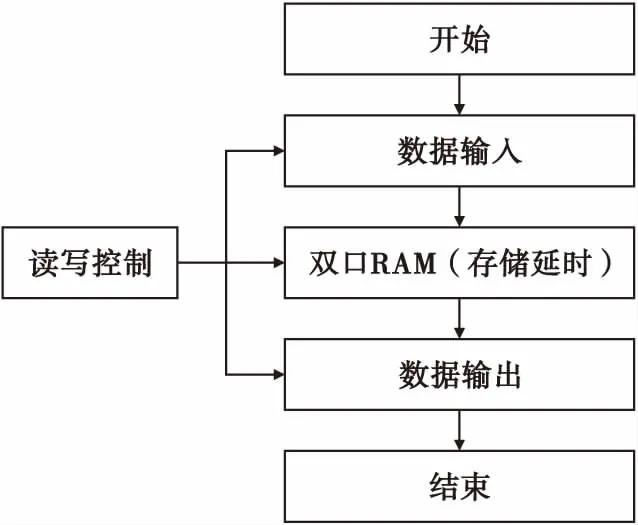
图3 粗延时单元流程图Fig.3 Coarse delay unit flow chart

粗延时单元工作原理如式(13)所示：

延时时间(T) = 时钟周期(T0) × 周期个数(N)

(13)

式(13)中，时钟周期T0是指粗延时的同步时钟，从上式可以看出，总的延时时间是时钟周期的整数倍，即粗延时的基本延时精度最高能达到时钟周期T0。粗延时模块主要将时钟周期的整数倍时间进行延时，小于周期数的时间由精延时模块实现。本设计选择的kcu105平台时钟周期为4 ns，即粗延时的延时精度为4 ns。

2.2 精延时单元

精延时单元通过编写的算法控制数据选择的方式来实现。由于本设计选择的kcu105平台时钟周期为4 ns，为了实现精度为1 ns的延时单元设计，故将输入信号分为四路，根据小于时钟周期的精延时时间量，对四路数据进行选择输出，

假设将输入信号分为A0、B0、C0、D0四路，用A1、B1、C1分别表示对A0、B0、C0延迟了一个时钟周期，O1、O2、O3、O4表示输出，精延时单元流程图如图4所示。

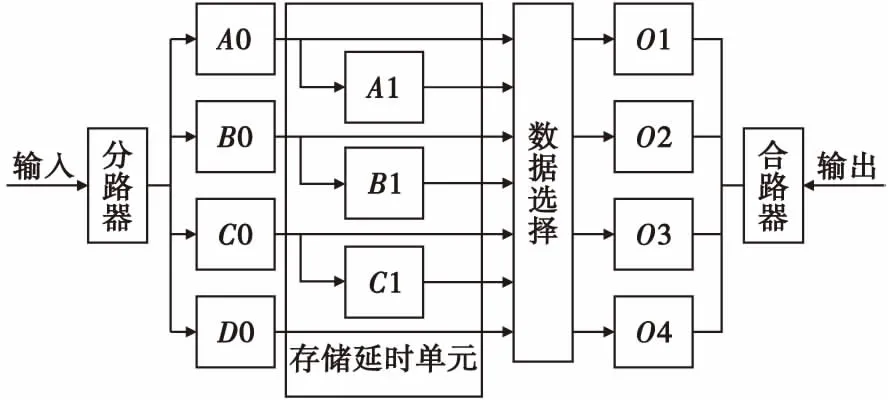
图4 精延时单元流程图Fig.4 Fine delay unit flow chart

其中数据选择模块的行为可用下表1描述。

表1 数据选择模块行为描述Tab.1 Description of data selection behavior

由以上可得，当延时为0 ns时，输出A0、B0、C0、

D0；当延时为1 ns时，输出B0、C0、D0、A1；当延时为2 ns时，输出C0、D0、A1、B1；当延时为3 ns时，输出D0、A1、B1、C1。以此来实现小于时钟周期的延时。

3 实验验证

本实验验证选择的是赛灵思(Xilinx)公司的kcu105平台，时钟周期为250 MHz，系统精度为4 ns；AD，DA选择的是AD-FMCDAQ2-EBZ套件，其中包括AD9680和AD9144。AD9680是一款双通道、14位、1 GSPS模数转换器(ADC)。AD9144是一款四通道、16位、最高采样率达到2.8 GSPS的数模转换器(DAC)。

粗延时的延时范围与存储器的容量有关，例如，本设计的引信测试系统回波信号周期为2 000 ns，延时范围不会超过两个周期，即不会超过4 096 ns的最大延迟量，所以需要的存储器存储深度为1 024，本设计输入1路数据，位宽为64 bit，总数据量为1 024×1×64=64 KB，该实验平台的存储量为2 GB，完全满足需求。

实验采用Vivado 2015.4软件进行原理设计，设计结果如下图5所示。

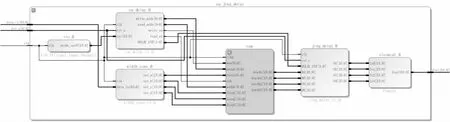
图5 模块整体设计Fig.5 The overall module design

其中，VIO_0模块提供延时控制量；cu_delay_0模块为读写控制模块；输入信号在ram模块中进行粗延时，在jing_delay_0模块中进行精延时；width_conv_0模块为分路器，xlconcat_0模块为合路器。设计完成后将该设计下载到KCU105开发板进行实验验证。

3.1 粗延时单元实验验证

本实验的系统时钟周期为4 ns，所以粗延时可以对4的整数倍的时间进行延时，输入信号周期为2 000 ns。由于普通的引信测试系统回波模拟器器件固有延时大于引信测试系统回波信号所需要的延时，所以在引信测试系统回波模拟过程中需要跨周期处理，此处对信号分别进行2 100 ns和2 600 ns的延时，结果如图6和图7所示(从示波器上可以读出相对延时的Δ值)。

2 100 ns和2 600 ns都是时钟周期4 ns的倍数，对其进行存储延时即可得到图6和图7的结果。由以上实验结果可知，该方法能够满足引信测试系统回波信号粗延时需求。

图6 2100 ns粗延时Fig.6 Coarse Delay of 2100ns

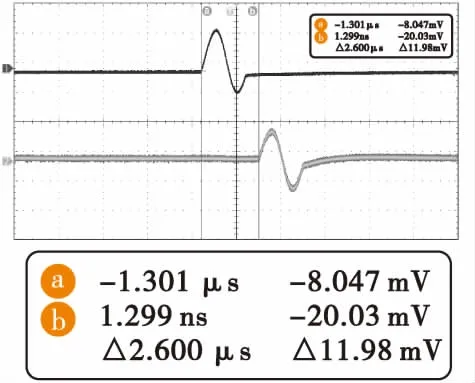
图7 2 600 ns粗延时Fig.7 Coarse Delay of 2 600 ns

3.2 精延时单元实验验证

本实验将精延时精度由4 ns提升到了1 ns，即精延时模块可以对4以内的整数进行延时，达到1 ns、2 ns和3 ns的物理实现。此处为了让实验结果在示波器上显示的更加清楚，实验分别对输入信号进行600 ns、601 ns、602 ns、603 ns的延时，上述数据除以4后的商由粗延时模块实现，余数分别为0、1、2、3，由精延时模块实现，延时后的结果如图图8—图11所示。

图8 600 ns精延时Fig.8 Fine Delay of 600 ns

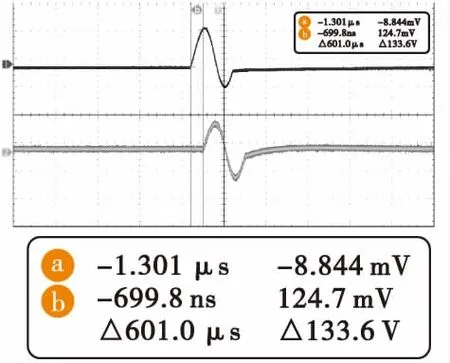
图9 601 ns精延时Fig.9 Fine Delay of 601 ns

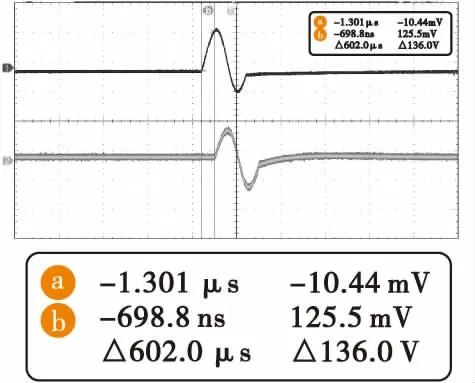
图10 602 ns精延时Fig.10 Fine Delay of 602 ns

图11 603 ns精延时Fig.11 Fine Delay of 603 ns

从示波器上可以看到，信号的延时是以1 ns为递进的，即延时精度达到了1 ns。

在此需要特别说明的是，由于精延时精度为1 ns，示波器在捕获数据时需要将示波器的标度放大到1 ns甚至更高精度进行数据的捕获。本实验首先将示波器标度放大后进行数据捕获，由于标度放大后波形无法辨别，故在捕获完数据后恢复标度，而捕获数据保持不变。

由以上实验结果可知，本文提出的基于FPGA的引信测试系统回波信号高精度延时方法中的粗延时单元设计方案能够满足引信回波模拟过程延时需求；精延时单元设计方案能够将延时精度由时钟周期的4 ns提升到1 ns。

4 结论

本文基于FPGA平台，提出通过数据存储和数据选择方式来实现引信测试系统回波信号高精度延时，该方法利用自行编写的算法控制粗延时单元中的数据存储和精延时单元中的数据选择方式进行实现，使得在满足延时要求的基础上，有效提高了引信测试系统回波信号的延时精度。实验结果表明本文提出的粗延时单元设计方案能够满足引信测试系统回波信号的延时需求，精延时单元设计方案能够将延时精度从FPGA时钟周期的4 ns提升到1 ns，意味着无线电引信定距测试精度从0.6 m提升到0.15 m，测试精度提升到了一个更高的水平。