杂波未知条件下基于箱粒子滤波的CBMeMBer算法

董 青，胡建旺，吉 兵，张 浩

(1.陆军工程大学石家庄校区信息工程系，河北 石家庄 050003；2.陆军西安军事代表局驻兰州和乌鲁木齐地区军代室，陕西 西安 710043)

0 引言

传统的基于数据关联[1]的多目标跟踪算法会带来组合爆炸问题，在复杂电磁环境中，由于存在大量虚警、杂波，该环境下，数据关联算法的跟踪性能急剧下降。基于随机有限集[2](Random Finite Set，RFS)的多目标跟踪技术近年来发展迅速，其特点在于将目标状态和观测分别用有限集的形式表示，避免了显式数据关联，大大降低算法复杂度。Mahler先提出基于一阶矩近似的概率假设密度[3](Probability Hypothesis Density，PHD)滤波算法；在PHD基础上提出基于势近似的CPHD[4]。2008年Mahler提出基于多伯努利随机集的多目标多伯努利[5](Multi-Target Multi-Bernoulli，MeMBer)跟踪算法，但该算法存在数目过估的问题。Vo在文献[5]的基础上进一步提出势均衡多目标多伯努利[6](Cardinality balanced MeMBer，CBMeMBer)滤波算法，解决了原始MeMBer算法目标数过估的问题，并给出了CBMeMBer滤波算法的高斯混合实现形式。

在真实跟踪场景下，由于电磁环境、温度和其他因素影响，杂波密度、检测概率、量测噪声概率分布等先验知识都难以准确获取。不精确的先验知识会造成跟踪出现误跟、漏跟等情况，造成跟踪算法性能不理想。针对检测概率和杂波密度未知场景下的目标跟踪问题，文献[7]提出了基于CBMeMBer的鲁棒性算法，但该算法在检测概率较低场景下性能不佳。在此基础上，文献[8]提出使用代价函数去选择传感器，提高了目标个数和状态的跟踪精度，但运算复杂度较高，仅适用于目标个数较少的跟踪场景。

由于粒子滤波是通过一组在状态空间里传播的随机样本近似概率密度函数，粒子数越多，近似程度越高，同时运算量也越高。为解决这一问题，文献[9]将区间分析理论与粒子滤波结合，提出了箱粒子滤波(BPF)。文献[10—11]提出基于箱粒子滤波的CBMeMBer(Box-CBMeMBer)滤波算法，与SMC-CBMeMBer算法相比，在跟踪精度相近的条件下，上述文献所提算法的运行时间和粒子数目都远小于SMC-CBMeMBer算法，但需要较理想的跟踪环境。针对杂波未知环境，文献[12—13]分别提出了基于箱粒子滤波的PHD算法和LMB算法。

经上述分析可知，在未知杂波条件下，传统的CBMeMBer算法无法保证较好的跟踪精度，且需要庞大的粒子集而致使跟踪效率低下。本文针对此问题，引入区间分析理论，提出了杂波未知条件下基于箱粒子滤波的CBMeMBer算法(RCBMeMBer)。

1 杂波未知条件下的跟踪问题描述

研究杂波未知条件下的多目标跟踪问题，关键在于如何区分杂波和目标。因此考虑在杂波未知环境下将目标状态空间进行扩展，表示为混合状态空间[14]，用以传递目标状态和杂波状态两种信息。

1.1 空间模型的建立

定义混合状态空间的数学表达式为：

χ=X⊕λ

(1)

式(1)中，χ表示混合状态空间，X表示运动状态空间，⊕表示并集，λ表示杂波空间。为方便描述，引入标号u，取值为0或1，当u=1时，表示该函数或取值与目标相关，反之，当u=0时，表示函数或取值与杂波相关。

1.2 杂波未知条件下的CBMeMBer算法

1)预测

设k-1时刻的多目标密度为：

(2)

则k时刻预测的多目标密度为：

(3)

(4)

(5)

2)更新

已知k时刻预测的多目标密度为：

(6)

则其k时刻更新的多目标密度可近似表示为：

(7)

其中，

(8)

(9)

(10)

(11)

(12)

(13)

φu,k,zk(x)=gu,k(z|x)pD,u,k(x)

(14)

pD,u=1,k(x)为传感器的目标检测概率，pD,u=0,k(x)为杂波检测概率，gk(·|x)为单目标状态似然，κk(zk)为杂波强度。

2 基于箱粒子滤波的CBMeMBer算法

由于R-CBMeMBer算法在进行目标跟踪时，需要大量的粒子近似后验概率密度，导致算法复杂度较高。本文将箱粒子滤波思想引入到杂波未知的跟踪环境中，提出基于区间分析的R-CBMeMBer滤波算法，以提高杂波未知环境下的R-CBMeMBer算法执行速度。

1)初始化

(15)

2)预测

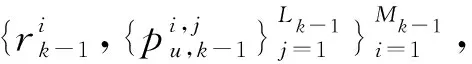
(16)

(17)

假设轨迹的存在概率为：

(18)

存活目标的概率密度为：

(19)

(20)

(21)

之后对存活目标权值和新生目标权值进行归一化。

3)更新

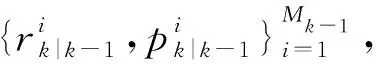
(22)

更新后的粒子后验分布可计算如下：

(23)

(24)

(25)

(26)

(27)

(28)

(29)

其中，

(30)

(31)

(32)

(33)

(34)

(35)

(36)

4)约束箱粒子

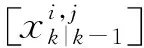
(37)

5)轨迹修剪

与标准SMC-CBMeMBer类似，随着时间的增加，表示后验概率密度的粒子数目会出现无限增长的趋势，为降低计算复杂度，我们需设置轨迹门限，将存在概率小于门限值的轨迹进行剔除。

6)重采样

基于箱粒子滤波的CBMeMBer在滤波过程中也会出现粒子退化现象，为减轻粒子退化对滤波效果的影响，需对修剪后的假设轨迹的粒子进行重采样，重采样方法与粒子滤波类似。

7)目标状态提取

首先累加假设轨迹存在概率即可得到目标数目估计，计算目标状态均值，分别提取目标状态和杂波状态。

3 仿真实验

为验证算法的有效性，将SMC-CBMeMBer算法、R-CBMeMBer算法与本文改进算法进行对比。

3.1 仿真场景设置

本文仿真场景设置为：仿真时间为100 s，仿真步长为1 s，观测区域为x-y二维平面区域[-2π,2π]*[0,2 000 m]。监测区域先后出现六个做转弯运动(CT)的目标。状态方程为：

xk=Fxk-1+wk

(38)

其中，σ1,w=5 m/s2，σ2,w=π/180 rad/s2。

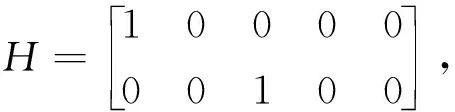
3.2 算法性能分析

为验证算法有效性，本文采用最优子模式分配(OSPA)[15]距离作为新算法评价准则，其中距离敏感性参数p=3，截断距离c=100。在CBMeMBer的序贯蒙特卡罗和箱粒子实现中粒子个数分别为1 000和40，新生粒子数分别为300和1。在监测区域内，最多有六个目标出现，监视步长T=1，监视周期为100 s。图1为目标的运动轨迹图。

图1 真实运动轨迹图Fig.1 True track trajectory

本文设置两种仿真场景，仿真场景一(低杂波密度)：杂波模型先验已知λ先验=λ实际=10；仿真场景二(高杂波密度)：杂波模型与先验模型不匹配且λ先验=10，λ实际=50。

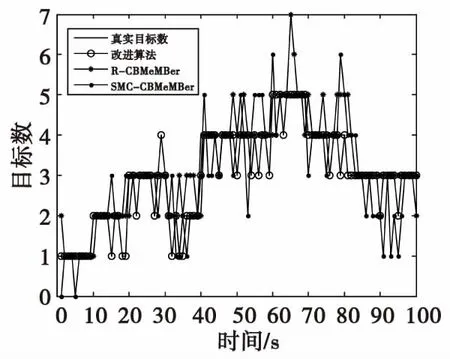
图2 低杂波密度条件下目标数估计值Fig.2 Target number estimation under low clutter density condition

图3 高杂波密度条件下目标数估计值Fig.3 Target number estimation under high clutter density condition

图2、图3分别展示了三种算法在标准条件和杂波先验未知条件下的目标数目估计结果。由图可以看出，41个箱粒子能力等效于1 300个标准粒子的能力。本文所提改进算法在低、高密度条件下均能较好的估计目标数目。经过100次蒙特卡罗仿真，表1给出了三种算法目标数平均估计结果，验证了改进算法的势估计性能高于其他两种算法。

表1 三种算法数目估计正确率对比图

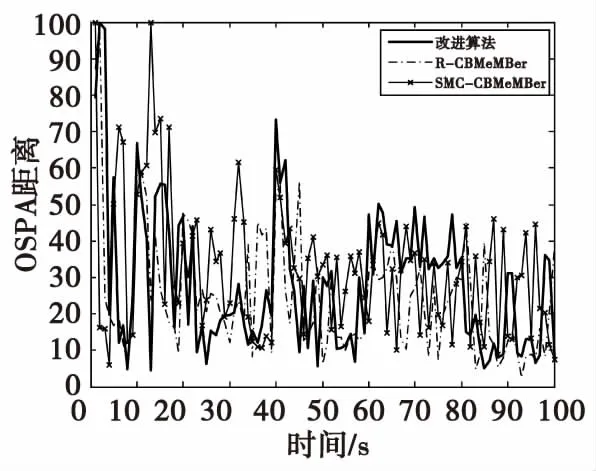
图4 低杂波密度条件下OSPA距离Fig.4 OSPA distance under low clutter density condition

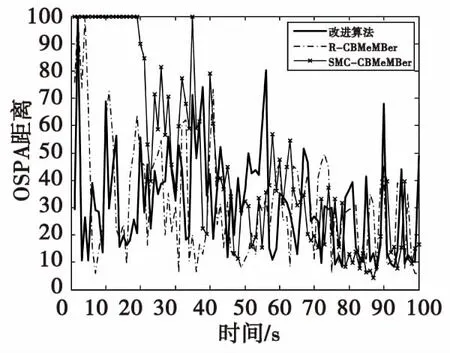
图5 高杂波密度条件下的OSPA距离Fig.5 OSPA distance under high clutter density condition

图4给出了低杂波密度且先验已知条件下三种算法的OSPA距离，可知SMC-CBMeMBer算法的跟踪误差较大且不稳定，改进算法的跟踪性能与R-CBMeMBer算法相近；图5对比了三种算法在高杂波密度先验未知条件下的OSPA距离，由于杂波先验模型与真实杂波模型不匹配，SMC-CBMeMBer算法的OSPA距离远高于改进算法和R-CBMeMBer。表2给出了三种算法的OSPA距离对比图，在低杂波密度且先验已知条件下，改进算法的性能最好，R-CBMeMBer算法次之，SMC-CBMeMBer算法最差。在高杂波密度且先验未知条件下，改进算法的OSPA距离远小于标准SMC-CBMeMBer算法。

表2 三种算法OSPA距离对比图

由上述仿真实验可知，改进算法的算法性能略高于R-CBMeMBer算法，表3对比了三种算法的运行时间，改进算法的运行时间不到R-CBMeMBer算法的十分之一，在高杂波密度条件下，改进算法在保持跟踪性能的前提下，算法的执行速度得到显著提高。

表3 三种算法运行时间对比图

4 结论

本文提出了杂波未知条件下基于像例子滤波的CBMeMBer算法。该算法在R-CBMeMBer算法的基础上 引入箱粒子滤波思想，修正混合状态空间预测、更新方程，使用箱粒子代替传统粒子传递后验概率密度。仿真结果表明，在杂波先验已知或未知条件下，改进算法在保证跟踪精度的同时，又大幅度缩减了算法执行时间，具有较高的工程应用性。但本文所完成的是普通条件下的多目标跟踪，没有考虑目标机动时如何处理。因此，将交互式多模型(IMM)和本文所提算法相结合是解决未知杂波密度条件下机动目标跟踪的一个方向。