敏捷成像卫星调度的改进量子遗传算法
王海蛟,贺 欢,杨 震
(1. 中国科学院大学,北京 100190;2. 中国科学院国家空间科学中心,北京 100190)
0 引 言
成像卫星调度问题的本质是为成像卫星选取观测任务,指定观测时间。相比于传统成像卫星,敏捷成像卫星增加了俯仰和偏航两个自由度,这使敏捷成像卫星具备更强的对地观测能力。然而,这也使得敏捷成像卫星调度问题的解空间变大,且管控中敏捷成像卫星的观测开始时间是一个具有连续值域的变量,非敏捷卫星调度所采用的组合优化的调度方法不再适用[1]。
国内外许多学者都就敏捷成像卫星调度问题进行了研究:Lema Tre[2]研究了单颗敏捷卫星调度中的任务选择问题,在只考虑单圈轨道的敏捷成像卫星调度问题的情况下,建立简化模型,并提出贪婪算法、动态规划、约束满足、局部搜索四种不同的算法。Habet[3]等对禁忌搜索算法进行改进,采用一致性渗透的采样方法来加搜索空间,同时,引入局部穷举搜索算法,提高算法的优化结果。Sun[4]等针对敏捷卫星成像调度问题,提出一种改进的遗传算法,显著提升了调度效果。Hao[5]等建立一种考虑任务消耗、任务完成率、应用效益的多目标敏捷成像卫星调度模型,并提出一种结合蚁群算法(ACO)和遗传算法(GA)的杂合算法。刘嵩[6]等就敏捷成像卫星自主规划问题进行研究,采用建立卫星动作序列模版方式,设计多种启发式规则建立一种单星自主规划模型。Geng[7]等建立了一种二进制与整数变量混存的调度模型,并提出一种二进制与整数杂合编码的遗传算法求解敏捷成像卫星调度问题,并结合一个启发式规则选取观测开始时间。郝会成[8]等基于诚信机制的可解约合同网任务分配方法,设计了招投标机制和评标策略等,提出一种Multi-Agent敏捷卫星任务规划调度方法。Zang[9]等提出了一种改进的遗传算法,通过高质量初始解快速的生成敏捷成像卫星的规划方案。王建江[10]等引入非约束支配路径的概念,提出基于标记更新思想的动态路径搜索算法(DPSA)对成像卫星调度问题进行求解,DPSA算法在牺牲一定求解效率的基础上,能够提高调度效果。严珍珍[11]等人将均匀设计思想引入蚁群算法设计,提出一种改进的蚁群算法,目的在于解决蚁群算法参数设计难的问题。孙凯[12]等针对敏捷卫星对地观测中直拍直传、立体成像等复杂任务需求以及成像观测、数据下传、对日定向等九种卫星动作,设计了基于专家知识的多种启发式规则,用于决定任务安排并同时安排卫星动作序列。
这些研究大都将敏捷成像卫星调度抽象为考虑能源、存储、时序等约束的优化问题。模型的决策变量多采用单一整数或者二进制数。然而,单一决策变量常常导致在求解算法中编码长度过长,影响求解效率。同时,二进制与整数的决策变量也难以有效表达敏捷成像卫星解空间连续问题。就求解算法而言,现有研究多采用智能优化算法和启发式算法,这些算法有的采用二进制或者整数编码,如遗传算法;有的采用实数编码,如蚁群算法;而采用混合编码的研究还较为少见。
量子遗传算法是目前应用较为广泛的一种量子优化算法,相比于传统智能优化算法具有很好的寻优和收敛性能。量子遗传算法在量子空间进行寻优搜索的特性也可以很好解决连续搜索问题[15]。
本文针对敏捷成像卫星调度问题中解空间大,解空间离散与连续并存的难题,提出一种多种决策变量混合的敏捷成像卫星调度模型;与经典卫星调度模型不同,多种决策变量混合的调度模型将任务的接受与否,任务时间窗口选择,任务观测开始时间选择分别用不同决策变量进行表征,可以更好描述敏捷卫星调度问题。以此为基础,本文提出一种二进制与实数杂合编码的改进量子遗传算法;杂合编码可以有效表达敏捷成像卫星离散与连续并存的解空间。此外,杂合编码的二进制部分与实数部分在寻优过程中并行搜索,有助于提高算法效率和求解质量。同时,由于量子优化算法的量子叠加态可以提高种群多样性,使得改进的量子遗传算法具有优良的寻优和收敛性能,可以快速有效求解敏捷成像卫星调度问题。
1 多决策变量的敏捷成像卫星调度模型
1.1 问题分析
相比于传统成像卫星,敏捷成像卫星多了俯仰和偏航两个自由度,使得任务的可用时间窗口变多,且时间窗口变长。相比于一般的成像调度问题,除选定任务的时间窗口,还需在选定时间窗口内选择具体的观测时间,使敏捷成像卫星的调度具有更大难度。如图1所示,对于非敏捷成像卫星而言,仅能在特定的时间观测目标,而敏捷成像卫星对目标的观测时间则可以在[t1,t2]这样一个连续时段中选择。
大部分现有研究多以整数或者二进制决策变量来对该问题进行建模,客观上会把敏捷成像卫星调度问题的解空间离散化,不同的离散化粒度对搜索求解质量有很大的影响(如图2中(a),时间窗口0被离散化为开始时间是t0,t1,t2的三个时间窗口)。若直接采用连续变量进行表征,又会复杂化问题,降低求解效率(如图2中(a),直接采用观测时间To作为决策变量,在连续时间域上进行搜索)。
针对以上敏捷成像卫星调度问题的特性,本文将敏捷卫星成像调度的问题描述为由两个离散域搜索和一个连续域搜索并存的优化问题,具体描述如下:
给定可用敏捷成像卫星集合和待完成的任务集合,每个任务具有多个通过过境分析等预处理获得时间窗口,形成任务的时间窗口集合。敏捷成像卫星调度是在满足卫星使用约束的前提下,从任务集合选定一组待观测任务(离散域搜索);然后为这些选定的任务从其时间窗口集合选择一个时间窗口(离散域搜索),并从所选时间窗口中指定任务开始观测时间(连续域搜索);调度目标是最大化卫星的应用效益,本文选取完成任务优先级之和作为卫星应用效益的度量值。通过分开描述任务选择和任务观测时间确定,避免了时间窗口在问题建模阶段的离散化,从而使得模型和搜索算法能更好覆盖敏捷成像问题的解空间。
1.2 数学模型
1.2.1符号定义
为描述方便,首先给出以下符号定义:
(1)观测任务
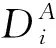
(2)敏捷成像卫星
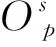
(3)时间窗口
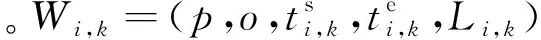
(1)
其中,rα是t时刻的横滚角度,φα是t时刻的俯仰角度;该序列可用Satellite Tool Kit (STK)在时间窗口预处理阶段获得。
(4)决策变量及其值域
与一般敏捷成像卫星调度模型不同,本文采取多决策变量描述敏捷成像卫星调度中的决策,定义如下:
任务选择决策变量xi:xi=1表示第i个任务被选择,xi=0表示不选择。
时间窗口选择决策变量yi:yi表示给第i个任务选择的时间窗口的序号;若yi=k则安排任务在第k个时间窗口Wi,k上执行。
成像时间决策变量ti:ti代表第i个任务的开始观测时间。
1.2.2敏捷成像卫星调度的问题模型
基于上述分析与定义,敏捷成像卫星调度问题可以转换为带约束的多变量混合优化问题,问题求解就是找出一组决策变量集合,并满足以下条件:
(2)
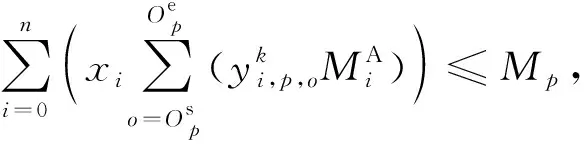
(3)
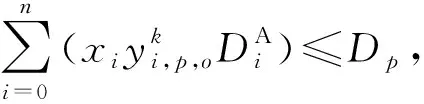
(4)
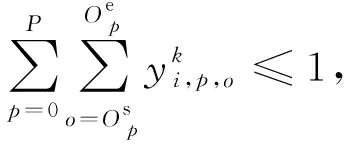
(5)
ti+di+ftran(p,i,j)≤tj
(6)
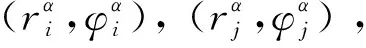
(7)

与一般的卫星调度模型不同,本文所建立的调度模型中,分别采用二进制、整数、实数三种决策变量来表达敏捷成像卫星调度中关于任务选择、时间窗口选择、成像时间选择这三种不同值域的决策,更好表达了敏捷成像卫星调度问题。此外,基于该模型,在本文第三节所提出的改进的量子遗传算法中,可以用一位编码表达一个任务的所有时间窗口,简化了编码结构;同时无需进行任务唯一执行的约束检查(式(5)),使算法在以该模型为基础进行搜索时,避开一部分不可行解,提高搜索效率。
但该模型中二进制决策变量xi、整数决策变量yi、实数决策变量ti并存,是一个复杂的复合变量规划问题,常见的成像卫星调度求解算法难以适应。因此,本文提出一种改进的量子遗传算法用以求解敏捷成像卫星调度问题。
2 改进的量子遗传算法
常见的智能优化算法有PSO,遗传算法,差分进化等,这些算法各有优劣,如PSO和差分进化高效但易限于局部最优,遗传算法收敛速度较慢等。
2.1 量子遗传算法简介
Han[14]等基于量子比特和量子叠加态概念,结合遗传算法提出一种量子遗传算法,由于量子系统可以表达叠加态,从而一条量子状态的染色体可以描述多种系统状态,相比于传统遗传算法,使量子遗传算法具有更好的种群多样性和收敛性。一个双态量子位的状态可以表示为:
|r=α|0+β|1
(8)
式中:α和β分别代表|0和|1的量子态概率幅,它们满足归一化条件:
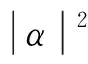
(9)
目前常见的量子遗传算法大多采用量子比特幅的量子态编码结构,如式:
(10)
对应的实体染色体编码一般采用二进制编码结构[16],如式(11):
s=(b0,…,bi,…,bm),bi∈{0,1}
(11)
实体染色体基因位取值一般通过观测函数计算得出,观测函数形如式(12):
bi=f(αi,βi)
(12)
与传统遗传算法不同,量子遗传算法的搜索寻优是在相位空间中利用量子门更新量子位概率幅实现。

量子遗传算法基本流程如图4所示:
量子遗传算法虽然具有很好的性能和特性,但目前大多数量子遗传算法采用基于量子位测量的二进制编码方式或实数编码方式,存在解码复杂等问题。基于量子位测量的二进制编码方式或实数编码方式也不能有效适应本文所提出的多种决策变量混合的敏捷成像卫星调度模型。因此,本文提出一种二进制与实数混合的杂合编码;以杂合编码为基础,将多决策变量的敏捷成像卫星调度模型的解空间映射到量子空间中,从而引入量子遗传算法求解敏捷成像卫星调度离散与连续并存的优化问题。
2.2 改进的量子遗传算法
针对敏捷成像卫星调度问题,本文对量子遗传算法进行以下适应性改进:提出二进制与实数编码相结合的染色体编码方式,将敏捷成像卫星的解空间映射到相位空间;杂合编码的二进制编码部分和实数编码部分在相位空间分别更新,由不同观测函数测量并解码生成敏捷卫星调度模型中的决策变量,实现连续域与离散域的并行搜索;同时,采用混沌序列、量子旋转门和量子非门相结合的方式进行种群更新。
2.2.1杂合染色体编码
如第1节中所述,敏捷成像卫星调度问题中的决策分为三部分:第一,任务是否选择执行;第二,若任务被选择执行,则从其时间窗口选择一个时间窗口;第三,在选择的时间窗口中选择开始观测时间。n个任务的观测方案可以表示为:
V={(x0,y0,t0),…,(xi,yi,ti),…,(xn,yn,tn)}
(13)
式中:xi,yi,ti分别是第二节中多决策变量调度模型中关于观测任务选择,时间窗口选择和成像时间选择的决策变量。
本文提出一种二进制与实数杂合的染色体编码方式对敏捷成像卫星的调度方案进行编码,编码方法如式所示:
X={(b0,u0),…,(bi,ui),…,(bn,un)}
(14)

(15)
ui=yi+zi,yi∈{0,1,…,m},zi∈[0,1]
(16)
式中:X代表一个成像方案的杂合染色体编码。(bi,ui)代表第i个任务的染色体编码。ui是一个实数,它的整数部分代表任务时间窗口选择,小数部分代表观测时间在所选时间窗口内部的滑动比例。m是第i个任务时间窗口数目。杂合染色体的解码策略在2.2.2节给出。
图5为一个杂合编码染色体的示例,图中染色体所代表的含义为任务0拒绝;任务1接受,观测安排在任务1的第1个时间窗口,开始时间为第1个时间窗口开始时间延迟20%窗口时长;任务2接受,观测安排在第1个时间窗口,开始时间为第1个时间窗口开始时间延迟30%窗口时长。
杂合染色体的编码长度仅和任务数目有关,不随卫星数目和时间窗口数目增多而增长,有助于在卫星数目多时提高算法效率。相比于二进制或者整数的编码方法,杂合染色体的编码结构简单,解码容易。
2.2.2杂合编码的量子概率幅编码及观测函数
在量子遗传算法中,染色体的进化是在量子空间中进行。杂合染色体的量子位概率幅编码与杂合染色体相对应,分为两部分:
A.染色体二进制编码的量子概率幅编码
染色体二进制编码的量子概率幅定义如式(17):
(17)
对应的观测函数如式(18),α0为选定的阈值,本文中选定α0=0.5:
(18)
任务选择决策变量由杂合染色体二进制部分解码得出:xi=bi。
B.染色体实数部分的量子概率幅编码
染色体实数部分的量子概率幅编码定义如式(19):
(19)
对应的观测函数如式(20):
(20)
式中:m是第i个任务时间窗口数目。
时间窗口选择决策变量的取值是杂合染色体实数部分的整数部分,计算方法如式(21):
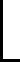
(21)
成像时间决策变量计算方法如式(22)和式(23):
zi=ui-yi
(22)
(23)
2.2.3基于量子旋转门和量子非门的个体更新
量子遗传算法通过量子门更新染色体基因位的量子概率幅更新种群。本文选取量子旋转门和量子非门进行种群更新,考虑交叉算子需要个体之间进行交叉拷贝,会降低算法的运行效率,本文没有选取交叉算子。
A.基于混沌序列的量子旋转门个体更新
利用量子旋转门对染色体第i个基因位的更新如式所示:
(24)
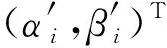
(25)
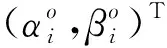
本文通过混沌序列确定转角大小。利用混沌遍历性对每个基因位设置不同的转角,可引入随机性增加种群多样性,降低早熟可能。转角大小计算方法如式(26):
(26)
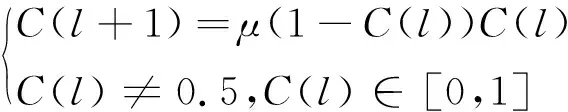
(27)
式中:l为待更新染色体在种群排序,N为种群规模,μ为混沌系数,本文取μ=4, Δθ0=0.0785。显然,对于排序越靠前的染色体,其转角Δθi会受限变小,从而减小种群退化的可能。
B.基于量子非门的个体更新
在基于量子旋转门的种群更新中,各染色体依靠当前最优染色体引导进行更新,若当前最优染色体是一个局部最优解,就可能导致早熟现象。为增强种群的多样性,减小早熟的可能,考虑到量子非门无需当前最优染色体的介入,本文同时采用量子非门对种群进行扰动更新。具体而言,就是依据变异概率随机选择数条染色体,然后随机选取选中染色体的部分基因位,对这些基因位施加量子非门操作。量子非门更新公式定义如式(28)所示
(28)

2.2.4约束检查与收益计算
约束检查时,按照时序约束式(6),成像时长约束式(4),存储约束式(3)的顺序逐个检查每个观测任务安排的可行性;当有任务冲突时,优先退出低优先级的任务。卫星的应用效益是所有可行任务的优先级之和,计算方法如式(29):
(29)
2.2.5改进的量子遗传算法流程
基于以上设计与改进,本文将量子遗传算法引入敏捷成像卫星调度问题中。改进的量子遗传算法的流程如图6所示:
3 仿真校验与结果分析
本节通过仿真对多决策变量的敏捷成像卫星调度模型的有效性和改进的量子遗传算法的优越性进行校验。
3.1 仿真设定
仿真采用的计算机的配置为酷瑞i7, intel双核处理器,主频 2.4 GHz,内存为4 G,操作系统为windows 7,编程环境为pyhon3.5。由于卫星调度领域还没有公认的任务测试集合,因此本文设计了一个可以依据不同输入生成不同规模调度问题的生成器。问题生成器可以通过输入不同的空间范围和时间范围,生成观测任务目标序列。为描述方便,本文在后续仿真试验中将m颗卫星n个任务的问题记为m×n。仿真参数见表1。

表1 仿真参数Table1 Parameters of Simulations
任务的观测目标为在输入空间范围内随机产生的点目标,任务的成像要求时长在3~5 s之间,任务优先级在1~10之间。卫星星载存储器的最大容量设为240 G,瞬时视场角度设为3°,最大俯仰角度35°,最大侧摆角度45°,姿态稳定时间为10 s,俯仰机动角速度为3(°)/s,侧摆机动角速度为3(°)/s。
3.2 仿真结果分析
为测试本文所提出的杂合编码的量子遗传算法在敏捷卫星调度问题中的性能,本文做了6组不同规模的仿真(4×100, 4×200, 4×300, 5×100, 5×200, 5×300),并与基于杂合编码的遗传算法(HGA)和二进制编码的遗传算法(GA)[9],量子遗传算法(QGA)[14],蚁群算法(ACO)[11]的运行结果进行对比。其中HGA的编码方式和解码策略采用本文所提出的杂合编码方法。所有算法的姿态转换时间均采用本文的方法计算。每组仿真共运行10次,选取总收益和运行耗时的平均值作为评估指标。仿真中算法所用的参数见表2。仿真结果见表3,表4。

表2 量子遗传算法/遗传算法参数Table 2 Parameters of QGA, HGA and GA
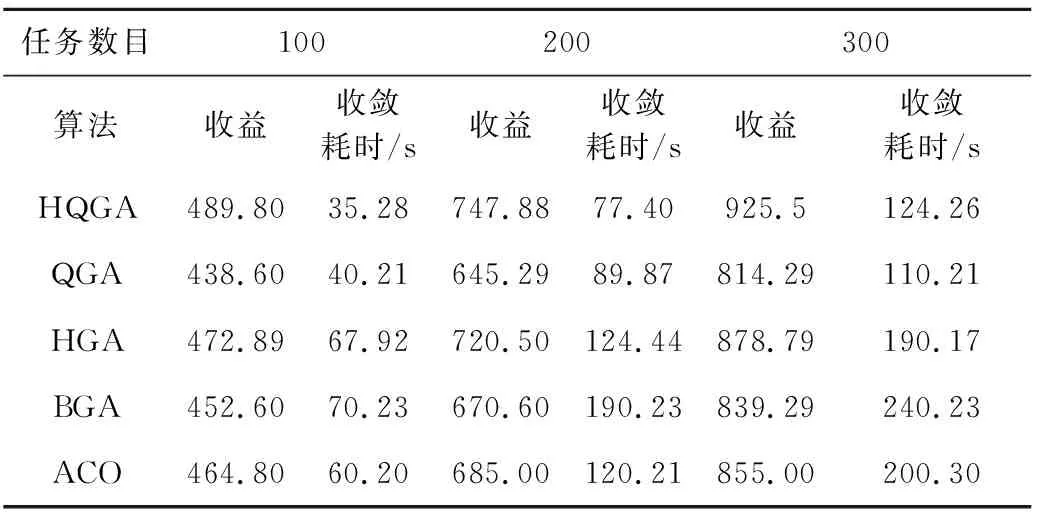
表3 算法调度结果对比(卫星数目:4)Table 3 Performance comparison (Satellites: 4)

表4 算法调度结果对比(卫星数目:5)Table 4 Performance comparison (Satellites: 5)
从表3,表4中可以看出,在相同的问题规模下,HQGA获得的收益最高,耗时最少。HGA和BGA相比具有更高收益和更低的时间消耗,这说明在相同的搜索机制下,采用杂合编码有利于提高求解质量和运行效率。对比HQGA和HGA,采用量子优化机制的HQGA比HGA的收益更高,说明引入量子优化机制的有效性。同时,HQGA无需交叉操作,免去了一部分交叉拷贝带来的时间消耗。
进一步分析可以看出在HQGA在相同任务规模下的耗时大致相同(4×100规模下35.28 s, 5×100规模下36.02 s, 4×200规模下77.40 s, 5×200规模下79.62 s),类似的现象也出现在HGA的仿真结果上,这是因为卫星数目的上升会增加可用的时间窗口,加长二进制编码长度,从而增加解码时间消耗。而本文提出的杂合编码长度仅和任务数目相关,卫星数目的上升不会对算法运行造成影响。
综上所述,本文所提出的基于杂合编码改进的、量子遗传算法在敏捷成像卫星调度这种解空间离散与连续并存的优化问题上具有很好寻优和收敛性能,可以有效解决敏捷成像卫星调度问题。
4 结 论
本文针对敏捷成像卫星调度中面临的解空间大、离散搜索与连续搜索并存的问题,提出一种基于杂合编码的改进量子遗传算法(HQGA)。杂合编码具有编码长度短,解码简单等优势;同时,基于量子优化机制,杂合编码的二进制部分与实数部分可以在量子空间独立并行更新,从而提高算法的寻优与收敛性能。仿真试验结果表明,基于杂合编码的量子遗传算法可以有效解决敏捷成像卫星调度问题。

