基于意图推断的高超声速滑翔目标贝叶斯轨迹预测
张 凯,熊家军,李 凡,付婷婷
(1. 空军预警学院研究生管理大队,武汉 430019;2. 空军预警学院四系,武汉 430019)
0 引 言
作为新一代跨大气层空天飞行器,以HTV-2、AHW为代表的高超声速滑翔目标(Hypersonic Gliding Reentry Vehicle, HGRV)结合航天器与航空器的特征,能利用其高升阻比外形机动形成一个较大的打击区域[1-2]。与传统惯性目标相比,其轨迹预测的可能性大大降低,这给拦截防御带来巨大挑战。针对HGRV这类机动不确定目标的轨迹预测问题,采用传统弹道预测方法难以准确预测,需结合目标的运动和作战特点寻求新思路[3]。
现有的HGRV轨迹预测方法大多是从目标历史飞行数据出发,根据量测数据辨识出目标的气动力参数[4-5]、速度倾角[6]、控制变量[7]等参数,结合初始估计状态积分外推实现轨迹预测。对于防御方而言,这类不考虑目标未来机动的轨迹预测方法能预测的时间窗口十分有限,无法满足防御作战需求。虽然HGRV轨迹预测面临极大困难,但由于目标在高超声速条件下机动能力受热防护、气动布局、制导控制规律等约束,其机动特征并非完全无章可循[8]。此外,在对空中目标态势与威胁评估中,通过推断目标的飞行意图可以有效降低未来机动不确定性的影响,这种基于意图推断的轨迹预测思路在机器人行为推测[9-10]、民航轨迹预测[11-12]和飞航导弹拦截[13-14]等领域上得到广泛认可,具有一定借鉴意义。
据以上分析不难看出,针对HGRV机动不确定问题,结合目标运动特点合理推断飞行意图是提高长期轨迹预测准确性的有效途径之一。为此,本文首先对HGRV进行动力学建模,利用气动参数构建HGRV的机动模式集。然后在假定来袭HGRV必定攻击某目标的前提条件下,结合其飞行意图合理构造代价函数,利用贝叶斯原理迭代推导机动模式和运动状态的递推公式,最后通过蒙特卡洛采样实现贝叶斯轨迹预测算法。期望通过这种基于意图推断的贝叶斯轨迹预测思想为HGRV长期轨迹预测提供一定理论指导。
1 问题描述
从图1中可以看出,状态估计反映了目标当前飞行状态,推断的意图反映了目标飞行目的,仅利用状态外推或者飞行意图对HGRV这类机动再入目标进行轨迹预测都会降低预测精度。本文所提轨迹预测方法旨在结合两者优势,这种基于意图推断的思路需要解决两个问题:一是利用动力学模型构建HGRV机动模式集,覆盖目标在未来时刻可能的飞行样式;二是结合飞行意图推断目标的机动模式,利用机动模式对应的预测模型对HGRV进行轨迹预测。下文内容分别从这两点出发进行阐述。
2 预测模型
机动不确定条件下的HGRV轨迹预测依赖于机动模式集的构建。传统飞航式目标一般利用不同转弯率表示转弯模型表示相应的机动模式,由于HGRV的机动能力往往受到特定环境、技术因素限制,难以实现类似飞航式目标的复杂机动。因此,HGRV机动模式集应当根据其运动特性设计,保证预测的轨迹可飞。本节在动力学建模基础上,结合目标机动特点,构建HGRV的机动模式集。
2.1 动力学模型
未知量气动加速度a的改变是造成HGRV机动的主要原因。对于HGRV这类机动再入目标的动力学建模问题,比较流行的做法是将气动加速度a从雷达站东北天(East-North-Up, ENU)坐标系转换到半速度(Velocity-Turn-Climb, VTC)坐标系中,表示成含气动参数u=[αv,αt,αc]T的表达式[15]:
(1)
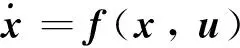
(2)
式中:r为目标瞬时地心距;B为雷达站地理纬度;Re为地球半径。
2.2 机动模式集
飞行器机动模式由控制规律决定。HGRV控制参数包括攻角α和倾侧角υ,攻角α主要作用是维持目标稳定飞行,通常取为常值或变化较小;倾侧角υ是实现机动飞行的主要控制参数,通过改变升力方向实现预期的机动动作,表现为爬升力参数αc和转弯力参数αt的变化[16]。
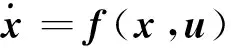
已知气动参数u与控制变量的关系式为[15]:
(3)
式中:CD(α)、CL(α)分别为阻力系数和升力系数,与攻角α有关;S为目标等效截面积,m为目标质量,均为常值。对于防御方而言,上述参数与控制变量均为未知量。
再入滑翔过程中,由于攻角α变化较小,且主要影响纵向运动,为减小构建机动模式集的复杂度,可忽略攻角α对机动模式的影响,利用不同倾侧角υ对应的气动参数u表示HGRV在相应机动模式下的机动输入。受到目标气动特性的限制,υ的变化范围通常可取为-40~40度,在没有先验信息的条件下可假设υ取值符合正态分布。为此,在轨迹预测过程中,需要解决气动参数u的预测问题。为避免υ变化对气动参数u预测的不利影响,定义升力参数αl:
(4)
结合式(3)~(4)可知,αv和αl是CD(α)和CL(α)的函数,与倾侧角υ无关。研究表明CD(α)和CL(α)随攻角α近似线性变化[17],因此,对αv和αl进行预测从而间接得到气动参数u的思路是比较合理的。具体步骤:
(1) 参数估计 根据量测数据利用动力学模型(2)估计出气动参数u=[αv,αt,αc]T,通过式(4)计算αl的估计值,并对估计值进行平滑处理。
(2) 参数预测 可采用以下两种方法拟合αv和αl变化规律:①时间序列分析方法:采用(p,d,q)阶ARIMA模型[18];②最小二乘法:构造拟合多项式[5]。
(3) 机动建模 根据不同机动模式下倾侧角υ取值,结合式(3)~(4)计算相应气动参数u的预测值。
3 贝叶斯轨迹预测
基于意图推断的轨迹预测是根据实时战场态势进行轨迹规划过程:首先是从量测数据中提取出对意图推断有用的信息,然后按照推理机制对预测轨迹进行规划。实质是根据飞行意图对目标未来状态进行估计的问题,即推断未来某时刻目标在特定空域内概率大小的问题。贝叶斯估计能够有效地利用已经获得的先验知识,用概率的形式描述目标的运动状态[8,10]。本节在构造意图代价函数的基础上,利用贝叶斯理论迭代预测HGRV的机动模式和运动状态。
3.1 意图代价函数
决定HGRV作战意图的主要因素有航向误差角、弹目距离以及目标重要度[19]。同时,HGRV应避免进入一些特定的区域,如反导系统拦截区域、易受敌探测或电磁干扰、地缘政治因素不允许通过的区域。综合考虑以上因素,定义HGRV意图代价函数为:
g(θη|x)exp(-a·σ(x,θη)+b·d(x,θη))·
(5)
式中,θη∈Θ表示打击目标,φκ∈Φ表示避飞区;d(·)为弹目距离,σ(·)为航向误差角;a、b分别表示各因素权重系数;Iθ(·)表示打击目标的重要度;Iφ(x,φκ)表示φκ对代价函数的影响,定义为:
Iφ(x,φκ)
(6)
式中:c·dmin(x,φκ)表示危险区半径,参数c>1为安全裕度。Iφ(x,φκ)表示当HGRV距离φκ较远,不考虑避飞区影响;当HGRV进入危险区,d(x,φκ)越小,则Iφ(x,φκ)越小,代价越大。下面给出dmin(x,φκ)计算方法。
如图2所示,令a=1,当HGRV恰好可以以最小转弯半径r从避飞区边缘飞过,此时目标与避飞区中心O的距离d(x,φκ)定义为dmin(x,φκ)。根据三角形正弦定理可知:
(7)
式中:HGRV瞬时最小转弯半径r可根据状态x估算[8]。根据式(7)可求出dmin(x,φκ)。
3.2 状态外推理论
通常认为HGRV会沿代价函数减小的空域飞行。因此,可根据代价函数g(θη|x)定义机动模式j下状态转移概率分布:
p(xi|xi-1,uj)K-1·g(θη|xi)-1
(8)
式中归一化系数K为:
(9)
为以一种迭代方式计算目标状态的后验概率密度函数,计算过程分为模式推断和状态外推。对于模式推断,首先根据状态分布p(xi+1|x1:i)以及模式的先验概率p(uj|x1:i-1)推断模式的后验概率:
(10)
根据模式概率Pr(uj|x1:i)对目标状态进行一步外推:
(11)
依据这种思路通过递推方式更新机动模式和目标状态的后验概率,状态的k步外推公式如下:
(12)
3.3 蒙特卡洛算法
由于模式概率p(uj|xi)为非高斯分布,同时,状态转移函数p(xi|xi-1,uj)为非线性的动力学模型,系统通过贝叶斯递推获得的状态后验概率函数p(xi+1|x1:i)无法得到显式解。作为一种适合于非线性非高斯系统的递归贝叶斯滤波方法,蒙特卡洛序贯滤波(粒子滤波)可以利用粒子采样模拟空间中目标状态的后验概率密度函数,近似计算目标在空间中概率分布[20]。蒙特卡洛算法的基本步骤如下:
(1) 步骤一 数据准备
1) 根据量测数据得到估计值X0,根据αv和αl预测值构造机动模式集U;
2) 参照文献[21]方法估计HGRV的再入覆盖范围,确定可能打击的目标θη∈Θ;
(2) 步骤二 模式推断
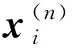
(3) 步骤三 状态外推
3) 根据式(8)和(9)计算粒子概率。
依据这种思路对粒子状态进行更新和采样,从而近似得到目标状态的概率分布。这种基于粒子概率的描述形式解决了空间中状态难以积分运算的问题,提高了算法的适用性。
4 仿真校验
为验证方法可行性,设计以下仿真环境:1) 飞行器参数:HGRV模型参考美国洛马公司CAV-H的基本参数[22],采用三自由度动力学方程积分弹道[16],目标初始速度为4000 m/s,初始高度40 km,攻角随速度线性变化;2) 量测参数:定义相控阵雷达采样间隔为0.1 s,距离量测标准差为500 m,方位角、俯仰角量测标准差均为0.01 rad;3) 算法参数:预测时间约为340 s,气动参数采用ARIMA模型进行时间序列预测,机动模式个数为5,预测粒子个数为50;3)仿真场景:HGRV意图攻击某目标,采用标准制导法[16]控制倾侧角实现机动转弯并避免飞入特定区域,飞行时间约为500 s。
实验1 单目标轨迹预测
图3~4表示HGRV气动参数的估计与预测结果。不难看出,虽然目标发生了机动转弯,但αv和αl总体上呈近似线性变化,未发生剧烈波动,这是因为αv和αl与倾侧角变化无关。气动参数预测RMSE随时间逐渐增大,但均比预测值小一个量级,在允许范围内。可见,根据对气动参数估计值训练ARIMA模型对气动参数的预测可以较好地逼近真实值,有助于提高轨迹预测准确度。
图5表示HGRV轨迹的跟踪与预测粒子散布结果。可以看出,为避免进入避飞区,HGRV不断改变机动模式飞行。在已知打击目标的情况下,粒子集根据飞行意图进行轨迹预测,当某些粒子距离打击目标较远,或者预测粒子进入避飞区,通过代价函数计算的粒子权重逐渐减小,而权重大的粒子数量通过重采样后大幅增加,从而优化预测轨迹规划结果。
为对比验证本文所述方法的有效性,分别采用四种方法对HGRV进行轨迹预测:1) 文献[4]基于升阻比变化规律的方法;2) 文献[5]基于气动参数变化规律的方法;3) 本文所提方法,但不考虑避飞区;4) 本文所提方法,考虑避飞区。图6表示四种方法对比示意图,其仿真时间分别为:0.24 s、0.27 s、12.83 s、11.75 s。分析上述结果不难发现:1) 方法一中升阻比变化规律未考虑转弯机动,仅对目标纵向状态进行外推,预测偏差较大;2) 方法二通过气动参数变化规律辨识目标的机动模式,其轨迹在预测初期与HGRV运动趋势基本保持一致,当目标改变机动模式后,由于未考虑飞行意图,预测误差迅速发散;3) 方法三和方法四考虑了HGRV的飞行意图,预测得到的轨迹与目标运动趋势基本保持一致,虽然预测偏差逐渐增大,但未发生发散。同时,由于方法四考虑了避飞区信息,其预测轨迹更加接近于真实轨迹。4) 从仿真时间来看,本文方法计算复杂度显著高于传统算法,这是由于蒙特卡洛方法需要不断寻优最佳机动模式,相对于长达数百秒的预测轨迹时效而言,仿真时间能够满足拦截需求。
实验2 多目标轨迹预测当HGRV再入覆盖范围内存在多个可能打击目标时,根据方法可以得到多条预测轨迹。为识别HGRV的真实飞行意图,利用意图代价函数计算各目标的概率,进行目标威胁排序。仿真结果如图7-8所示,分别表示多目标轨迹预测和意图推断示意图。
从图7中可以看出,当t=0 s时,根据算法无法预测意图为目标1的轨迹,可排除;当t=150 s时,同理可排除目标4;当t=300 s时,对于目标2和3均可以得到预测轨迹,此时应同时考虑对两个目标的威胁。从图8中可以看出,当时间为0~150 s时,判定目标4威胁最大;随着HGRV机动转弯,同理依次判定目标1、目标2威胁最大。
以上仿真结果表明,对于单目标情况,本文方法能够有效降低目标未来时刻机动不确定对轨迹预测的不利影响。同时,本文方法仅能够在一定程度上反映目标真实的运动趋势,无法精确预测轨迹。对于多目标的情况,算法可能存在打击目标误判,但随着跟踪时间增加,识别准确性会大幅提高。为避免误判,当多目标概率相差不大时,应同时考虑多条预测轨迹,以降低误判带来的风险。
5 结 论
在研究HGRV长期轨迹预测过程中,目标机动是难以回避的问题。本文在传统状态外推预测思路的基础上,提出基于意图推断的贝叶斯轨迹预测方法。方法根据贝叶斯理论迭代求解了HGRV的运动状态和机动模式,利用蒙特卡洛采样近似计算了HGRV的概率分布,避免了复杂空域概率密度积分困难。
仿真对比表明,由于升力参数和阻力参数变化较小,利用ARIMA模型对其进行参数预测取得了预期效果。相对传统方法,结合意图推断的轨迹预测方法有助于减小目标未知机动对轨迹预测的不利影响。对于多目标的情况,应同时考虑其打击的可能性,降低误判带来的风险。

