非合作空间目标自主交会凸优化制导技术
池贤彬,许 琦,李之强,岳晓奎
(1. 湖北航天技术研究院总体设计所,武汉 430040;2. 西北工业大学航天学院,西安 710000)
0 引 言
非合作空间目标是指在空间交会接近操作(Rendezvous and Proximity Operations, RPOs)中,该类目标不受控制,且往往具有不稳定机动、自旋和章动等运动状态。追踪航天器和非合作目标无法保持稳定的相对状态,这对RPOs的姿态和轨迹规划、制导和控制过程带来巨大困难。
针对空间非合作目标的自主交会接近技术具有广阔的应用前景,如:空间碎片及小行星的探索任务;失效航天器在轨维护任务;空间拦截与对抗任务。面向非合作目标的典型航天任务包括NASA的“深度撞击”彗星撞击任务与ESA的“罗塞塔(Rosetta)”彗星登陆探测计划等。其中,罗塞塔卫星于2014年11月12日,释放登陆器“菲莱(Philae)”,对67P彗星实施软着陆。但受彗星自旋和复杂地形的影响,以及受制于罗塞塔卫星缺乏高效的针对非合作空间目标的自主交会技术,特别是不具备实时接近轨迹规划与制导能力,导致着陆点位于一个悬崖下方,使登陆器菲莱的太阳帆板光照条件较差,电源供应不足,严重影响了探测计划的实施效果。可见,当前的航天任务迫切地需要一种面向非合作空间目标的自主交会技术,尤其是在线轨迹规划与制导方法。
现有针对RPOs问题的轨迹规划方法主要包括以极小值原理[1]为基础的间接法;基于参数优化的伪谱法[2];遗传算法(GA)[3]、粒子群算法[4]等大规模全局随机搜索算法等。以上方法都能成功地完成轨迹规划和制导,但仍然存在一些不足:1)不适应面向非合作空间目标的交会任务要求;2)部分方法实时性和鲁棒性较差,大多属于事先规划和开环制导;3)大多方法不能严格保证全局最优性和收敛性,或对初始猜测值和终端条件很敏感。
为满足针对非合作空间目标的自主交会技术应用需求,经过大量的前期工作,本文认为,基于凸优化的制导技术拥有计算高效、鲁棒性良好的特点,具备工程应用前景。
凸优化是目前众多寻优方法中在实时性和最优性方面表现最为突出的算法,尤其是在人们重新界定原始对偶内点法[5]的应用后,大大减少了计算耗时。Behcet A[6]研究了凸优化方法在火星软着陆轨迹规划的问题,利用无损凸化技术将原始问题转化为标准的二次序列凸优化问题(Sequential quadratic Convex Programming, SOCP),并严谨地证明了凸化过程的等价性和收敛性,奠定了凸优化方法在航天应用领域的理论基础。随后,Liu Xing-fu等[7]研究了基于凸优化的远程自主交会问题;Wang Z B、林晓辉和刘延杰等[8]则对行星再入、小天体附着、与月面着陆的轨迹优化问题进行凸优化应用研究;罗建军等[11]对凸优化方法在仅测角交会制导的应用开展了研究。
现有针对RPOs的研究大多都忽略了非合作空间目标的运动特性,或者将其简化,假设其拥有恒定的(角)速度,在交会时间已知的前提下,通过预测末端状态,将动态特性转化为较易处理的末端约束,该方法仅适用于动态特性较小的非合作交会任务。本文在凸优化理论的基础上,对面向非合作空间目标的六自由度自主交会的数学模型进行凸化处理,同时考虑推力、内点状态等约束;重点分析目标规避机动、自旋和章动等动态特性造成的制导误差,并设计了制导修正策略;基于某飞行器姿轨控系统,提出了一种基于凸优化算法的制导方案,将凸优化方法从一种事先规划算法发展为一种在线制导算法;并对非合作目标机动、自旋和章动情况下的自主交会任务进行数值仿真,校验了该方法的可行性,论证了凸优化方法的工程应用价值。
1 问题描述
1.1 自主交会接近任务描述
自主交会接近技术是指两个空间飞行目标于同一时间在轨道同一位置以相同速度会合的技术,是空间组装、在轨服务、卫星捕获等大量新概念航天任务的基石。参与交会的两个空间目标中,不可控且不配合交会任务的一方,称为非合作目标(航天器),如失效卫星、小行星、空间碎片等;而主动执行一系列机动,飞向目标航天器的一方,称为追踪航天器,如飞船、航天飞机等,如图1所示。
1.2 坐标系定义
本文涉及的相关坐标系包括:
1)Sto:轨道坐标系T-XtoYtoZto,原点在目标航天器质心T,Xto与目标航天器位置矢量rt同向,Yto轴在轨道面内与Xto垂直且指向速度方向,Zto轴满足右手定则,如图1所示。为了描述非合作目标航天器的动态特性,定义初始时刻轨道坐标系Sto-0:T0-XtoYtoZto,其原点在初始时刻的目标航天器质心T0,其他各个轴的定义同Sto。
2)Stb:目标航天器本体坐标系T-XtbYtbZtb,原点在追踪航天器质心T,Xtb、Ytb、Ztb分别与惯性主轴重合,如图1所示。
3)Scb:追踪航天器本体坐标系C-XcbYcbZcb,原点在追踪航天器质心C,Xcb、Ycb、Zcb分别与惯性主轴重合,如图1所示。
1.3 控制方案与推进系统配置
某追踪航天器控制系统方案如图2所示。通过激光与视觉相对导航系统,测量追踪航天器与目标航天器的相对轨道和相对姿态信息;经凸优化制导算法和PID控制算法解算出连续的三轴推力和力矩;随后利用脉宽脉频调制(PWPF)技术,得到推进系统控制指令;最后由推进系统产生推力和力矩,执行姿态和轨道控制,实现自主交会接近。其中交会接近轨迹控制参考坐标系为目标航天器轨道坐标系,追踪航天器的姿态控制参考坐标系为目标航天器本体系。
该追踪航天器的主要执行机构是一套姿轨控一体推进系统,推进系统包含四个四向一体喷管,具体构型与配置方案如图3所示,推力器组合使用方式如表1所示,每个推力器额定推力为5 N。
由表1可知,姿控通道与轨控通道存在一定耦合,这对制导算法和控制算法的鲁棒性提出了更高的要求。表中的推力和力矩是在追踪航天器本体系中描述的,而制导算法解算出的控制量则是在目标轨道坐标系描述,在控制指令执行时需要进行坐标系转换,将目标轨道坐标系的控制指令转换至追踪航天器本体系。

表1 某追踪航天器推力器组合使用方式Table 1 Thrusters combination mothed method
2 数学建模与分析
2.1 相对轨道动力学模型
假设航天器是任意轨道上的一个质点,只考虑控制力,利用在Sto坐标系下的T-H方程描述椭圆轨道上的航天器相对运动。
(1)
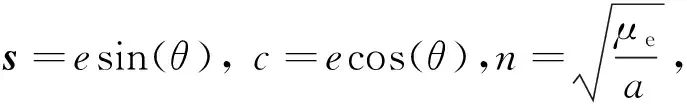
式中,μe为地球引力常数;目标航天器轨道平均角速度为n,轨道偏心率为e,半长轴为a;x,y,z是追踪航天器在Sto坐标系下的三维位置状态;m是追踪航天器的质量;U是追踪航天器的推力控制矢量;rt是目标航天器地心矢量的范数;θ是目标航天器真近点角;νe是发动机喷气速度,为已知常数;xr0是初始相对位置,为已知量。
考虑追踪航天器在接近过程中由于燃料消耗引起的质量变化,定义质量变化函数
(2)
以接近轨迹最省能量为优化目标,同时考虑内点约束与安全接近约束,定义如下:
(3)
(4)
Cf(tf)xr(tf)+Df(tf)=0
(5)
C0(t0)xr(t0)+D0(t0)=0
(6)
E[xr(t)]+F(t)≤0
(7)
式中,t0是交会任务的起始时间,tf是终端时间,均为已知量。线性等式(5)表示终端相对位置约束,线性等式(6)表示初始相对位置约束,均为一个凸约束;不等式(7)表示安全接近角约束,采用线性不等式形式:
(8)
线性不等式(8)是一个严格线性凸约束。式中α、β分别是Ytb和Ztb方向的半锥角,均为已知量。
2.2 追踪航天器姿态动力学模型
假设航天器是一个刚体,在追踪航天器本体坐标系Scb下,只考虑控制力矩的情况,使用线性化的欧拉角方程描述姿态运动。
(9)
模型是一个线性时不变系统,一个凸约束,具有较为简单的形式,常用于描述小角度机动的姿态运动。
以最省能量为优化指标,考虑力矩上限、内点约束和终端约束。
(10)
(11)
Mf(tf)xa(tf)+Nf(tf)=0
(12)
M0(t0)xa(t0)+N0(t0)=0
(13)
M[xa(t)]+H(t)≤0
(14)
式(12)、(13)是始、末姿态约束,式(14)是姿态角约束,均为凸集。
2.3 问题的离散化处理
式(2)表示交会过程中追踪航天器质量变化状态,由于质量m是一个时变量,这导致了动力学模型(1)的非线性,在本文中则做如下处理,令
(15)
式中:下标k表示迭代制导周期次数序列,Δmk-1表示第k-1制导周期的质量消耗。上式表明在每一个迭代制导周期内的追踪航天器质量不变。
T-H方程是一组时变线性方程组,拥有较高精度和简洁的形式,适用于任意轨道和任意距离下的RPOs问题。将式(1)离散化,其状态转移矩阵取状态矩阵的一阶近似,离散化后的形式为:
(16)
式中,i∈{1,2,…,tf/Δt}, Δt是离散时间步长,Φr是运动方程的状态转移矩阵,Gr是轨道控制矩阵,上式是一个线性的凸约束,I是单位矩阵。
姿态方程(9)是一个线性时不变系统,可以很容易得到其离散形式:
(17)
式中,Γ是拉普拉斯变换符号,Φa是姿态方程的状态转移矩阵,Ga是姿态控制矩阵,上式也是一个线性的凸约束。
式(7)表示为避免碰撞而给定的安全走廊约束,离散化后表达式为
Ei[Xr(i)]+Fi(i)≤0
(18)
式(14)表示姿态约束,离散化形式为:
Mi[xa(i)]+Hi(i)≤0
(19)
式(4)和(11)表示推力和力矩的约束,凸化的离散形式为:
(20)
离散化后的性能指标为:
(21)
经过以上处理过程,可以定义离散的凸优化问题,用于描述六自由度的RPOs问题。
目标函数:
约束条件:
{(15),(16),(17),(18),(19),(20)}
2.4 非合作目标动态特性分析
在接近过程中,非合作目标往往具备翻滚、自旋、章动,甚至机动等运动,将这种运动定义为目标航天器的相对动态特性。为克服此类动态特性,追踪航天器在接近过程中,须进行闭环制导。本文对动态特性进行了分析,设计修正方法,作为后续制导律的设计实施的基础,以下分析均在Sto-0坐标系中进行,为便于阐述,变量定义如表2。
(a) 目标航天器机动
以针对非合作目标的后方接近任务为例,如图5所示,交会目标点为S=T+[0,-10,0]T,目标航天器进行机动,显著地改变了运行轨道,导致交会任务的终端位置持续发生改变,要求接近轨迹也做出改变。
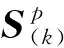
(22)
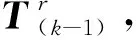

表2 变量定义表Table 2 Definition of variables
(23)
假设Er(k)=l(J,ρ,P,δ),表示由外界扰动和系统偏差造成的误差,式中,J,ρ,P,δ分别表示引力摄动、大气阻力、太阳光压和控制系统引起的偏差。并设计预测误差修正量
ΔRp(k-1)=Ep(k-1)+Er(k-1)
(24)


(25)
式中:Kv、Ka、Kr分别为相应的加权系数,可以根据系统性能灵活调整,一般取常数1即可。在得到S(k+1)点后,则可更新第k+1个制导周期的初始状态和终端状态,用于规划交会轨迹和控制指令。
(26)
上式为二步预测方式,最后的误差表达式为
(27)
由矢量关系可以将上式展开
KrΔRp(k-1)
(28)
式(28)可见,最终的制导主要误差由制导周期、目标航天器的加速度、系统误差和外界扰动决定,在工程实施中,选择合适的制导周期时长,同时满足星上计算速度和任务精度的要求是关键。
(b) 目标航天器自旋
假设是针对带有自旋状态的非合作航天器的绕飞或者定点观测等任务,由于绕飞任务大多都要求追踪航天器与目标航天器保持一定距离,还要增加禁飞区约束。在Sto坐标系下描述相对运动时,T(k)可以看成固定点,终端目标点S(k)随着目标航天器自旋发生改变。误差推导过程类似机动情况。最终的误差表达式为:
(29)
式中:
(30)
(31)
(c) 目标航天器章动
(32)
式中:
(33)
(34)
3 制导设计
目前对凸优化问题最有效的求解算法是原始对偶内点法(PDIPA),其本质是拉格朗日乘子法、牛顿法、障碍函数法的结合用,基本思路是在保持解的原始可行性和对偶可行性的同时,沿原对偶路径寻找最优解[13],在此过程中能始终维持原始解和对偶解的可行性。具有收敛迅速的优点,最显著的特点是迭代次数和计算量不会随问题规模增大而大量增加,限于篇幅,详细的解算过程,请参阅文献[12]。
根据凸优化算法计算快速的特点,本文针对自主交会任务,设计了基于凸优化的制导方案,该制导方法具备良好的鲁棒性,满足非合作目标的交会任务需求,具体步骤如下所述:
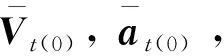
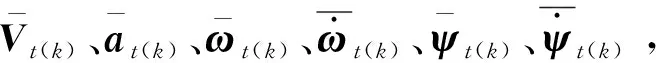
第三步:制导终止判断,在开始制导飞行后,立刻判断(k+1)·td是否等于tf,若是,则跳转第六步;若(k+1)·td 第四步:任务更新,根据第k-1制导周期内的相对导航系统测量结果,利用式(23)生成的制导误差Ep(k-1),Es(k-1)、Ez(k-1)类似;结合外界扰动与控制系统偏差,根据式(24)、(31)、(34)生成修正量ΔR(k-1)=ζ(Ep(k-1),Es(k-1),Ez(k-1),Er(k-1));根据式(25)预测目标在第k+1制导周期内目标航天器的相对状态T(k+1)、A(k+1);并根据式(26)生成S(k+1)、X0(k+1)和Xf(k+1);对任务状态进行更新,更新交会任务总时长,令tf(k+1)=tf-k·td,再定义k=k+1;调整约束与目标条件,更新RPOs任务模型,跳转第五步。 第五步:任务解算,运用原始对偶内点法求解凸化RPOs问题,生成第k+1制导周期规划轨迹和姿态,及控制命令U(k+1)、M(k+1),当t=k·td,即完成第k个制导周期的控制飞行后,跳转第二步。 第六步:结束制导,追踪航天器根据最后一次规划结果执行制导飞行。 假设追踪航天器进行-V-bar接近任务,目标航天器进行变加速度的规避机动。给定方锥形轨迹约束,将外界扰动用随机函数代替。仿真参数如下: 假设目标航天器机动参数: 令kf=tf/td,则最后一个制导周期终端状态变为: 仿真结果如图9-10所示。主要的轨迹变化集中在轨道平面内,因此仅给出该平面的制导轨迹。 假设目标航天器存在自旋运动,追踪航天器需进行定点观测任务,存在相对距离为10m的圆形禁飞区约束,其他任务条件不变,初始相对轨道状态与终端相对轨道状态变为: 假设目标航天器自旋状态参数: 经制导仿真计算,交会接近轨迹如图11所示,其它仿真曲线与算例 1类似,略。 假设目标航天器存在章动,追踪航天器需进行-V-Bar接近任务,各仿真条件与算例1类似。 假设目标航天器章动状态参数: 经制导仿真计算,交会接近轨迹如图12所示,其它仿真曲线与算例 1类似,略。 图9、图11、图12表明,针对具备动态特性的非合作目标的自主交会接近问题,本文提出基于凸优化的制导算法,求解的接近轨迹过渡平滑,符合各类轨迹约束,同时,也能很好地克服动态特性带来的不利影响。图10表明,为了克服非合作目标航天器动态特性的影响,消除各类误差,每一个制导周期内必须施加修正推力,推力大小、力矩大小均满足约束要求,相对位置、相对姿态曲线过渡平滑,良好地实现了交会接近任务。 本文针对非合作目标的自主交会接近任务,重点分析了非合作目标的机动、自旋和章动等动态特性对追踪航天器的制导误差;结合某航天器的姿轨控一体化推进系统配置,提出一种基于凸优化算法的制导方案;并对非合作目标机动、自旋和章动情况下的自主交会任务进行了数值仿真,结果表明:该方法成功解决了非合作目标交会接近任务中的制导问题,并具有良好的鲁棒性,有效地抑制了各类动态干扰和误差,为面向非合作目标的交会接近任务提供了一种合理可行的制导方法。4 仿真校验
4.1 算例1:目标航天器机动
4.2 算例2:目标航天器自旋
4.3 算例3:目标航天器章动
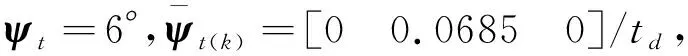
4.4 仿真结果分析
5 结 论

