借助图形发展学生的推理能力

浙江温州市百里路小学 郑美娜

推理能力是《义务教育数学课程标准（2011年版）》（以下简称《标准》）中提出的小学数学十大概念之一，东北师大马云鹏教授在《关于数学核心素养的几个问题》一文中更是强调：《标准》中的十大概念其实就是义务教育阶段的十大数学核心素养。由此可见，作为小学数学十大核心素养之一的推理能力，是学生数学素养的重要内容。

那么，在日常小学数学教学过程中，我们怎样发展学生的推理能力呢？方法和途径很多，以图形为载体培养小学生的推理能力就是一种非常有效的方法。

一、通过“数图结合”发展学生的推理能力

提到推理能力，很多教师认为这不是每个学生都具有的能力，因为它需要通过思维训练来完成，让学有余力的同学去奋斗吧！事实上，课堂教学中时时都有发展机会，就连我们日常最普通的计算教学，也能通过数图结合的方法来发展学生的推理能力。如学生在学习了五年级下册“分数加减法”后，数学练习题中有这样一道题：你能很快地算出下面算式的结果吗？，如果只是想让学生知道和掌握这道题的计算方法与计算结果，那显然是不够的，我在指导此内容时直接出示：

师：不让你通分，不让你把分数化成小数，你能快速、准确地计算出这道题的结果吗？（生疑惑，表现出无能为力的样子）

师：看来需要老师的帮助了是吗？说吧，需要老师提供什么帮助？

生开玩笑地说：老师，你帮我们算出来吧！

师：想得美！再说这也太不能体现你们的水平了，再想想！（生实在没办法）

师：如果老师给你这组题目和图形，仔细观察，你发现了什么？

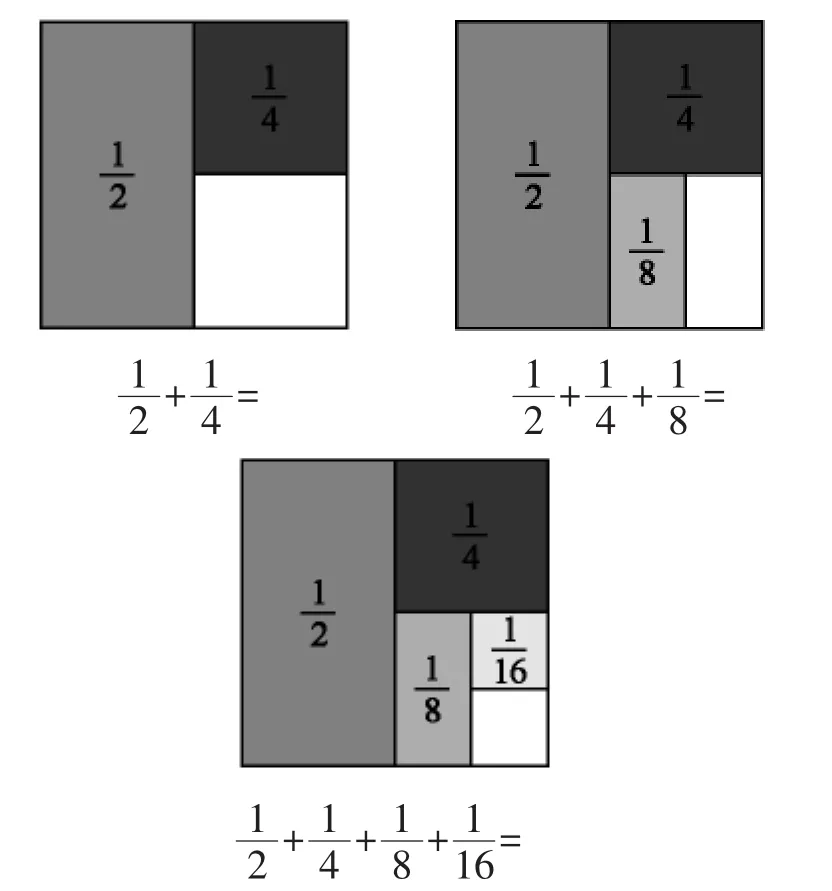
学生通过仔细观察题目和图形后，先是恍然大悟，然后是大彻大悟的样子：“原来如此！”于是很快得出：

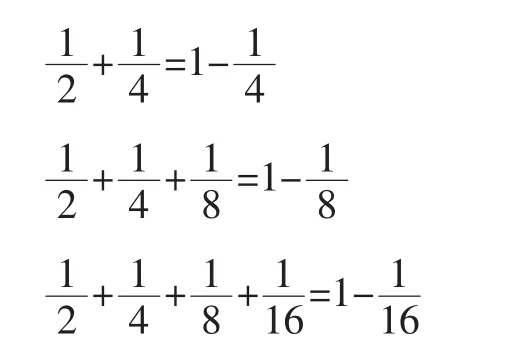
生：能！（自信满满并很快算出正确结果）

师：能自己出一道这种题目考考同桌吗？

生：能！（学生出题）

师：怎么知道自己做得是否正确？（学生通分验证知道有误）怎么办？能否也照样借助图形来解决？（生齐说能），随后出示下图：

师：现在有什么发现？

师：有什么想说的吗？

生：图形的作用真大！

师：体现在哪？

……

这组题目并没有到此为止，趁学生由前面产生的兴趣我继续借助图形来研究如：……和等题目。

由此可见，数图结合有利于问题解决，更有利于推理能力的发展。上述案例原为一道道普通的分数计算题，现以图形为载体进行数学推理，化难为易、化抽象为直观，轻而易举地使问题得到了解决，在很大程度上提升了计算教学的价值。更有意义的是，对学生的数学思维发展以及概括思想、极限思想和模型化思想等进行了有效指导和训练，进一步促进了学生推理能力的发展。

二、利用图形操作发展学生的推理能力

实践操作是小学生获得数学知识和深入理解数学内涵的重要途径，一些数学规律的发现和方法的探究，都是通过观察、操作、比较、分析、推理得到的，现以我校一位教师的《圆的认识》教学片段来例证：

（学生认识了圆的各部分名称）

出示问题：以C点为圆心，画出A、B两点都在同一个圆上的圆形（如下图）。

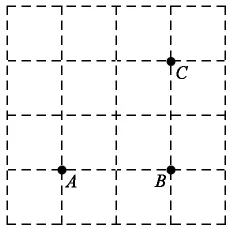
师：题目有什么要求？

生：A、B两点都在同一个圆上。

师：那就画吧。（一部分同学马上拿起圆规就画，一部分同学在沉思，没动手画）

师：画好了吗？刚才老师看到一部分同学非常认真地画图，另有部分同学却没画，我先问画的同学，你们画出来了吗？（没有）为什么？

生：好像画不起来，A、B两点总不能都在圆上。

师：我要问问没动手画的同学，你们为什么不画？

生：这个要求不行，不可能画出来。

师：为什么？

生：如果要让A、B两点都在同一个圆上，那么圆心C点到A、B两点的距离要相等，而这里的AC不等于BC。

师：现在你们知道为什么不能画出以C点为圆心，A、B两点都在同一个圆上了吗？（知道）那好好思考一下，请问C点在哪里就能画出A、B两点都在同一个圆上？

学生经过操作、讨论、思考和分析后。依次展示出下列作品：

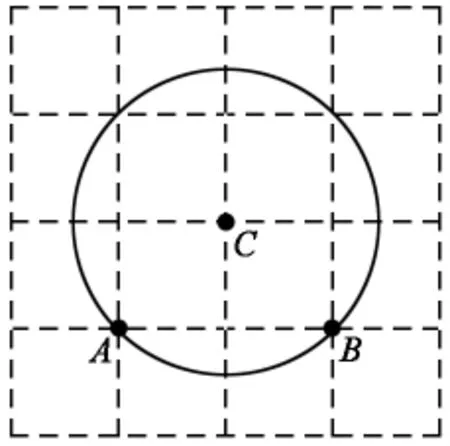
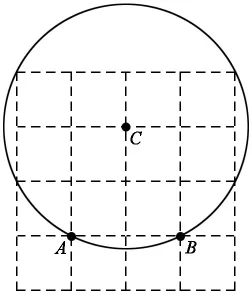
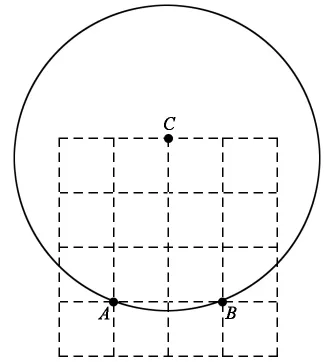
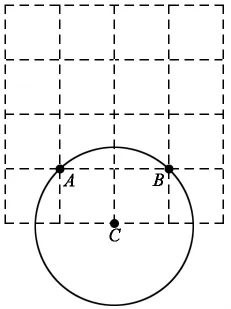
师：通过刚才的画图操作，有什么想说的？

……

师：如果想让A、B、C三点都在同一个圆上，圆心又该定在哪里？

……

为落实本课的一个重要教学目标——圆的特征，教师没有直接告诉学生要研究圆的特征，而是给学生足够的时间和空间，引导学生通过动手画图操作、观察、思考、推理和发现，引发学生认知冲突。学生通过画一画、看一看、比一比、想一想等活动来解决问题，得出结果。如圆有大小之分、同圆或等圆的所有半径相等、半径决定圆的大小、圆心决定圆的位置等知识的获取，不是依赖教师的教，而是学生在动手操作的过程中加入思考与推理等思维活动，提升了实践操作的价值和意义，丰富了课堂教学，真正感受到了抽象和推理的力量。

三、在图形静动态变换中发展学生的推理能力

“图形与几何”领域是发展学生推理能力的沃土，如图形认识、图形位置、图形运动等问题的解决都需要用到推理。教材中以图形为载体发展学生推理能力的素材很多，效果也很好，现以另一位教师的教学片段来例证：

（出示下图）

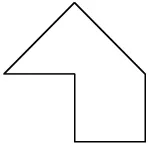
师：仔细观察，你觉得这个图形有趣吗？

生：有趣。

师：为什么你觉得这个图形有趣？

生1：因为它像小马的头，很可爱。

生2：它像不完整的房子，很有趣。

生3：它像倒挂着的靴子。

……（氛围轻松，学生畅所欲言）

师：你们说得都很形象，说明你们很热爱生活。作为数学老师的我，心里想的和你们想的可不一样哦，谁能猜猜，老师看到的是什么？心里想到的又会是什么？

（经老师一提醒，学生自然往数学图形知识方面去思考）

生1：左边是一个三角形，右边是一个梯形。

生2：上面是一个三角形，下面是一个正方形。

师：你们的眼睛真亮！不过，老师还有一个重要的事情要让你们去做，再仔细看看这个图形，你能否用剪刀把它直直地剪一刀，再拼成另一个图形。记住，是直直地剪一刀！先独立思考，有想法后再跟同桌交流。

生1：把左边的三角形剪下，拼到右上角后变成了一个长方形。

生2：还可以把右下角的三角形剪下，把左下角补上就变成了一个正方形。（很多同学恍然大悟）

在“图形与几何”教学中，往往存在两个不足：一是更多关注单个图形的概念和表象，忽视基本图形之间的相互联系和区别；二是更多关注图形静止状态下的特点和知识，忽视变化图形之间的关系。上述这个教学案例很好地弥补了这两个不足，执教者不仅引导学生对图形有静态意义上的认识和理解，更重要的是有目的地让学生把静态的图形引向有效的动态想象，赋予图形生命，对观察和想象到的图形在脑子里进行一次次的信息筛选、梳理、提取和图形重建，加深了对图形的认识和理解，不仅有利于学生空间观念的认识，更有利于学生推理能力的发展和数学素养的提升。

“推理能力的发展应贯穿在整个数学学习过程中”。由此可见，推理能力的培养需要经过一个长期和缓慢的过程。因此，我们只有牢牢立足于课堂教学这块沃土，紧紧把握新《标准》要求，用心思考，从实际出发，多研究教材、多研究课堂和学生，才能使学生的推理能力得到良好的发展。♪