立足课堂，提升学生数学素养

江苏南京致远外国语小学分校 王 静

数学素养指主体在已有的数学经验的基础上，在数学活动中通过对数学的体验、感悟、反思，并在真实情境中表现出来的一种综合性特征。笔者认为，用简单的一句话概括就是“具备一定的数学思维”。《义务教育数学课程标准（2011年版）》指出：数学素养是现代社会每一个公民应该具备的基本素养。那么，如何在课堂教学中提升学生的数学素养？

一、创设情境活动——提升学生数学素养的立足点

学生学习的过程是一种认知的过程，将学生置身于情境中，不仅丰富了教师的教学方式和学生的学习方式，而且激发了学生学习的主动性和积极性，帮助学生理解，发展数学思维。例如，在教学苏教版二年级下册《认识厘米》一课时，教师可以设计以下情境：

天气渐渐冷了，动物们都开始准备过冬的食物了。熊大和熊二收集了一大罐的蜂蜜，熊大负责将蜂蜜藏了起来。

熊二悄悄地问：“熊大，你将蜂蜜藏哪了？”

“我从屋后的大树下往东量了6脚，挖个洞埋了进去。”

可是，哥俩的秘密被光头强听到了。他想：大树往东走6脚，我去把它挖走。他立刻找来铁锹，从大树下往东走了6脚，到了，就在这了！挖呀，挖呀，可是什么也没有挖着。这是怎么回事呢？

师：同学们，这是怎么回事呢？

生：因为光头强的脚跟熊大的脚不一样大。

师：有道理！ 咱们请熊大走走看，1、2、3、4、5、6，哇，蜂蜜在这呢！

追问：都是走6脚，比一比，你发现了什么？

生：我发现熊大的脚大，走得远，光头强的脚小。

师：同学们观察得真仔细！熊大的脚长，光头强的脚短，因此他们度量的标准是不同的，所以同样走6个脚长，获得的结果也是不一样的。如果想获得一样的结果，该怎么办呀？

生：要用一样的标准。

师：是呀，我们在测量长度的时候，要有统一的标准，这就是长度单位（板书）。今天我们就来认识长度单位中的一个：厘米。（板书课题）

通过以上案例我们发现，学生能够将自己投入到情境活动中，感受到熊大和光头强的“6脚”不一样，从而产生统一标准的需求。这个情境贯穿了本节课，在量几厘米时，熊大过生日收到光头强送来的礼物——尺子，可是，熊大和熊二拿着尺子比画了半天，也不知道怎么量，教师自然地把问题抛给学生。情境活动让学生融入学习，在学习需求的内驱力作用下，充分发挥学生主体性作用，养成思考的习惯。这样，为学生学好数学创造了良好的条件。

二、设计操作活动——提升学生数学素养的生长点

教育家苏霍姆林斯基曾说：“儿童的智慧在他的手指尖上。”学生的思维离不开动作，动手操作是智慧的源泉，是发展的起点。动手操作建立了表象思维，培养了学生数学观察、分析、总结的能力，提升了学生的数学素养。例如，在教学苏教版三年级上册《间隔排列》时，教师可以设计操作活动，培养学生的数学素养，详细情况如下：

师：4个□和（ ）个△一一间隔排列？

活动要求：

（1）想一想，想要和4个□一一间隔排列，需要几个△？

（2）拿出□和△，把你们刚才想的摆一摆，摆好一种就在练习纸上画一画，然后继续摆，继续画，能摆几种摆几种。

（每个学生动手操作，教师巡视）

汇报展示：

师:同学们真厉害，通过自己动手操作，找到了这么多摆法。这四种都是一一间隔排列，数一数，每排正方形和三角形的个数分别是多少呢？

学生汇报，教师板书。

师：想要和4个正方形一一间隔排列，需要几个三角形？

生：三角形的个数可以是3个，还可以是4个，还可以是5个。

师小结：看来，动手操作确实能够帮助我们解决问题。

操作活动是学生数学学习的重要方式，数学知识和结论不是由教师告诉学生的，而是让学生在教师的指导下自主发现，并获得结论。所以，操作活动在培养学生能力、发挥学生个性特长等方面起着重要作用。在本节课中，教师通过实际操作激发了学生的探究欲望，让学生充分体验了寻找规律完整的过程。教师让学生摆三角形和已知的4个正方形构成一一间隔排列，有的学生摆出了首尾不同的两种情况，有的学生摆出来首尾相同的两种情况。这里充分利用学生自己创作的资源进行观察和思考，调动了学生学习的积极性，也是学生探究间隔排列规律的重要感知，这是学生初步了解规律后的第一次尝试。每个学生通过动手操作感悟知识形成的过程，提升了学生数学素养的生长点。

三、创编习题——提升学生数学素养的助推点

我国著名数学家华罗庚曾说：“学数学而不做数学题，等于入宝山而空返。”由此可见习题练习是学生学习过程中不可或缺的部分，而发掘每道习题所蕴含的数学素养更是重中之重。那么，教师需要在分析教材习题的基础上，根据学生学习特点自主创编习题。

（一）分析教材习题，转换看题角度

教材中每一道练习题并不仅仅是让学生做对那么简单，教师在习题处理上应该多往数学素养方面想一想，让学生产生对教材习题深入发掘的需要。一年级下册中有这样一道题，最初笔者是这样分析的：

经过一段时间的学习，笔者将上述数学素养的分析修改为：观察表格，让学生利用两位数加、减两位数的竖式计算解决“小明一共跳多少下”和“小娟第二次跳多少下”的问题，培养学生观察表格的能力，能够用完整的三句话说出表格中蕴含的数学信息。再通过“你还能提出什么问题”引导学生利用给出的条件提出问题、解决问题，培养学生善于动脑，积极发现和解决问题的品质。

笔者认为多花一些时间在教材习题的分析上，尽量做到多角度去思考、处理习题，不但不会浪费时间，反而对自己和学生成长有着不容忽视的作用。

（二）创编拓展习题，提升数学素养

维果斯基的“最近发展区理论”认为，学生的发展有两种水平：一种是学生的现有水平，指独立活动时所能达到的解决问题的水平；另一种是学生可能的发展水平，也就是通过教学所获得的潜力。两者之间的差异就是最近发展区。教学应着眼于学生的最近发展区，为学生提供有难度的内容，调动学生的积极性，发挥其潜能，超越其最近发展区而达到下一发展阶段的水平，然后在此基础上进行下一个发展区的发展。在课堂教学中，教师应立足学生的发展，以提高学生的学习质量、发展数学思维为目的，创编拓展习题。

在教学苏教版五年级上册三角形面积计算时，根据面积计算公式：三角形的面积=底×高÷2，学生知道等底等高的三角形面积相等。为了加强学生对等底等高三角形面积的深刻的理解，笔者创编了一组习题。

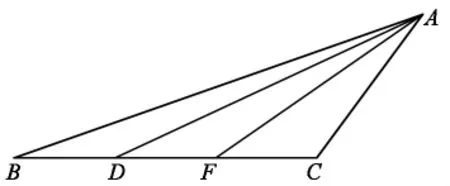
习题一：D、F是BC边上的三等分点，你能找到面积相等的三角形吗？

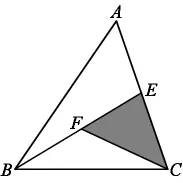
习题二：下图中△ABC的面积是16平方厘米，E、F为所在边的中点，求阴影部分的面积。

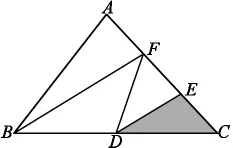
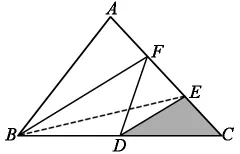
习题三：如图，在三角形ABC中，D是BC边上的中点，E、F是AC边上的三等分点，阴影部分的面积是12平方厘米，求三角形ABC的面积。

解读习题

习题一中D、F是BC边上的三等分点，所以BD=DF=FC,△ABD、△ADF、△AFC等底等高， 面积相等，此题较为容易；习题二在上一题的基础上，寻找面积相等的三角形，不难发现，BF=FE,△EFC和△BFC等底等高，面积相等。同理，△BEC和△ABE面积相等，也就是说，阴影部分的面积是△ABC面积一半的一半，算式是16÷2÷2=4（平方厘米）；习题三的图形更为复杂，学生寻找到一些等底等高的三角形，如△EDC和△FDE,△FDC和△FBD，这时可以求出S△FBC=12×2×2=48 （平方厘米），此时缺少△ABF的面积，大部分学生找不到与它等底等高的三角形。教师引导学生思考△ABF和△FBC底和高的关系，高相等，底是它的一半，面积就是它的一半，所以S△ABC=48÷2+48=72（平方厘米）。 教师引导学生如果给图形添上辅助线呢？如下图，通过添加辅助线，转化成与习题二一样的题型。

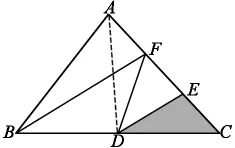
教师在原有的基础上创编习题，层层推进，引导学生利用已有知识灵活解决问题，让学生练得透彻，练出能力，培养思维，提升数学素养。

数学素养的提升不是一朝一夕的事，要通过长期的培养、积淀。教师要关注课堂，创设情境活动，设计操作活动，创编习题，找到每节课的素养点，创造有效的数学活动，开拓数学思维，提高解决问题的能力，发展数学素养。♪