一类满足线性递推关系的行列式的特征根解法
黄家云
1 背景介绍
行列式的计算是线性代数中一个重要而基础性的问题。因为行列式的类型千变万化,所以行列式的计算方法也五花八门。其中,满足递推关系的行列式因为其连续两阶或三阶之间具有特殊的规律性,一直吸引着研究者的兴趣,由此发展出了关于满足递推关系的行列式的一些算法,如:数学归纳法、递推法等[1]。
在二阶常微分方程中,常系数线性齐次微分方程因为未知函数的原函数、一阶导数、二阶导数三者满足线性关系,由此通过建立特征方程,进一步根据特征根的情况讨论其通解[2]。受此启发,如果一个行列式连续三阶之间也满足线性关系p·Dn+2+q·Dn+1+r·Dn=0,这里p,q,r均为实数,那么能不能通过建立特征方程,并根据特征根的情况来推导其通项公式呢?通过推导,可以得到关于满足线性递推关系的行列式的通项公式。
2 主要结论
定义 设行列式D满足线性递推关系p·Dn+2+q·Dn+1+r·Dn=0,称方程p·λ2+q·λ+r=0为D的特征方程,称方程p·λ2+q·λ+r=0根为D的特征根。
定理 设行列式D满足线性递推关系p·Dn+2+q·Dn+1+r·Dn=0,则有:
(1)如果D的特征根为λ1≠λ2,那么Dn=a·λ1n-1+b·λ2n-1;
(2)如果D的特征根为λ1=λ2=λ,那么Dn=(a+n·b)·λn-1。
注: 上述通项公式Dn中的a,b是待定常数,可通过n=1,2求得。
证明数学归纳法
(1)假设当行列式的阶数小于等于n+1时,结论成立,即有:
Dn=a·λ1n-1+b·λ2n-1
那么由递推公式p·Dn+2+q·Dn+1+r·Dn=0,可得
(*)
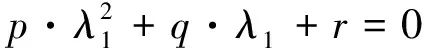
不难验证,当Dn+2=a·λ1n+1+b·λ2n+1时,(*)式成立,即:

3 应用举例
利用上面定理的结论,可以推导出连续三阶满足齐次线性递推关系的行列式的通项公式。
例1计算n阶行列式
解按照第一行展开得
Dn=-Dn-2即Dn+Dn-2=0
于是特征方程为x2+1=0,解得特征根为x1=i,x2=-i。
从而,可令Dn=a·in-1+b·in-1,当n=1,2时有:
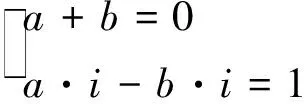
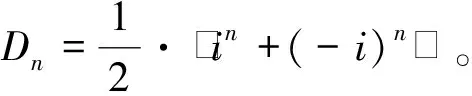
例2计算n阶行列式
解按照第一行展开得Dn=9Dn-1-20Dn-2即Dn-9Dn-1+20Dn-2=0。
于是,特征方程为x2-9x+20=0,解得特征根x1=4,x2=5。
从而Dn=a·4n-1+b·5n-1,当n=1,2时有:

所以,Dn=5n+1-4n+1。
例3计算n阶行列式
Dn=

解(1) 当α=0时,Dn=βn。
(2)当α≠0时,将行列式按照第一行展开得:
Dn=(α+β)·Dn-1-α·β·Dn-2
也即
Dn-(α+β)·Dn-1+α·β·Dn-2=0。
特征方程为
x2-(α+β)·x+α·β=0,
解得特征根为:
x1=α,x2=β。
针对α与β的关系,讨论如下:
(I)当α=β≠0时,令Dn=(a+b·n)·αn-1。当n=1,2时有:
解得
a=b=α,
从而
Dn=(n+1)·an。
(II)当α≠β时,令Dn=a·αn-1+b·βn-1。当n=1,2时有:
解得
所以
微分方程与线性代数本是属于数学的两个不同领域,其研究对象和背景可谓风马牛不相及。但是,他们在解决问题的思想上却可以一脉相承如出一辙。由此可见,数学思想的迁移是数学解决问题灵活性的展现。数学思想的迁移,源于不同数学对象之间的相似类比,在形式上相似的事物或问题在研究思路或解决的思想上往往是相通的。

