有序分位加权集结算子及理想激励点的模拟求解

李伟伟,易平涛,郭亚军

(东北大学工商管理学院,辽宁沈阳110169)

1 引 言

信息集结是将多种来源的信息融合为一个整体的过程,是多属性决策领域一项重要的研究内容.迄今为止,关于信息集结方法的研究在众多学者的共同努力下已取得了丰硕的理论成果[1-8].进一步,为提升理论方法解决实际问题的能力,在理论研究中考虑决策者的需求也十分必要.众所周知,激励是一种重要且常见的管理手段,在信息集结过程中准确而自然地融入决策者的激励偏好,能够对被评价对象的发展(尤其长期发展)起到持续有效地引导作用.

目前,已有部分学者对体现激励特征的信息集结方法展开研究.易平涛等[9]用直线型的激励控制线表达决策者的激励偏好,对被评价对象的发展趋势进行激励,提出了一种基于双激励控制线的动态信息集结方法,并进一步将其拓展至泛激励控制线的情形[10].刘微微等[11,12]在体现被评价对象发展趋势的基础上,融入对被评价对象变化速度的考虑,在双激励控制线的基础上提出了兼顾发展速度的动态信息集结方法.文献[13]在双激励的基础上,提出了按层级激励的信息集结方法.马赞福等[14]考虑被评价对象在不同时刻发展水平的差异,提出了一种基于属性值增益水平的信息集结方法.张发明[15]在文献[14]的基础上做了进一步的拓展,以显性激励为基础,加入隐性激励,提出了双重激励的信息集结模型.

总结上述信息集结方法,发现一个共同的特点,即上述方法多是对被评价对象发展趋势或状态的“整体激励”,这种激励模式能够对被评价对象的发展起到一定的引导作用,但决策者的激励偏好却通常被隐藏于激励模型的计算中,且模型的数值过程一般都比较复杂,因而会导致被评价对象对决策者激励偏好的感知与反馈比较笼统,落实到被评价对象的行为引导上,就会出现被评价对象大多选择模糊地提升自身在各方面(属性)的取值,却不明白如何采取最优的行动方案以获取最大程度的激励成果.

针对上述问题,本文给出了采用“分段激励”的方式对被评价对象进行诱导性激励的解决思路.论文的主要创新之处是以分布分位数的方式衡量被评价对象的相对发展水平,并以分布分位数为基础,对决策者的激励偏好进行细化描述,提出了有序分位加权集结算子的方法.进一步采用随机模拟的思路分析了理想激励点的求解方法,以算例的形式验证了该方法的有效性,并得出当采用正向双点激励方式时,不仅能够实现对被评价对象的奖惩并重,且能够通过奖惩凸显被评价对象之间差异的结论.与已有文献中“整体激励”的方式相比,本文给出的“分段激励”和有序分位加权集结方法,能够更加细腻地刻画决策者的激励偏好,同时能使被评价对象对决策者的激励偏好有着更清晰的认识,从而实现对被评价对象系统性发展的良性引导.

2 有序分位加权集结算子

该部分首先对衡量被评价对象在各属性上相对发展程度的分布分位数进行求解,然后基于分布分位数构建有序分位加权集结算子,在此基础上研究体现激励特征的属性权重(称之为“分位权重”)的计算方法.

2.1 分布分位数的求解

对由n个被评价对象(o1,o2,...,on)及m个属性(x1,x2,...,xm)构成的n×m维决策矩阵为[xij]n×m,不失一般性,令m,n≥3.通常,实际问题中被评价对象关于某属性xj,j=1,2,...,m的取值存在一个理想的上限和可接受的下限,分别记为Mj和mj.参照无量纲化方法中的“极值处理法”[16],下面对分布分位数的定义进行界定.

定义1对被评价对象oi在属性xj上的取值xij,称

为与属性值xij对应的分布分位数,有qij∈[0%,100%].

由定义1可知,qij的取值越大,代表被评价对象oi在属性xj上的相对发展程度越高.除用于衡量被评价对象的相对发展程度之外,分布分位数的另一个作用是为决策者激励偏好的表达提供了便利.下面以图1为例,对其进行简单说明.图1中,黑色圆点表示某被评价对象属性值的分布分位数,α1和α2为决策者给出的两个激励点,其取值介于0%～100%之间.因而可将图1视为由两个激励点区分的3段激励子区间,即[0%,α1),[α1,α2),[α2,100%].不失一般性,决策者的激励偏好可表述为,对分布分位数分布于[0%,α1)子区间内的属性值给予惩罚;对分布于[α1,α2)内的属性值不惩罚也不奖励;对分布于[α2,100%]内的属性值给予奖励.

图1 基于分布分位数的激励偏好示意图Fig.1 Diagram of incentive preference based on quantile

2.2 有序分位加权集结算子的构建

定义2对被评价对象oi在m个属性上的取值(xi1,xi2,...,xim),按其对应的分布分位数由小到大的顺序进行排序,得到有序数对则有称

为被评价对象oi的有序分位加权集结值,其中为与有序数对〉对应的分位权重,满足且

2.3 分位权重的计算

定义3对属性值xij,设其对应的分布分位数分布于激励子区间[αt,αt+1),t=0,1,...,k,则属性值xij的分位权重系数为

式(3)的构建保证了发展程度分布于同一激励子区间内的属性值所获奖惩幅度相同,但可依据(qij-αt)/(αt+1-αt)进一步调整不同属性值对应的分位权重系数的大小.此外,由式(3)可以看出,分布于不同激励子区间内的属性值的分位权重的取值区间也不尽相同.因而,通过式(3)可在实际应用中实现对不同发展程度的属性值的差异奖惩.

由定义3可知,分位权重的求解与激励系数相关,而对激励系数的求解可借鉴Yager[2]提出的orness系数的测度方法,这里将其定义为激励偏好系数(记为Ip),则有

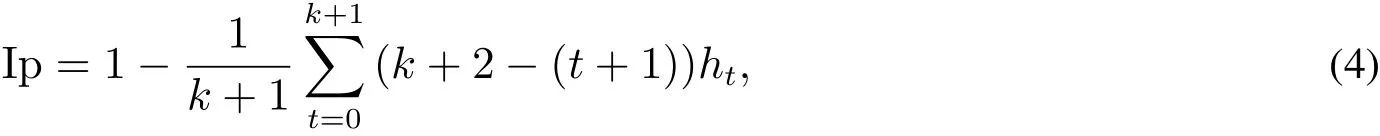
其中Ip∈[0,1].

为保证激励偏好的一致性,激励系数h0,h1,...,hk+1之间的大小应依次递增或递减,即当激励系数之间大小关系依次递增时,有ht+1＞ht,t=0,1,...,k,表明决策者偏好于相对发展程度较高的属性值,此时有Ip∈(0.5,1],这里称此种情形为“正激励”;相反地,当ht+1＜ht时,Ip∈[0,0.5),表示决策者偏好于相对发展程度较低的属性值,此种情形被称为“负激励”;除此之外,当ht+1=ht=1/(k+2)时,Ip=0.5,表示无论属性值的相对发展程度如何,决策者给出的激励偏好相同,此种情形被称为“无方向均等激励”.由上述分析可以看出,式(4)的构建思路是通过激励系数大小关系的设置将决策者不同程度及不同方向的激励偏好融入同一表达式中,从而使得实际应用中决策者激励偏好的表达更具灵活性.

基于上述分析,依据适度激励原则,可通过以下规划模型求解激励系数,然后将求解得到的激励系数代入式(3)即可得到对应的分位权重.

规划模型为

上述规划模型的合理性体现于,目标函数的设置使得激励系数的均方差最小,目的是为了缩小不同激励子区间激励系数之间的差异,从而实现适度激励的效果;约束条件通过激励偏好系数和激励系数大小关系的设定,兼顾了正激励和负激励两种情形,从而提升了运用该模型解决实际问题的应用空间.

3 激励点的确定原则

对有序分位加权集结算子用于解决激励问题的基本过程进行总结,具体如下.

步骤1对某决策矩阵,依据式(1)求解被评价对象在各属性上的分布分位数;

步骤2决策者提供激励点,据此分析各被评价对象在不同激励子区间内的分布情况;

步骤3基于决策者的激励偏好(系数),依据式(4)～式(6)求解激励系数,将求解得到的激励系数代入式(3)求得各被评价对象的分位权重;

步骤4将(规范化处理后的)属性值、对应的分布分位数及分位权重代入式(2),计算得到带有激励特征的集结值,并依据集结值大小对被评价对象进行择优或排序.

实际应用中,激励措施的采用,除能够通过分段激励的方式让被评价对象清晰明白自身的发展水平从而对其起到直接引导作用外,激励措施的另一个作用就是为了凸显被评价对象之间的差异,从而使得被评价对象看清自身与其他被评价对象之间的差距,以对其发展起到间接的引导作用.由上述有序分位加权集结算子的应用步骤可知,在这一过程中起关键作用的是决策者给出的激励点的位置.理想的激励点应分布于所有被评价对象分布分位数的取值区间内,从而实现对被评价对象发展的“直接引导”(或“内部激励”),同时也应能够最大程度地区分不同被评价对象集结值之间的差异,实现对被评价对象的“间接引导”(或“外部激励”).基于此,下面给出确定理想激励点的两条基本原则.

原则1内部激励.决策者给出的激励点应分布于所有被评价对象分布分位数的取值范围内.

原则2外部激励.决策者给出的激励点应使所有被评价对象最终集结值之间的差异最大.

对原则1,设被评价对象oi关于m个属性的分布分位数集合为{qi1,qi2,...,qim},则理想激励点αl,l=1,2,...,k的取值范围为αl∈[min(qij),max(qij)],i=1,2,...,n;j=1,2,...,m.

对原则2,设集结值之间的差异用两个集结值之间的偏差衡量,因而理想激励点的给出应使集结值之间的最小偏差最大化,即激励点αl的给出应使min(|yi-yk|),i≠k最大.

4 理想激励点的模拟求解

基于寻找理想激励点的两条原则,下面给出求解理想激励点的基本过程.

步骤1对某决策矩阵,求解对应的分布分位数矩阵;

步骤2决策者给出激励偏好系数Ip及激励点的个数;

步骤3在分布分位数的最大值与最小值之间随机取定激励点,依据激励偏好系数Ip、式(3)～式(6)求解分位权重,将属性值和分位权重代入式(2)计算得到被评价对象的集结值;

步骤4计算所有被评价对象集结值之间的最小偏差,重复步骤3,寻找能使该最小偏差最大的激励点.

由上述理想激励点的求解过程可知,理想激励点的寻找是在分布分位数的最大值与最小值之间“随机寻优”的过程,因而随机模拟仿真的方法可作为独立组件融入到该寻优过程中,不仅可提升该过程的可操作性,同时可节约求解的时间成本.下面对理想激励点的随机模拟求解步骤进行归纳.

步骤1对决策矩阵[xij]n×m,计算其分布分位数,并将分布分位数矩阵中的最大值和最小值分别记为qmax和qmin;

步骤2设置仿真次数监控变量count(初始值为0),设置存储变量σ0(初始值为0),αl,α2,...,αk(设决策者给定k个激励点,初始值为0);

步骤3count←count+1,在区间[qmin,qmax]内按均匀分布的方式随机生成k个随机数(激励点),记为r1,r2,...,rk;

步骤4基于决策者给出的激励偏好系数Ip计算各被评价对象的分位权重,并按有序分位加权集结算子的方式对(规范化处理后)决策信息进行集结,得到被评价对象的集结值yi,并计算集结值之间两两偏差的最小值,记为σ;

步骤5若σ＞σ0,则σ0←σ;α1←r1,α2←r2,...,αk←rk;

步骤6若count=sum(sum为决策者给出的仿真总次数,一般[qmin,qmax]区间范围越大,sum值越大),转入步骤7,否则转入步骤3;

步骤7保存σ0和α1,α2,...,αk的数值,退出程序.

通过上述模拟仿真得到的激励点α1,α2,...,αk即为理想激励点.

5 应用算例

对某公司5名员工在出勤情况(x1),销售业绩(x2),工作积极性(x3),学习能力(x4),客户满意程度(x5)和工作创新性(x6)的表现进行绩效评价.5名员工的绩效数据见表1.

由问题描述可知,6个考核项均为效益型属性,依据式(1)求得员工在各考核属性上的相对发展程度(分布分位数)如表2所示,其中各考核属性得分的理想上限为10分,可接受的下限为1分.

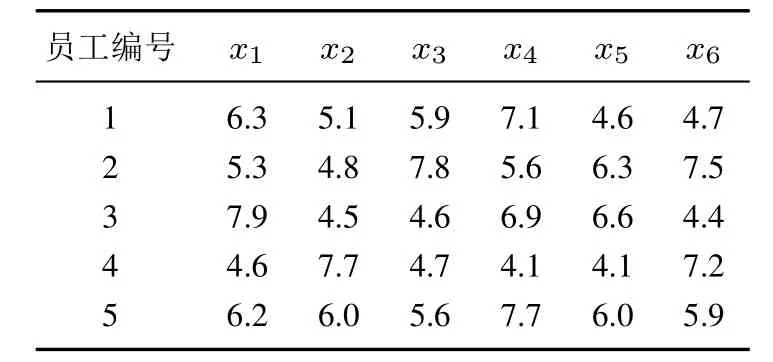
表1 员工在各考核属性上的绩效得分Table 1 Performance score of employees in each assessment attribute

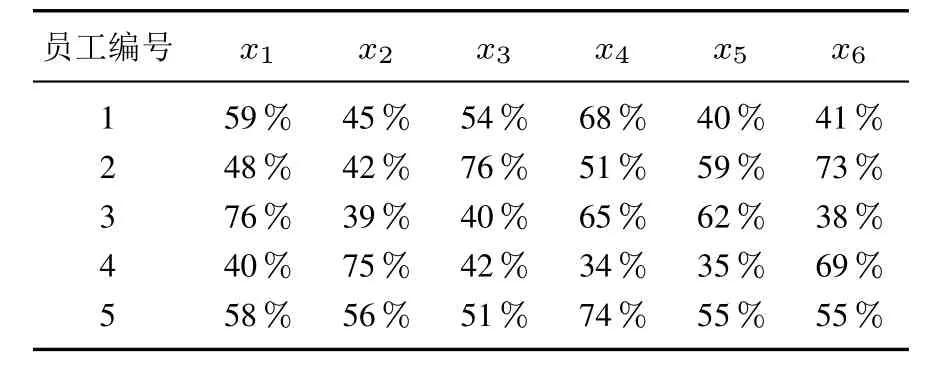
表2 员工在各考核属性上的分布分位数Table 2 Distribution quantiles of employees in each assessment attribute

1)激励点求解

依据理想激励点的模拟仿真步骤,激励点的随机取值区间为[34%,76%].下面分别就决策者给出1个和2个激励点的情形进行模拟仿真(单激励点仿真10万次,双激励点仿真100万次),仿真结果分别如表3和表4所示.需要说明的是,由于员工在各考核属性上的得分区间相同(为[1,10]),所以无需对得分值进行标准化处理.

表3 单激励点情形下的模拟结果Table 3 Simulation result under single incentive point

表4 双激励点情形下的模拟结果Table 4 Simulation result under double incentive points

2)结果分析

(a)不同激励偏好系数下的激励点的变化分析

为便于观察,绘制不同激励偏好系数下激励点的变化趋势图,见图2.需要说明的是,为作图方便,图2中Ip=0.5时的激励点取其他激励偏好系数下激励点的均值.

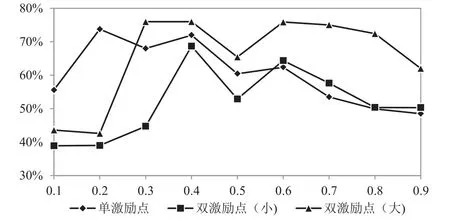
图2 不同激励偏好系数下激励点的变化趋势Fig.2 Variation tendency of incentive points under various incentive preference coefficients

观察两种激励情形下激励点的变化情况,可以发现无论是单点激励还是双点激励,“负激励”(Ip＜0.5)时,不同激励偏好系数下激励点的变化幅度均大于“正激励”时激励点的变化幅度,表明负激励时激励点对决策者激励偏好系数的敏感程度大于正激励时的敏感程度.

(b)不同激励偏好系数下各员工集结值的变化分析

当激励偏好系数在0.1～0.9之间变动时,分别绘制单点激励和双点激励情形下员工集结值的变化趋势,如图3所示.

图3 单、双点激励情形各员工集结值的变化情况Fig.3 Change of aggregations of alternatives under single and double incentive points respectively

观察图3可以发现,单点激励情形下,随激励偏好系数的变化,各员工集结值的变化趋势基本一致(变化幅度略有不同),说明单点激励情形下,决策者激励偏好系数对各员工奖惩结果的影响是同方向的,即激励偏好系数的变化能够对所有员工实现同时奖励(集结值变大)或惩罚(集结值变小);双点激励时,员工2、员工3和员工5的集结值变化趋势一致,随着激励偏好系数的增加,集结值基本呈上升趋势,但员工5的上升趋势不明显,而员工1和员工4的集结值变化趋势一致,随着激励偏好系数的增加,集结值基本呈先上升再下降的趋势,说明双点激励情形下,决策者激励偏好系数的变化能够对各员工实现奖惩并行.

(c)不同激励偏好系数下员工之间集结值的对比分析

为分析激励措施的采取是否对员工起到奖惩作用,这里将不同激励偏好系数下员工的集结值与采用算术平均方法(代表无激励情形)得到的员工集结值(分别为5.60,6.23,5.80,5.42,6.23)进行比较分析,见图4.

图4 单、双点激励情形员工之间集结值的对比图Fig.4 Comparison of aggregations of alternatives under single and double incentive points respectively

观察图4可以得出,比较Ip=0.5的集结值和平均集结值,发现无论单点激励还是双点激励,Ip=0.5时各员工的集结值均大于其平均集结值,且集结值之间的差异变大(参照表4和上述平均集结值),原因是有序分位加权集结算子中分位权重加和不等于1,即相比于平均集结方法,有序分位加权集结算子中Ip=0.5时分位权重之和的增加拉大了集结值及其差异,因而本文将Ip=0.5的情形定义为“无方向的均等激励”而非“无激励”;单点激励时,无论在何种激励偏好系数下,员工集结值均大于平均集结值,而双点激励时,存在员工集结值小于平均集结值的情形,说明单点激励多体现的是对员工的奖励,而双点激励是对员工的奖惩并行;当激励偏好系数Ip≥0.3时,员工之间的集结值变化趋势基本一致,但随着激励偏好系数的增加,各员工集结值之间的变化幅度也有所增大,而激励偏好系数较小时(Ip=0.1,0.2),员工之间的集结值变化趋势与Ip≥0.3时的差异较大,表明负激励且激励程度越大时,能够对员工之间的排序产生影响,而正激励虽然对员工之间排序影响不大,却能够拉大员工集结值之间的差异.

综上可知,在本文给出的算例中,建议选用正向双点激励(且激励偏好系数应尽可能大)的方式对被评价对象进行激励,因为这种激励方式不仅能够实现对被评价对象的奖惩并重,又能够通过奖惩凸显被评价对象之间的差异.上述求解理想激励点的方式适用于以下两种情形:一是决策者能够给出激励方向和激励程度的判断,却不能明确把握激励位置;二是决策者意图通过分段激励最大程度地实现奖惩并拉大被评价对象之间的差异.

6 结束语

本文面向管理决策中的激励问题,提出了有序分位加权集结算子这一新的集结方式.该集结方法具有以下特点:1)以分布分位数的方式衡量被评价对象的相对发展程度;2)决策者通过提供激励点的方式实现对被评价对象的分段激励,这种激励方式能够更加细腻地刻画被评价对象之间的发展差异;3)分位权重的设置扩大了权重系数的取值范围,从而提升了奖励或惩罚的幅度.进一步将研究有序分位加权集结算子在动态奖惩评价问题中的集结理论及应用.