考虑媒体效应的微博网络热点事件舆论演化模型

刘 泉荣莉莉颜克胜

(1.大连理工大学系统工程研究所,辽宁大连116024；2.南阳师范学院计算机与信息技术学院,河南南阳473061)

1 引 言

近年来,Twitter、新浪微博等微博应用在人们生活和交流中占据越来越重要的地位.以新浪微博为例,2014年12月的月活跃用户数为1.757亿个,日均活跃用户数为8 060万个[1].微博网络中,较低的信息发布和传播门槛,多样的信息内容形式(可以包含文字、网页和视频等),以及病毒式的信息传播机制,使得某些网络事件参与群体急剧增多,被迅速放大为网络热点,短时间内演化成广泛关注的焦点.作为网络舆论热点事件首曝媒介,在2013年微博首曝事件的比例为15%[2],微博网络在网络舆论演化中的地位越来越突出.2014年,近四成网络舆论热点事件得到涉事主体回应,回应方式以接受记者采访最多,通过官方网站及微博等网络形式回应的涨幅明显[3].这说明,网络热点事件的舆论受到网民、媒体和涉事主体等多方面的影响.因此,研究媒体在微博网络舆论中的影响作用,为了有效应对和引导微博网络中的舆论,提高涉事主体的舆情应对能力,具有非常重要的意义.

当前,关于网络舆论的定量研究以建立舆论传播动力学模型为主,通过仿真研究舆论涌现的规律.依据观点的类型,舆论传播动力学模型主要分为:离散观点模型和连续观点模型.经典的二维离散观点模型主要是Sznajd模型[4],经典的连续观点模型主要是Deffuant有界信任模型[5]和H-K有界信任模型[6].有界信任模型的核心思想是个体同观点差异在一定阈值(信任水平)内的邻居交流观点.目前,对连续观点模型的扩展主要集中在如下方面:1)对个体观点受直接邻居的影响进行扩展,有文献考虑了最近邻和次近邻的影响[7]和更深层级邻居节点的影响[8],以及随机节点的影响[9,10]等;2)考虑外部环境的影响作用,有文献引入了全局性周期扰动[11],考虑排斥交互的影响[12],以及节点可以随机改变自身观点的影响[13]等;3)关于网络结构上的扩展,已有研究研究者分析了分层正式组织[14]、有向小世界[15]、有向自适应网络[16]、交互网络[17]和多层耦合网络中的观点演化[18,19]、考虑社团结构的影响[20]等;4)考虑节点异质性的研究[21-23]等.在上述相关的舆论动力学研究之外,目前运用超网络进行网络舆情的研究正在成为新的研究热点,其中以刘怡君等提出的包含社交子网、环境子网、心理子网和观点子网的网络舆论超网络模型为代表[24,25].文献[26]和文献[27]对意见动力学的研究进行了详细的综述.刘怡君等[28]分别从数学、物理学、复杂性科学和社会物理学四个视角,对舆论动力学模型进行了全面的综述。

但是,上述舆论演化模型均是随机选择两个节点或多个邻居进行观点交互,而微博网络中观点具有转发传播的特点,故将上述模型直接应用到微博网络中还有一定的局限性.在微博网络中,用户发布或转发的微博将向其粉丝进行广播,粉丝可以获得所关注人的评论;而如果用户不转发该条微博,其粉丝将不能得到关于该信息的评论.鉴于以上分析,本文针对目前舆论动力学中较少研究外部媒体影响的问题,考虑媒体因素和微博网络中转发用户才能影响其粉丝观点的特性,以及节点信任界限异质性对舆论的影响,构建了微博网络中考虑媒体效应的舆论演化模型,研究影响微博网络中舆论演化的主要因素.最后,在一个真实的Twitter网络上对模型进行了仿真分析,重点考察转发概率、媒体效应和节点信任界限异质性等对舆论演化的影响.研究结果表明:存在媒体影响时,个体对媒体观点的采纳幅度越大,媒体引导的效果越好;群体观点易于改变的舆论热点事件中,媒体首次报道时间越晚,媒体的引导效果越好.本文的结论同文献[29]中“政府应慎重发表言论”的结果相吻合.同时,本文的仿真实验结果也同实例相符合,说明了本文模型的正确性和适用性.本文在微博网络的舆论演化中考虑了外部媒体的影响作用,根据网络结构考虑了节点信任界限的异质性和信息传播过程,构建了微博网络中的舆论演化模型,研究结果可为微博网络中的舆论引导与控制提供理论支持.

2 考虑媒体效应的微博网络舆论演化模型

借鉴经典的传染病模型—–SIR模型,结合微博网络中信息和观点传播的特点,本文把网络中的节点状态分为三类:未激活态节点(S态)、激活态节点(I态)、失去兴趣节点(R态).未激活态节点表示尚未接收到消息,但可以接收消息的节点,类似于SIR模型中的S态.激活态节点表示该节点接收到来自其邻居节点的消息,并转发该消息,类似于SIR模型中的I态.失去兴趣节点表示该节点失去传播该消息的兴趣或能力,类似SIR模型中的R态(本文假设,失去兴趣节点虽不再转发消息,但也可以受媒体影响).

微博平台出现后,新媒体正悄然改变着热点事件的传播路径:新媒体引发热点事件—传统媒体落地—网络媒体转载[30].微博中信息发布的零门槛,促使其逐渐成为热点事件的发源地.当事件在微博中传播到一定规模时,迅速得到媒体的关注,逐渐形成热点.为表述方便,本文把传统媒体报道、网络媒体报道、当事人回应和官方新闻发布会等统称为媒体影响.下文把媒体观点定义为Op.本文引用文献[11]的思想,把媒体影响作为对全局观点的周期性扰动,引入到观点的交互过程中来,进而分析其在微博网络中舆论演化的作用.

对于模型,做如下假设:1)假设网络中有N个个体,初始时刻每个个体的观点值随机的分布在观点空间xi(0)∈[0,1].2)假设节点传播微博信息时均附上自己的观点,即用户转发微博时附带上自己的评论(某些节点在转发时可能没附上评论,为计算简单,本模型对此进行了简化处理;同时,模型不考虑微博中评论功能带来的观点传播).有向边的起点为源节点,有向边的终点为目的节点.下文为描述方便,定义源节点为目的节点的直接邻居.

节点的观点倾向和状态采用异步更新的方式进行.在每一个时步t,对所有节点的状态和观点倾向更新一次.在每一时刻随机抽取一个节点,根据其上一时步的状态和观点倾向、邻居节点的状态和观点倾向来决定该时步的状态和观点倾向,当所有节点更新一遍时,该时步结束.具体地,节点状态和观点倾向的更新遵循如下规则:

1)如果在t时步,节点i处在未激活态,有β的概率退出演化,在t+1时刻变为免疫态,否则判断其邻居中激活态节点数量ΔI,如果ΔI≥1,则其在t+1时刻有λ的概率变为激活态;i在t+1时刻的观点改变公式为

其中Ni(t)={j|Statej(t)=1且|xj(t)-xi(t)|＜di}是节点i的信任界限内且为激活态的邻居集.|Ni(t)|表示集合Ni(t)的基数.Statej(t)=1表示节点j在t时刻为激活态.α表示个体i上一时步观点在该时步观点中所占权重,本文中取α=1/(1+|Ni(t)|),即权重相等.

为节点i的信任界限,表示对自己观点的不确定性或者思想的开放性等,其中ki表示节点i的出度,kmax表示所有节点中出度的最大值.

式(2)说明出度大的节点具有较小的信任界限,出度小的节点具有较大的信任界限.值得注意的是,每个时步未激活态节点并不是采纳信任界限内的所有邻居节点的观点,而是仅仅采纳信任界限内的激活态邻居的观点.如果取d1=d2=···=dn,并且去掉Statej(t)=1的限制,本文改进模型退化为经典的H-K模型.

2)如果在t时步,节点i处在激活态,则在t+1时刻,有β的概率失去对该消息的兴趣,退出演化,变为免疫态,否则变为未激活态;i在t+1时刻的观点同t时刻保持一致.

3)如果在t时步,节点i处在免疫态,则节点i退出t+1及以后时步的演化,一直保持免疫态,并且观点跟随上一时刻不变.

4)在第T个时步,所有个体有q的概率会同时受到媒体的影响,其观点受媒体影响的改变公式为

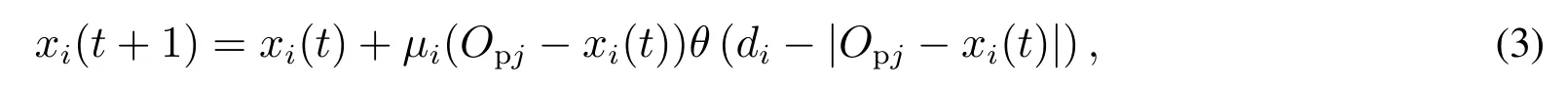
其中Opj表示第j个媒体的观点,Opj∈[0,1];µi为收敛参数,表示个体i接收媒体观点的幅度,µi∈[-1,1].这里µi的值取决于媒体观点的可信性、论据的详实程度等方面.假设q=0.5,θ(y)函数表示个体仅与媒体观点之差在其信任界限之内时才进行观点交互,即

值得注意的是,由于上述的媒体作用,观点演化规则式(3)可能导致个体的观点超出区间[0,1],为了保持xi(t)∈[0,1],附加如下的强制条件

3 仿真分析

为分析微博网络中的观点传播和舆论演化规律,本文对提出的模型在一个真实的Twitter网络上进行了蒙特卡洛仿真.从文献[31]的Twitter网络数据集中,采用滚雪球的方法和宽度优先的策略抽取了由1 550个节点,33 732条有向边所构成的子网络,平均出度为21.76,平均聚类系数为0.372,平均路径长度为3.466,网络的出度分布如图1所示,Twitter网络为有向网络.目前已有的实测研究表明,新浪微博和Twitter网络具有小世界和无标度特性,出度和入度均服从幂率分布[32-35].这说明本文抽取的子网络符合微博网络的拓扑结构特征.本文中,节点的信任界限根据式(2)计算,信任界限的取值分布如图2所示.从图2中可以发现,Twitter网络中60%的节点信任界限取值在区间[0.9,1]之间,这说明由于网络中节点的出度呈幂律分布,使大多数节点的信任界限取值较大,仅有极少数节点的信任界限取值较小.这对目前的部分网络热点事件来说,无疑是符合现实情况的.

为讨论网络结构对观点演化的影响,本文又在有向无标度网络上进行了仿真研究.用Price有向网络模型[36]来构建有向无标度网络.Price有向网络模型的构造算法为:1)初始网络为m0个相互连接的节点,在每个时间步t增加一个新的节点i,同时生成m条由m个已存节点指向新节点i的有向边.2)已存节点被选择的概率依赖于其出度.理论解析表明Price有向网络模型的出度服从幂率.这里产生一条已存节点指向新节点的有向边对应于一个新注册用户会收听一些老用户.仿真中m0=10,m=10,Price网络结点个数为1 000,平均出度为9.945,平均聚类系数为0.032,平均路径长度为3.197,从图1中可以看出网络的出度服从幂律分布.Price网络和Twitter实际网络不同之处在于,Price网络中节点的入度均为10,Twitter网络中节点出度为幂律分布.

图1 网络节点出度分布图Fig.1 Out-degree distribution of network nodes

图2 节点信任界限分布图Fig.2 The distribution of node confidence limit

本文运用终态观点均值M和观点标准差σx[19]作为参数衡量网络舆论的总体情况,

其中N表示节点总数,xi(t)表示节点i在t时刻的观点,(t)表示t时刻观点平均值.观点标准差σx值越大,表示观点越无序;当达到一致性的公共舆论时,σx的值趋近于零.

仿真流程主要分为如下部分:首先,在没有媒体作用下,考察观点传播过程的影响作用;其次,重点研究媒体的作用,并结合观点传播过程进行分析.仿真步数为100个时步,每个参数上的结果取100次独立实验的平均值,以减小交互过程中随机性的影响.仿真中随机选择一个节点作为初始节点为I态,其余节点为S态,初始节点的观点值取0.8.

3.1 观点传播过程的影响作用

在t=0时刻,每个节点观点xi(0)均匀分布在区间[0,1]之内.图3(a)中,当转发概率比较小时,终态观点标准差σx较大,此时网络中很难形成一致性的舆论;随着转发概率的增大,终态观点标准差σx逐渐减小,直至趋于稳定值.当转发概率增大到一定程度时,σx值稳定在0.15左右(Twitter网络),近似达到一致性舆论,具体的观点分布见图4.随着转发概率的增大,观点传播的范围逐渐增大,节点之间的观点交互次数也逐渐增多,此时网络中的观点逐渐趋同.当转发概率λ增大到一定程度时,观点标准差σx不再变化,这说明交互次数达到一定程度时,对观点演化的影响作用逐渐减小.本文也对比了初始节点出度不同的影响,如图3(a)所示.当初始节点的出度较小时(k0=8),σx值也随着转发概率的增大而减小,但是减小的速度较快,形成稳态时需要的转发概率值也较大;当k0=49,100时,曲线较为相似,这说明当初始节点出度足够大时,初始节点的不同造成的影响较为有限.这说明对于有较大吸引力的话题,无论是谁最先发布的,都能够引起一致性的舆论,达成系统共识;对于吸引力较小的话题,发布者的影响力就较为关键,仅仅影响力较大的发布者才可能形成较为一直性的舆论.

图3 转发概率λ与终态观点标准差σx之间的关系Fig.3 The relationship between the forwarding probability λ and the standard deviation of the final view σx

本文也对比了不同网络结构的影响,在Twitter网络和Price有向网络中,两者总体的曲线趋势相同,仅在初始节点出度较小时,曲线有差别,这是由两个网络的连通性不同造成的.在Twitter网络上,不同的初始节点所造成的终态观点标准差σx的差异较小,这说明由于网络的连通性较好,网络舆论逐渐呈现去中心化的趋势,这符合实际微博网络中舆论的特点.在两个网络中,当k0=49,100时,随着λ增至0.4,观点标准差σx的稳定值在Price有向网络中反而大于Twitter网络,是由于Price有向网络中有更多的大信任界限节点(见图2),并且Twitter网络中有部分节点入度为零,其观点始终未发生变化,而根据网络构建规则,Price有向网络中无入度为零的节点.

图3(b)中,比较了节点信任界限同质性和异质性之间的差异.取同质性时,随着信任界限取值的增大,终态时观点逐渐趋同,观点标准差σx逐渐减小,这同经典H-K模型相吻合.但值得注意的是,即使所有节点信任界限取值较大时(例如di=0.8时),本文模型也不能形成完全一致性舆论(σx=0),这与经典H-K模型不同.在无媒体影响时,本文模型不能形成完全一致性舆论,这可能是三方面因素造成的,一是由于模型中节点存在有界信任的特点,有些信任界限较小的节点改变自己观点的机会较小,甚至不改变观点(例如di=0时);二是在信息传播过程中,并不是所有的节点都能进行观点交互,即某些节点从始至终未参与到舆论讨论中来;三是由于免疫概率β的存在,某些节点在讨论的途中失去兴趣,观点不再改变.本文的异质性信任界限取值方法与同质性信任界限di=0.5所得到的结果相似,但是本文的异质性信任界限值在区间[0,0.5]之内的比例为2.4%.这说明对出度较大的节点赋予较小的信任界限,对舆论演化结果产生了显著的影响.

针对Twitter网络中,个体观点随时间的演化做了具体分析,如图4所示.由于节点个数较多,为了图示清楚直观,本文把节点观点分为5个区间[0,0.2),[0.2,0.4),[0.4,0.6),[0.6,0.8),[0.8,1],分别在转发概率λ=0.05,0.1,0.3,0.6四种情形下分析了随时步落在各个区间的节点数量变化情况.

图4 随时间变化的各区间观点数量,Twitter网络,初始节点为k0=49Fig.4 Time evolution of opinion number with different spreading rate,Twitter network,the initial node k0=49

从图4(a)中可以看出,当转发概率λ=0.05时,五个区间上的观点比例差别不大,均集中在0.2左右;图4(b)中,随着转发概率λ的增加(λ=0.1时),区间[0.4,0.6)内的观点数量急剧增加,区间[0,0.2)和[0.8,1]内的观点数量逐渐减少;当转发概率λ=0.3,0.6时,两者保持了相同的曲线趋势,同λ=0.1相比,区间[0,0.2)和[0.8,1]内的观点比例更少,均在5%左右.这说明随着转发概率的增大,观点交互次数的增多,系统中的极端观点越来越少,大部分节点的观点集中在中间部分,这种观点的演化趋势同经典H-K模型相吻合.

3.2 媒体的影响作用

在本节的仿真中,主要考察媒体因素的影响,仅在Twitter网络中进行了仿真,设定参数λ=0.3,k0=49,β=0.05.假设T=T0+5h,h=0,1,2,...,9时步,节点同时与媒体信息进行观点交互,T0为媒体首次报道时间,媒体观点为OP=0.8.为简单起见,本文仿真中将所有媒体的观点统一设置为OP,但是也可以将本文模型推广到媒体观点不同的情况.

图5为不同的媒体影响次数m下,终态观点均值M与µ的关系图.本文中µ为收敛参数,表示个体对媒体观点的采纳程度,同媒体观点的说服力有关.在图5(a)中,t=0时刻,90%的节点观点均匀分布在[0,0.2]内,剩余10%节点的观点均匀分布在[0.2,1]内,可得系统初始观点平均值M0=0.15;在图5(b)中,t=0时刻,每个节点观点在[0,1]之间服从均匀分布,系统初始观点平均值M0=0.5.从图5能够看出,对于固定的媒体影响次数m,随着µ值的增加,终态观点均值M增大.对于固定的µ值,当µ＞0时,随着媒体影响次数m的增加,终态观点均值M增大;µ＜0时,随着媒体影响次数m的增加,终态观点均值M减小.对比图5(a)和图5(b)时可以发现,两者在总体上有着相同的变化趋势,在细节上可以发现,相同的m和µ值下,初始时观点均值大时,终态M值也较大.图5表明,在相同的影响次数下,媒体的论据越详实,观点说服力越强,才越能有力的引导舆论;当不知道事情真相,论据含糊时,不要过多的得出结论,谨防说的越多,错的越多的情况发生,没有起到正面的效果,反而引起公众的质疑.上述结论同文献[29]的结果吻合,其认为“当非常规突发事件引发公共恐慌时,政府应该慎重发表言论,注重自身的公众形象,并在应急政策准备充分情况下,尽快公布事件真相”.值得注意的是,图5中还可以发现,即使提供了有力的论据,也需要经过多次影响,才能达到预设的引导目标.

图5 有媒体时,终态观点均值M与µ的函数关系,OP=0.8Fig.5 The final magnetization M as the function ofµ,when there is an influence of media,OP=0.8

由于观点平均值并不能完全反映观点的有序性,本文又使用观点标准差σx来辅助观测终态时的观点一致性,如图6所示.从图6(a)可以看出,对于固定的µ值,当µ＞0时,σx值随着m值的增大,先增大后减小;σx的最大值出现在m=3,µ=1时.这说明媒体观点同公众初始观点相左时,经过三次左右的宣传,舆论达到最混乱,随着影响次数的增多舆论逐渐趋于一致,这同现实生活中公众对新事物的认知过程相一致.对于一个新生事物、新产品或新技术,公众的认知同样是从未知、恐惧到混乱,再到一致和接受的过程.对比图3(a)与图6(b)可以发现,媒体的影响作用是十分显著的,当媒体宣传起正向作用时,媒体可以促使系统的观点更为一致.

图6 有媒体影响时,终态观点标准差σx与µ的关系,OP=0.8Fig.6 The standard deviation of final opinion σxas the function ofµ,when there is an influence of media,OP=0.8

通过调节系统初始观点平均值,进一步观测初始观点分布对系统观点演化的影响.从图7中可以发现,在初始观点分布不同时,达到相同的M值,M0=0.15时比M0=0.5均需要多花费4次左右的宣传;对于固定的m值,M值随着M0的增大而增大,当m=10时,M值趋同.横向比较可以看出,初始观点分布的不同,使媒体需要提供不同的影响次数才能达到相同的宣传效果.值得注意的是,即使初始时社会舆论同媒体观点相差较大,经过多次的引导(m≥10),同样可以达到预设的效果.

图7 终态观点均值M和媒体影响次数m之间的关系Fig.7 The relationship between the mean of the final state view point M and the number of media influence m

图8 不同的媒体首次报道时间下,媒体影响次数m与终态观点均值M和观点标准差σx的关系Fig.8 The relationship between the number of media influence m and the mean of the final state view point M and the standard deviation of final opinion σxunder different media first reported time

本文也分析了媒体首次报道时间对终态观点均值M和观点标准差σx的影响.图8(a)中,在初始平均观点同媒体观点差异较大时(M0=0.15,OP=0.8),固定m值时,终态观点均值M随着T0增加而增加,当T0达到一定程度时,其影响作用变得不再明显.图8(b)中,固定m值时,观点标准差σx随着T0增大而增大,当T0增大一定程度时,观点标准差σx保持不变;T0＞25时,观点标准差σx的峰值提前至m=3处,说明媒体首次报道时间越晚,将导致观点混乱的时间提前.从图8可以发现一个有趣的现象,随着T0增大,终态观点均值M和观点标准差σx同时增大,这说明系统观点平均值增大的同时,系统中观点却更加混乱.

本文对比了终态时节点的观点分布,如图9所示.

图9 终态节点观点分布比例图Fig.9 Distribution proportion diagram of final state node point of view

图9表明,造成上述状况的原因是,T0=25,50时,70%以上的节点观点集中在[0.6,0.8]区间内,而在[0,0.2]区间的数量多于T0=5时,这造成了观点标准差较大.当T0较大时,系统中已经初步形成较为统一的观点,此时同媒体观点交互,由于信任界限的存在,少部分极端节点不再采纳媒体观点,但绝大部分节点观点向媒体观点靠近,这说明随着初次介入时间推迟,反而取得了更好的宣传效果,这一结论与人们的常识相反.由于本文对于信任界限的设置方式,绝大部分节点具有较大的信任界限,故对媒体观点的采纳影响较小,这说明本文的结论较适用于部分群体观点易于改变的舆论热点事件中.对于群体观点难以改变的网络群体性事件,媒体介入的越晚,其起到的作用则将可能有所不同.

4 实例验证

为研究真实热点事件中网络舆论的演化过程和演变规律,针对“成都女司机变道被暴打事件”随机从新浪微博中分两个时间点(第一个时间点为5月3日,第二个时间点为5月5日)分别抓取了300条消息,然后对这些数据进行了观点分析.为保证准确率,对微博消息的观点分类采取了人工判别方法[37],三人交叉标注消息观点,至少两人标注结果一致或相近时,认为该结果正确.

实例简介:2015–05–03,成都商报官方微博发布消息“娇子立交发生暴力打人事件”,称成都市一名男性司机逼停一名女性司机后,将其拉下车痛殴.该报道迅速引起众多网络媒体和传统媒体报道和转发,一时引起网络热议.05–04晚,该男司机行车记录仪拍下的视频被多个媒体曝光,显示女司机多次变道在先,别车险造成事故.

根据从新浪微博平台中抽取的5月3日的300条评论作为样本,得到了该事件的初始网络舆情分布,如 图10(a)所示.从图10(a)中可以看出,主要的网络观点为“反对暴力,无论谁有过错,男司机都不应该打人”.如果假设最极端观点“完全是女司机过错”的观点值为1,“完全是男司机过错”的观点值为0.为图形表示方便,将实际存在观点归结为四类:“男司机过错”、“女司机过错”、“双方均有过错”、“无论双方谁有过错,不该打女人”.采用人工标注的观点值,根据式(6),可计算得此时该事件的初始平均观点为0.369.

图10 “成都女司机被打事件”观点分布图Fig.10 The viewpoint distribution diagram of“Chengdu women driver beaten event”

根据5月5日的300条评论作为样本,得到了该事件的终态网络舆情分布,如图10(b)所示.由于媒体公布的视频可信程度较高,造成了网民观点的急剧转变,网络中主流观点变为“女司机该打”.此时,存在的观点可以归纳为三类:“女司机该打”、“男司机该罚”、“双方均有过错”.根据式(6),可计算得终态观点均值为0.809.从该实例可以看出,在媒体的不断报道之下,网络舆论呈现极大多数支持男司机的局面,形成了网络意见的近似一致状态.此时网络中的观点分布情形对应于本文仿真实验图5和图6中µ=1,m＞5时的结果,仿真实验表明,在论据充分时,经过多次报道可以形成群体意见的基本趋于一致.从以上的对比可以看出,本文的仿真实验结果与实际统计数据基本吻合,说明了本文模型的正确性.

5 结束语

本文针对微博网络中只有转发节点才能影响其邻居节点观点的特性,并着重考虑媒体影响以及节点信任界限异质性对舆论的影响,提出了一种微博网络中考虑媒体效应的舆论演化模型,研究了影响微博网络中舆论演化的一些主要因素.研究结果表明:无外部影响时,对于极具吸引力的话题,微博网络中有较大概率形成近似一致性舆论;有媒体影响时,媒体论据的说服力决定着媒体宣传的效果;初始观点分布影响着媒体需要宣传的次数,同时媒体首次报道时间也影响着宣传的效果.

本文提出的模型能够较好的反映微博网络中舆论演化的真实情况,可以还原诸多的舆论现象,如在媒体影响下的舆论反转等.知名博主在微博网络中具有较强的影响力和话语权,能够较大的影响网络中舆论的发展.普通微博用户只有在发布一些具有吸引力的话题时,才可能在网络中形成较一致性的舆论.当社会中的个体普遍具有较高的信任界限时,媒体介入时间越早并非总能取得较好的引导效果.媒体观点需要有力的论据作为支撑,否则只能适得其反,同时,即使提供了有力的证据,也需要多次宣传,才能达到预设的引导目标.本文的工作有助于深入剖析微博网络中的舆论演化规律,为进一步研究网络群体性事件在微博网络中的舆情演化和预警提供理论基础.本文研究的考虑媒体效应的微博网络观点演化机制,具有一般性,可以推广应用到其他研究领域,例如,能够对研究新技术的传播过程,新产品的广告投放策略等提供有益的补充.本文模型主要适用于个体观点易于改变的网络热点事件,未来的工作是研究更多类型事件中舆论的特点,同时研究媒体观点变化时舆论的演化规律,为微博网络中的舆论控制提供具体的建议.