公共危机双层网络伪信息扩散与免疫阈值研究

朱晓霞,刘萌萌,沈羽翯,陆君安

(1.燕山大学经济管理学院,河北秦皇岛066004;2.国家无线电监测中心,北京100037;3.武汉大学数学与统计学院,湖北武汉430072)

1 引 言

公共危机作为突发性的群体危机事件对人们的日常生产及生活带来了极大的不良影响,而由于谣言等伪信息扩散引起的公共危机事件随着时代的发展占据着越来越高的比例.日本核辐射引发的“抢盐”事件,关于艾滋病“滴血食物传播病毒”事件,地震谣言令山西数百万人街头“避难”等公共危机事件均由相关伪信息的谣传而引发.谣言等伪信息带来的严重后果使得相关部门越来越重视伪信息扩散在公共危机中的负面作用,因此研究伪信息的扩散特性及免疫阈值对伪信息扩散过程的控制与干预具有重要的理论与实践意义.

近年来,信息时代的发展给予了伪信息更多的传播渠道,使得伪信息扩散所基于的网络日趋复杂化.复杂网络模型能够在一定程度上模拟现实社会中的部分网络,一时间以复杂网络[1-3]为基础研究谣言等伪信息扩散受到了较多研究者的认可.从伪信息扩散研究所基于的网络来看,可分为单层网络与双层及多层复杂网络.

以单层网络为载体,有关谣言等伪信息研究的重要研究内容之一是伪信息扩散的模型.Daley等[4]最早利用D-K模型研究谣言的扩散,Trpevski等[5]研究了基于传染病SIS模型的两种谣言扩散机制,Hosseini等[6]利用考虑了无标度网络结构多样性的传染病模型来研究谣言信息的传播动力学.杨孟等[7]探究了传染病模型在传播过程中的稳定性.在研究的过程中,众多学者不断对信息扩散模型进行改进,使其更符合实际的扩散特性.如Wang等[8]研究了复杂网络中增加了信任机制的扩散模型,王筱莉等[9]探究了无标度网络中遗忘率变化的谣言传播模型等.在伪信息扩散模型研究的基础上,根据不同的复杂网络特性,提出了三种基本的免疫策略,即随机免疫、目标免疫与熟人免疫[10],广泛应用于基于复杂网络的免疫研究中.但以上研究大都基于随机网络,无标度网络等单层的独立网络,并未考虑到该网络与其他网络之间的相互作用.而实际中的网络却大多不是单一存在的网络结构,而是与一个或多个网络之间具有一定的相互关系.

因此,随着对谣言等伪信息扩散研究的进一步深入,之前有关谣言等伪信息基于独立单层社交网络的研究在面对当前的信息环境时,越来越显示出了其片面性,以双层及多层网络为基础的研究逐渐引起了国内外学者的重视.从相互连接的网络到相互叠加的网络,Wang等[11]针对简单的相互连接网络中的传播进行了研究,其中假设了节点之间一对一的连接.Zhao等[12]研究了双层叠加网络的传播阈值及爆发规模,并探究了度相关对传播阈值及爆发规模的影响作用.Dickison等[13]研究了强耦合与弱耦合网络中流行的传播.

在以上关于双层网络伪信息传播的研究中,为便于研究,通常假设双层网络之间个体的相互联系数量,而实际中个体间相互联系的数量是不固定的,因此该方法难以拟合实际情形.随着研究的深入,基于实际问题的谣言扩散研究将是今后的研究重点之一.此外,由于伪信息的扩散研究需最终落脚于伪信息免疫,而目前有关伪信息免疫中双层网络的免疫研究相对较少,双层网络免疫阈值如何确定成为双层网络免疫研究的重要基础.由此,本文将探究实际中双层网络的扩散阈值公式及免疫策略下相应的免疫阈值.

基于当前的研究成果,本文运用SIR模型确定网络中个体间的交互规则,利用计算机仿真工具建立了不同地区人群构成的双层人际关系网络,该双层网络之间随机连接,打破了简单的一对一连接限制,更符合实际情况中地区间人们的相互联系特征.进而通过推导得出该双层网络的传播阈值计算公式,得到阈值曲线;并以此为基础,根据随机免疫策略,探究了双层网络间的相互联系对伪信息免疫的影响作用.发现双层网络间的相互关系对伪信息的免疫在不同情况下作用方向不同:免疫单一网络,对伪信息扩散情形具有抑制作用,但不存在免疫阈值.二者都免疫,对伪信息扩散具有促进作用,免疫阈值增大;最终,根据双层网络联系,推导得出了综合免疫下的双层网络免疫阈值.

2 公共危机中双层网络的伪信息扩散机制

2.1 公共危机伪信息扩散的双层网络结构

由于现实中的网络并不是孤立存在的单层网络,各层网络之间都有着或多或少的联系.当前在线社交网络中信息传播越来越成为社会关注的热点,但线下社交网络中的伪信息扩散仍不容忽视,一些在网络中禁止讨论的话题仍然可以通过线下的渠道进行扩散.就某地区单独而言,有自己实际的人际社交网络,其与附近地区的人之间也存在一定的联系.因此,本文以具有相互联系的双层网络模拟现实情形中两个相互联系的地区,进而研究公共危机伪信息的扩散与免疫.

双层网络拓扑结构如图1所示.双层网络具有如下特性:整个网络由子网1与子网2,每层网络具有独立的度分布,两层网络之间的节点随机进行连接,其中一层网络中的节点与另一层网络节点的连接数不固定,模拟现实生活中人际关系多少参差不齐的情况,且两种不同的网络中伪信息扩散的速率也存在着一定的差异.

由于伪信息扩散与传染病蔓延具有极大的相似性,因此本文利用SIR(susceptible-infected-recovered)经典的传染病模型设置伪信息的扩散规则,将人群分为三种类型,S(不知情者),I(传播者),R(免疫者).在子网1中,伪信息的传播速率为α,即处于S状态的人接触到处于I态的人之后将以概率α转化为I态.处于I态的人以σ的概率转化为R态.此时,子网1中的有效传播率为λ1=α/σ.子网2中类似,伪信息的传播速率为β,有效传播率为λ2=β/σ.

2.2 公共危机中双层网络伪信息扩散的阈值

将SIR模型与渗流理论相结合,有效传播速率对应于渗流中连接被占用的概率,即λ1,λ2表示相应子网中的边被占用的概率.伪信息扩散的过程即为接收到信息的节点群的形成过程,那么随机选择子网1(或子网2)中的一条边,沿着该边而得到的节点群的规模的生成函数[12,14]如下

其中x为构造生成函数时加入的形式变量;k表示节点在整个网络中的度;pi(k)表示子网i中随机选取的节点度为k的概率;ki表示随机选择的子网i的节点在子网i中的度;ki→j表示随机选择的子网i中的节点在子网j中的度;pi→j(k)表示网络间的边所连接的子网i中的节点在子网j度为k的概率;表示节点群形成过程中在子网i节点处向子网j发展的ki→j种继续下去的方式,同理;hi→j(x)为沿着网络间的一条边由子网i中的节点扩散到子网j.

最终得到的节点群的规模分布的生成函数,具体表示为

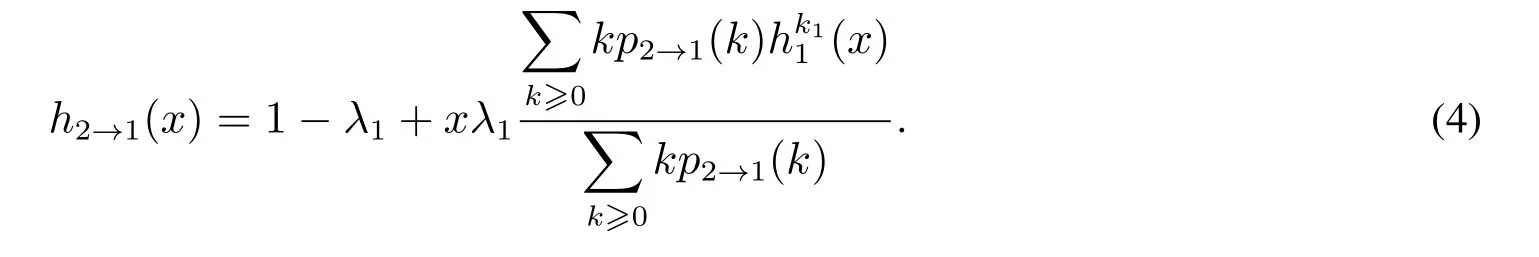
以上是由网络中随机选择的一条边而得出的爆发规模分布,但是实际中伪信息的扩散大多起始于随机选择的某个节点.因此,由一个节点引起的伪信息爆发规模可以由连接它的每条边得到的爆发规模来表示,得到以下爆发规模的生成函数

在复杂网络中经常运用生成函数来求分布函数的平均值,当x=1时,可以得出分别由子网1与子网2开始扩散的节点而得到的平均爆发规模[13,15]

令x=1,由式(1)～式(4)可得

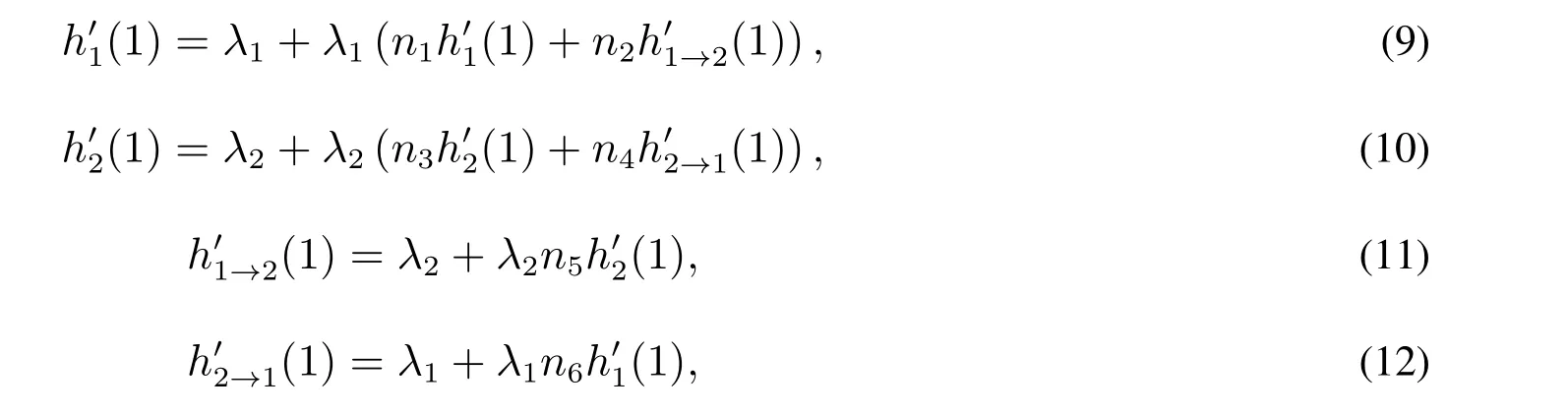
其中

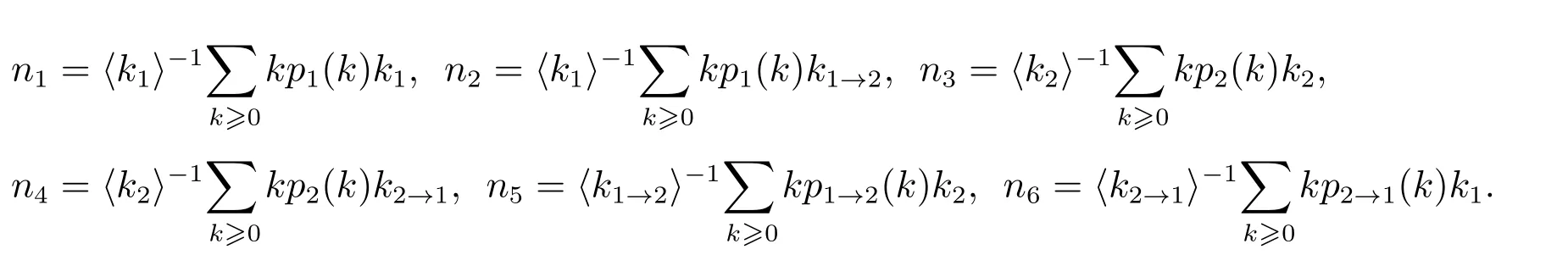
上述诸式中〈kn〉(n=1,2,1→2,2→1)代表相应的平均度.

进一步由式(9)～式(12)可得

其中

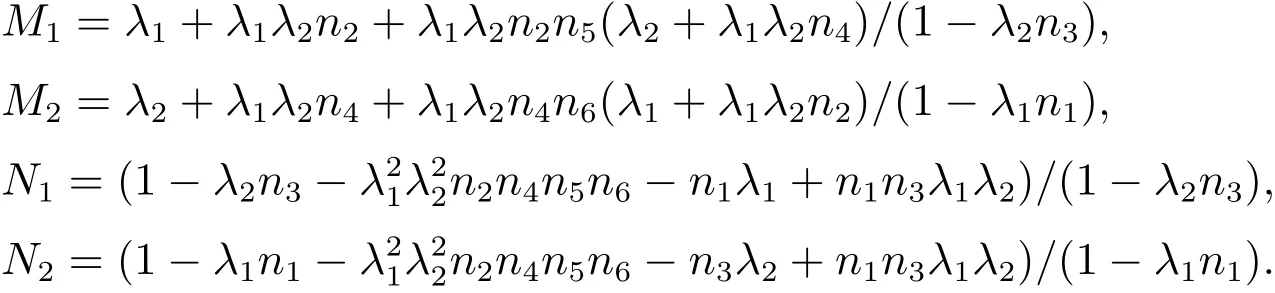
h′1(1),h′2(1)将在满足方程(14)的点处无限增大,根据式(7)与式(8)可知,此时平均爆发规模〈s1〉,〈s2〉将会趋于无限大,伪信息将会大规模爆发,该方程具体表示如下

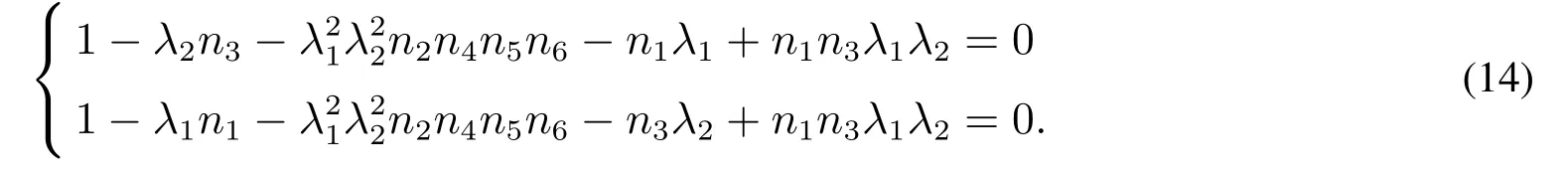
3 公共危机中双层网络的伪信息免疫

由于伪信息的扩散与传染病的传播相似,因此在伪信息中借用传染病免疫的概念,以伪信息免疫表示对伪信息扩散过程的干预及控制.下面将依据上节中伪信息的传播阈值,基于随机免疫策略,探究双层网络间的相互联系对伪信息免疫的影响作用,进而得出公共危机双层网络的伪信息免疫阈值.

3.1 双层网络参数设定

实际中,虽然人们认识的人数量具有一定差异,但线下社交网络中个体经常联系的好友数量差异较小,即个体作为网络中的节点度差异较小.由于ER随机网络中每个节点的度大致相似[10],因此本文采用两个ER随机网络模型来拟合现实中线下地区之间社交网络中的伪信息扩散.

选取ER1(1 200,3.55)与ER2(1 200,5)两个网络(除另作说明,以下所采用的网络均为该复杂网络),包含网络间连接之后的平均度设定为7与8.45.由上节的阈值计算公式得到图2所示结果:

图2 双层ER随机网络的伪信息扩散阈值Fig.2 Pseudo-information diffusion threshold value of double-layer ER random network

图2中的曲线即为由方程(14)计算得出的一系列阈值点.当伪信息扩散速率等于或超过阈值点(即图中的曲线及其上方区域)时,伪信息将会大规模爆发.因此从曲线上方区域选取一点(λ1,λ2)=(0.4,0.3),σ=0.1进行模拟仿真,进一步研究该网络中伪信息的免疫.

3.2 阻止网络间伪信息扩散的双层网络免疫阈值

复杂网络中的基本免疫策略有随机免疫,目标免疫与熟人免疫.不同的免疫策略分别对应不同的网络类型.对于随机网络,采取随机免疫方法对其进行免疫[10].当该双层网络中某一层的网络节点不能将伪信息传递给另一层网络,则该复杂网络便是两个独立的网络,根据网络特性对其分别采用相应的基本的免疫策略即可,此时为阻止伪信息的大范围扩散需免疫的个体数即为两个网络中免疫数量的和,免疫阈值即为

对双层网络进行免疫,根据上述免疫阈值公式计算得出gc=0.314,经过仿真得到如图3所示结果.其中S1,S2与I1,I2分别代表子网1与子网2中的易感者与传播者占各自网络节点的比例,R代表已免疫的节点占整个网络节点的比例,横轴T代表时间,纵轴S代表爆发规模(以下各图中均代表上述含义).此时,伪信息的扩散规模较小,波及的人群范围小,能够得到较好的控制.

图3 阻止网络间伪信息扩散的双层网络单独免疫Fig.3 Two-layered network that prevent the spread of false information between networks are individually immune

3.3 保持双层网络间伪信息扩散的单个网络免疫

保持双层网络间的伪信息扩散,针对其中一个子网进行免疫,探究其对整体爆发规模的影响,得到如图4所示结果.

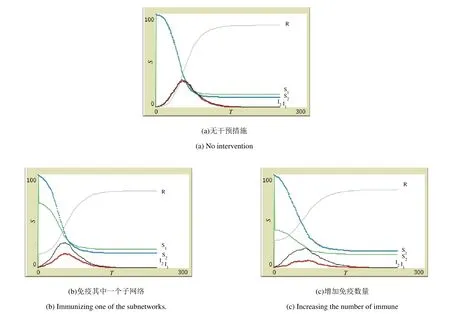
图4 免疫单个网络对爆发规模的影响Fig.4 The influence of immunization for a single network on outbreak size

如图4(b)所示,针对某一网络进行免疫,选取免疫阈值处的免疫数量,但发现免疫某一网络对总体爆发的规模的影响并不显著,增大免疫数量之后,发现二者的爆发规模同时减小(见图4(c)),因此该双层网络之间的相互联系将增大子网的免疫阈值.同时,当一个网络保持自由状态,对另外一个网络进行干预时,两个网络的爆发规模将同时减小,说明网络之间的相互作用在该情况下对伪信息扩散的规模具有一定的抑制作用.但此时整个复杂网络的爆发规模仍处于较高水平,免疫该双层网络中的某一子网不能控制伪信息的扩散,因此不存在免疫阈值.

3.4 保持网络间伪信息扩散的双层网络综合免疫阈值

如图5所示,对两个网络同时分别干预,且允许网络间的伪信息传播时,二者的爆发规模同时减小,但仍具有一定规模.因此双层网络间的相互联系对伪信息的扩散具有一定促进的作用,此时的免疫阈值并不是二者的简单相加.

本文构建的双层网络模型中,在确定总体平均度的基础上,网络间节点联系随机.因此对于两个ER随机网络而言,随机增加网络间的相互联系,对整体网络结构的影响并不显著,整个复杂网络依然为随机网络.因此,对其仍采取随机免疫策略进行免疫,免疫阈值如下

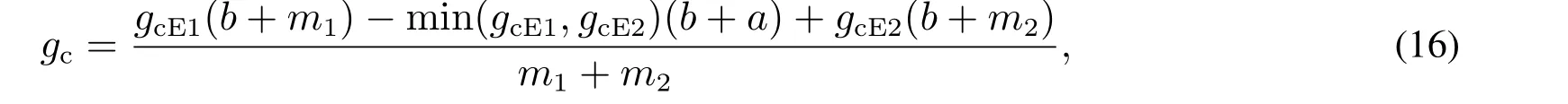
根据上述公式计算得gc=0.639.根据该复杂网络免疫阈值,对其进行免疫仿真,得到如图6所示结果.

图5 保持网络间伪信息扩散的双层网络分别免疫Fig.5 The immunization for two layered networks with information diffusion between them

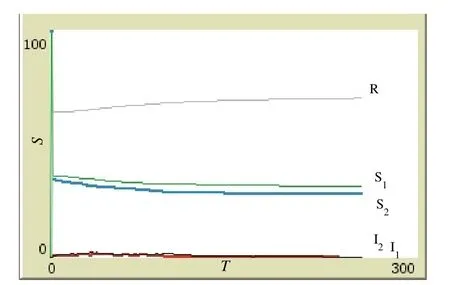
图6 双层网络综合免疫Fig.6 Integrated immunization for two-layered networks

图6表明包含双层网络之间连接的免疫阈值较单独进行免疫时增大,并不是二者的简单相加.因此在对双层及多层网络进行干预时,应充分考虑各网络层之间的关系.实际中对两个或多个地区线下伪信息扩散进行干预时,应超过对应数量的单个地区干预人数才有可能达到控制目的.

4 结束语

本文构建了公共危机中伪信息扩散的双层网络模型,得出了双层网络伪信息扩散的阈值计算公式.当扩散速率高于阈值时,伪信息将会在网络中大范围扩散,引发公共危机.因此,基于阈值计算,选取相应的扩散速率,进一步探究了该双层网络间的相互联系对伪信息免疫的影响,结果发现:对某一网络进行免疫,二者的爆发规模同时降低;对两个子网同时免疫,爆发规模进一步降低,但仍具规模.因此,双层网络间的相互联系对伪信息免疫存在双重影响作用.基于该相互联系,进一步得出了双层网络综合免疫阈值,发现免疫阈值相对于两个网络分别免疫明显增大.说明网络之间的关系越紧密对伪信息进行控制的难度便越高,需要免疫更多的人群才能对伪信息进行控制.