基于Ritz级数双驱动系统动态特性分析*

孙德鹏，李沛刚，冯显英，岳明君，杜付鑫

(山东大学 机械工程学院，济南 250061)

0 引言

在数控机床中滚珠丝杠作为进给机构的传动部件,具有高效率、高精度、低摩擦和可逆性的特点[1]。进给系统的动力学特性在控制性能中起了重要的作用。滚珠丝杠是常用的传动元件，广泛应用于进给系统中。因此，对滚珠丝杠进给系统的动态特性进行了大量的研究[2]。机床在加工时因为振动而引起的加工速度不高，加工精度不够的问题越来越严重[3]。通过对机床的模态分析可以得到机床的固有频率 、振型等固有动态特性[4]。滚珠丝杠副属于低刚度部件，在外力的作用下容易产生变形、振动和噪声，如果激振频率接近滚珠丝杠副的共振频率，系统可能会产生共振[5]。

山东大学冯显英教授多年从事微纳进给技术的研究，并提出了一种新的驱动方式“宏宏双驱动微位移进给机构”。本机构不受行程的限制，进给的持续性强，出现爬行现象的速度低。目前本技术已经应用在多个领域，例如轮胎动平衡系统，并取得了理想的效果。

目前国内外对滚珠丝杠的动态特性研究按驱动方式主要分为丝杠驱动型和螺母驱动型两种类型。对模态分析目前常用的计算方法主要有集中参数法和有限元法。国内于瀚文对双驱动微量进给伺服系统利用集中参数法进行研究。集中参数法无法准确的表示滚珠丝杠的柔性体特征,有限元法当工作台位置变化时需要重新建模设置边界条件，操作繁琐，效率低[7]。

本文针对双驱动伺服系统，采用铁木辛柯梁理论、能量守恒定律和Ritz级数建立了系统的力学模型，克服了集中参数法和有限元法的不足。并得到系统的刚度矩阵和质量矩阵的表达式。利用Matlab对数学模型运算分析，得到系统的谐振频率。

1 建立系统的数学模型

1.1 系统的工作原理

传统的驱动方式是伺服电机单驱动丝杠进行进给或者是由伺服电机驱动螺母进行进给。传统双驱动为两个伺服电机分别驱动两个滚珠丝杠。本文中双驱动系统区别于丝杠驱动和螺母驱动，双驱动系统是由两个伺服电机分别驱动丝杠和螺母，通过改变两个伺服电机的转速来实现微量进给。

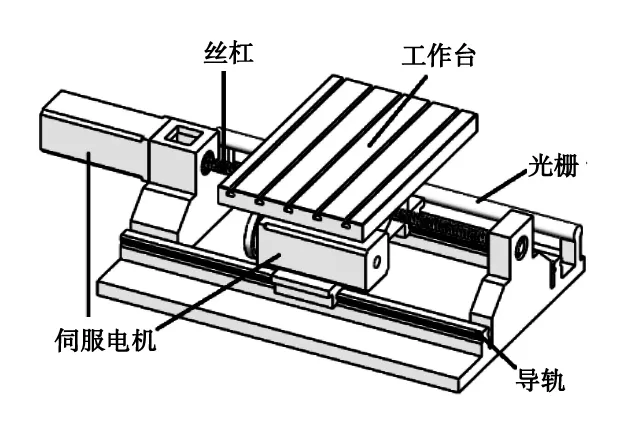
图1 双驱动试验台

1.2 数学模型

采用拉格朗日方程对如图1所示的双驱动进给传动系统模型进行数学建模。根据系统结构建立系统的动力学模型，如图2所示。

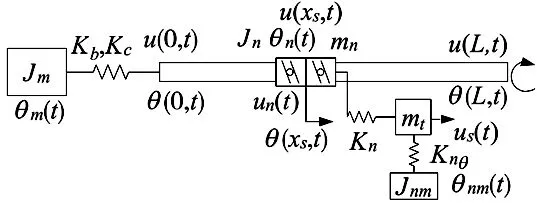
图2 双驱动滚珠丝杠副的力学模型

式中：Kb为轴承轴向刚度；Kc为联轴器扭转刚度；Knθ为螺母扭转刚度；Kn为螺母轴向刚度和螺母轴承轴向刚度的合成；i为传动比；mt为工作台质量；Jm为丝杠电机转动惯量；Jc为联轴器的转动惯量；Jnm螺母电机的转动惯量；Jn为螺母的转动惯量；L为丝杠长度。

柔性滚珠丝杠轴受扭转和轴向变形影响，其势能可写成[6]：

(1)

式中，E为弹性模量；A为滚珠丝杠的横截面积；I为丝杠的转动惯量；G为剪切模量。

滚珠丝杠轴的分布扭转和变形的动能是[6]：

(2)

式中，ρ为丝杠的密度。

根据力学模型分别建立整体系统的势能和动能的表达式：

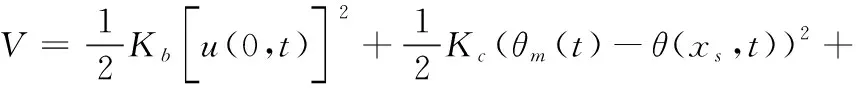
(3)

(4)

i(θn-θxs)+xs=xn

(5)

2 Ritz级数展开

Ritz法是由瑞士的著名数学家Walter Ritz提出，通过有限的级数展开近似求u(x,t)的连续变形[9]。其本质是利用级数展开式表示位移场的空间x依赖性，级数的系数是未知时间t函数[7]。为了获得对滚珠丝杠轴的连续变形的有限元近似，应用Ritz级数展开的方法[6]，表达式为：

(6)

式中，ψu(x)∈RNu为基函数；qu∈RNu为广义坐标。

Ritz级数法中基函数必须满足要求: ① 线性无关，②位移必须是x的连续函数，③ 基函数必须满足全部几何边界条件[10]。满足这些条件才能保证收敛性。Nu是有限的，随着基函数的Nu的数量增加精确度得到提高[9]。

同理，滚珠丝杠的旋转扭转可以用有限级数近似展开：

(7)

式中，基函数ψθ(x)∈RNθ；广义坐标qθ∈RNθ。

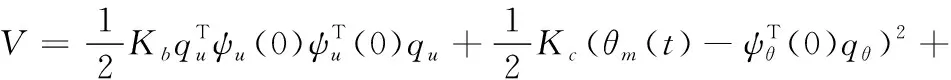
(8)

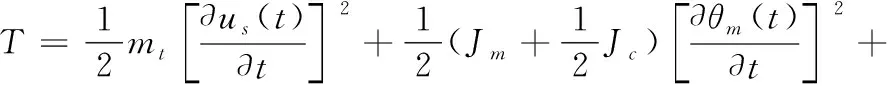
(9)

对于基函数中的ψu和ψθ有多种选择，常见的选择有递增频率的正弦函数和递增阶数的多项式函数。对于滚珠丝杠选择较低阶近似逼近，前两阶的可以通过Nu=Nθ=2近似得到。考虑滚珠丝杠传动的已知结构，仅将滚珠丝杠的第一部分作为柔性，忽略滚珠丝杠的无负载端部的变形。基函数为：

ψu,1(x)=1,x∈[0,L]

(10)

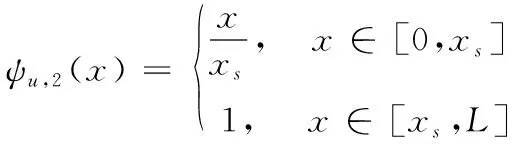
(11)

ψθ,1(x)=1,x∈[0,L]

(12)

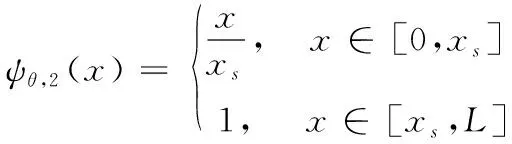
(13)

3 运动方程

定义系统的广义坐标q和广义力f，用矩阵的形式表达系统的动能和势能，并写出系统的质量矩阵和刚度矩阵，将动能和势能写成矩阵的表达形式。如下：

(14)

(15)

式中，Tm为丝杠电机的输入转矩；Tnm为螺母电机的输入转矩；

(16)

(17)

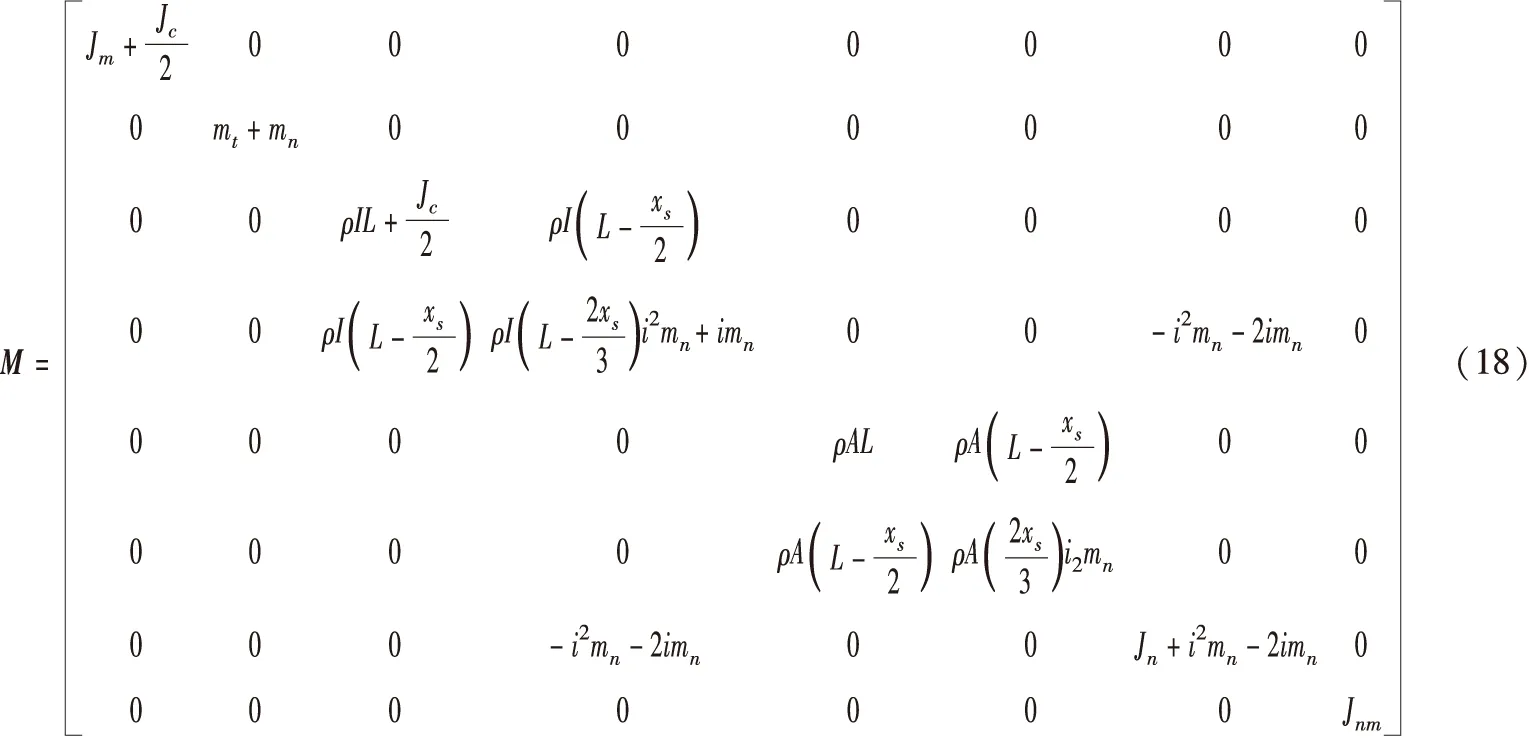
(19)

根据拉格朗日函数的定义，取L=T-V,并有如下形式：

(20)

将拉格朗日方程写成矩阵形式，得到系统的运动方程：

(21)

式中，M为质量矩阵；K为刚度矩阵。

4 谐振分析

根据已经求得的质量矩阵和刚度矩阵，考虑到结构的阻尼对模态的频率和振型影响很小，所以可将阻尼忽略。运用Matlab对动力学进行结构的频率响应仿真计算。

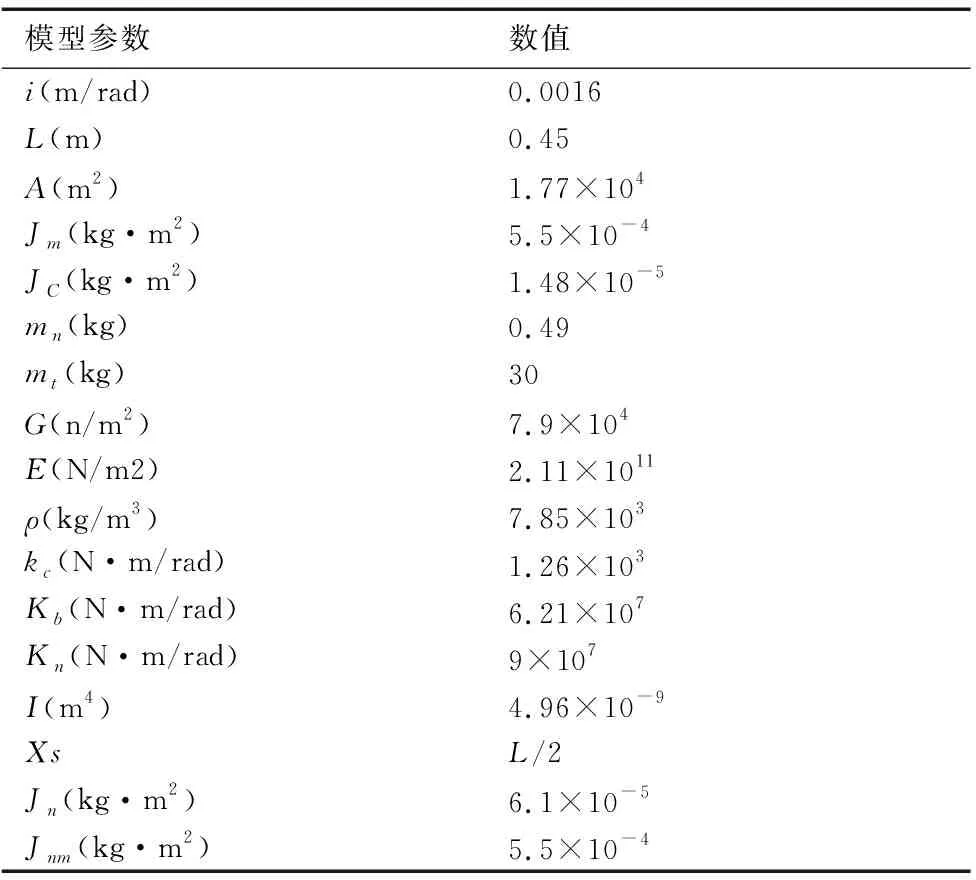
表1 双驱动系统的模型参数

考虑到双驱动传动系统中丝杠和螺母的转速一般不是很高，因此分析过程中不考虑滚珠离心力和陀螺力矩的影响[11]。根据表中的参数，求得前三阶固有频率依次为：f1=160Hz、f2=579.8Hz、f3=1872Hz。如图3为双驱动系统加速度频响特性曲线，滚珠丝杠传动系统当工作台位于丝杠的中间位置为振动的最薄弱环节。由图可知各部件的轴向振动的合成ω=160Hz时，系统会出现共振现象。

图3 丝杠处于中间位置时的频响特性

5 结论

本文针对双驱动伺服微位移进给系统进行研究得到如下结论：①将丝杆处理成铁木辛柯梁，使用Ritz级数进行处理，克服了集中参数法的不足。②利用建立系统的数学模型对系统进行MATLAB仿真分析比有限元法简单方便。③Ritz级数建模的方法可以得到简单的数学模型，有利于设计双驱动系统的控制算法，并为控制系统的高频抑制的研究提供了理论依据。