基于车辆健康状态评估的自适应分簇算法

叶 蕾，陈冬梅，曾令秋，韩庆文，王瑞梅

1.重庆大学 通信工程学院，重庆 400044

2.汽车零部件先进制造技术教育部重点实验室（重庆理工大学），重庆 400054

3.重庆大学 计算机学院，重庆 400044

1 引言

道路安全预警能够提醒道路车辆合理避险，从而提升道路交通安全水平，道路车辆可通过安全预警信息SWM交互获取周边车辆信息，并根据该信息合理制定驾驶策略，以避免潜在威胁转换为交通事故。

道路潜在威胁一般来源于健康状态不良车辆，如因驾驶员驾驶行为不良或车辆状态不良导致的行驶状态异常车辆，这类车辆自身或许并不会发生交通事故，但可能导致周边车辆发生事故，如车速缓慢，异常变道可能导致路怒症，诱发交通事故[1]。

车间通信是提高道路安全的重要技术，道路车辆通过交换异常车辆产生的SWM来避免潜在危险，区域内大量异常车辆产生的SWM将造成局部信息风暴，严重影响车间通信性能。车间安全信息的交换遵循3R原则，即在正确的时间向正确的车辆发送正确的信息。由于异常车辆的影响区域有限，因此异常车辆仅需要给影响范围内有通信需求的车辆发送SWM。面向SWM的分簇算法根据车间通信需求确定SWM交互区域，能够有效降低信息拥堵率，提高信息传输效率。分簇算法应重点考虑簇稳定性和信息传输效率两个因素。

簇头的选择机制会对簇稳定性产生重要影响。文献[2]提出的基于车辆运动性的簇头选择机制能够有效提高簇稳定性。文献[3]提出的动态簇头选择算法能适应驾驶者的行为，并且通过学习机制预测所有簇成员将来的速度和位置。结合地理位置和运动轨迹，文献[4]提出的车辆分簇算法能够提升车间通信性能。SWM与车辆的健康属性密切相关，在早期研究中，已经提出针对以事故车辆为中心的道路异常区域的分析和评估方法[5]，并且建立了基于车辆健康状况的原始簇结构[6]。文献[7-11]对此也有相关研究，在此不再赘述。这些研究表明车辆的健康属性会直接影响周围车辆的健康状况和危险等级，因此应根据车辆的健康状况和相应位置关系来构建SWM的传输簇。车辆的健康状况越差，产生的SWM越多，因此相较于低风险车辆，高风险车辆具有更大的通信需求，那么选择高通信需求的车辆作为簇中心将有助于维持簇的拓扑结构。

基于频率资源有限和802.11p协议中传统的信道竞争接入机制两个因素，如果簇内过多车辆有SWM交换需求，则会造成较长的信息交换时延和较低的信息传输效率。文献[12]提出车辆互连度量和聚类协议，以提高车辆连通性，文献[13]提出的总体本地流动性标准一定程度上提高了信息传输效率。簇内SWM的传输效率与簇中高危车辆的数量和簇的范围有密切关系。Lan Kun-Chen等人相信车辆簇的范围应该随着区域内车辆数目的变化而变化[14]，并且应该采用现实车辆跟踪数据来说明车辆簇的形成与相应参数之间的关系，例如路线选择，交通信号灯和路边节点的位置。本文认为簇的范围与簇内SWM通信需求的数量有关，因此根据簇内通信需求数量自适应调整簇的范围能够降低车辆争夺传输资源的可能性，从而大大提高SWM的传输效率。

因此，本文将重点从车辆健康状况，车间通信需求和簇范围三个方面展开研究，主要内容如下。

（1）基于车辆的固有属性和实时属性，提出车辆长期和短期健康状况评估方法，判断车辆的危险等级。

（2）提出基于车辆健康状况的自适应分簇算法，从信息源方面降低网络开销，提高簇稳定性。

（3）提出基于簇内通信需求数量的簇范围自适应调整机制，从信息传输范围方面进一步降低信息拥堵，提高传输效率。最后详细介绍了簇的形成和维持过程。

2 车辆健康状况评估

车辆健康状况的评估结果是基于车辆健康状况的分簇算法的首要指标。根据以前的研究结果，选择驾驶员驾驶行为和车辆状态作为决定车辆健康状况的两个主要因素，并且这两个因素都应该通过实时属性和固有属性来说明。道路车辆间通过交互包含车辆健康状况的SWM信息来合理规避道路中潜在的危险车辆，因此将个人车辆（PV）定义为包括驾驶员在内的道路上未发生事故的车辆，PV的特性应包括实时属性和固有属性。用长期健康参数（L HV）和短期健康参数（SHV）来综合评估车辆健康状况。

车辆PVj的长期健康参数主要由固有属性决定，主要参数包括：

其中Vtype为车辆类型，kTV为车辆已行驶公里数，ACEdriver为驾驶员累计驾驶经验，WLi为权重因子。

众所周知，车辆行驶的时间越长越危险，因此车辆健康状况与kTV呈线性关系，文献[15]提出车辆事故率与车辆类型的关系，在所有的道路事故中，小型车的死亡率最大，其次为大型卡车。Vtype和kTV的值可以通过控制中心得到，具体定义见表1。

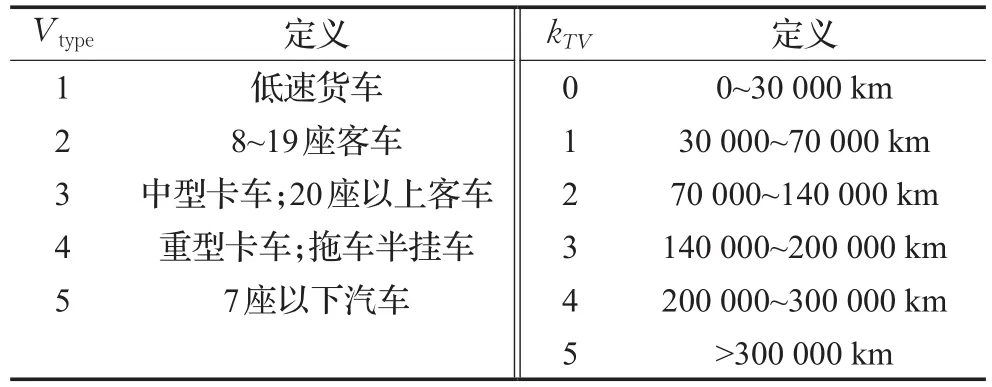
表1 V type与kTV数值表

ACEdriver由驾驶经验因素ACEdriver1和车辆熟悉因素ACEdriver2共同决定。

低龄驾驶人由于驾驶经验缺乏，实际道路驾驶技能生疏，复杂路况下抗干扰能力相对较差、应急反应处理能力不足，容易造成周边车辆不安[1]，其危险性最大。同时图1显示的2015年上海各个驾龄的事故率也可说明低领驾驶人的危险性最大，根据分析可定义ACEdriver1的值，具体数值见表2。

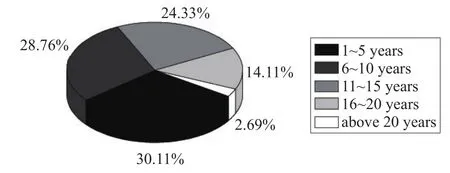
图1 2015年各驾龄事故率

表2 ACE driver1数值表

ACEdriver2与驾驶员使用对象车辆的次数有关，可以通过以下公式计算：

车辆PVj的短期健康参数主要由实时属性决定，主要参数包括：

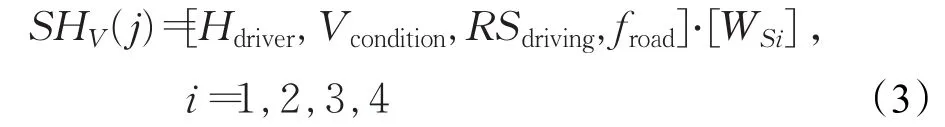
其中，Vcondition为车辆的实时状态，可通过车载传感器模块获得，Hdriver为驾驶员健康状况，可通过穿戴设备来实时监测[16]，RSdriving为实时驾驶状态，可通过汽车行驶状态实时记录装置获得[17]，具体定义和解释如表3所示。

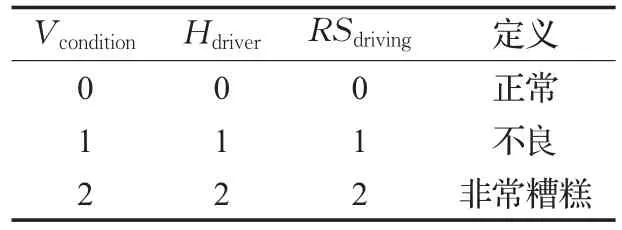
表3 实时参数数值表

综合考虑车辆的长期健康参数LHV和短期健康参数SHV可以得到车辆健康值的计算公式：

其中β1和β2分别为LHV和SHV的权重因子，由于LHV对车辆的健康状况起主导作用，因此定义β1＞β2。

例如一辆行驶了8万公里的低速客车，一位驾龄为2年的驾驶员首次接触该车辆，若权重因子WLi=[0.8 0.1 0.1]，则该车的长期健康参数为LHV=[1 2 4+e1-1]⋅[0.8 0.1 0.1]T=1.5，假设通过车辆传感器与驾驶员佩戴的健康状况检测器得知目前该驾驶员的身体状态与驾驶状态均正常，但是车辆实时车况不良，若权重因子WSi=[0.3 0.5 0.2]，由于车辆均处于同一路段，因此道路因素可以不予考虑，则该车的短期健康参数为SHV=[0 1 0]⋅[0.3 0.5 0.2]T=0.5 。

根据车辆的健康值，可以将车辆分为健康车辆（HV）和亚健康车辆（SHV），其中亚健康车辆又根据不同情况进一步分为长期亚健康车辆（LSHV）和短期亚健康车辆（SSHV），通过设置长期阈值（L Hth）和短期阈值（SHth）对SHV进行分类，具体分类规则如下：

（1）如果 LHV(i)≥LHth，则 PV(i)为LSHV。

（2）如果 LHV(i)＜LHth，且 SHV(i)≥SHth，则 PV(i)为SSHV。

（3）如果 LHV(i)＜LHth，且 SHV(i)＜SHth，则 PV(i)为HV。

3 基于车辆健康状况的自适应分簇算法

为提高SWM传输性能，本章提出基于车辆健康状况的自适应分簇算法。簇为一个圆形区域，其中心具有簇头（CH），簇将随着CH一起移动。为确保高危信息的传输质量，算法重点解决三个关键问题，包括CH的选取和转移，簇范围的自适应调整，簇的动态行为。

3.1 CH的选取和转移规则

簇头的稳定性影响簇的稳定性。对于以传输SWM为目的的簇，选择一个具有稳定传输需求的车辆作为簇头将有助于维持簇的稳定性。由于PV间的传输需求与车辆的健康状况密切相关，因此PV的健康值将作为CH选取和转移过程中的主要依据。

3.1.1 CH的选取

当健康的车辆转变为SHV时，如果其周围没有现存的簇，则会产生一个新簇。由于SHV由实时属性决定并且会随着时间变化，因此为了确保簇的稳定性，在簇头的选取过程中应首先考虑LHV。具体选取规则如下：

（1）如果区域内存在多辆LSHV，则选取LSHV中LHV最大的车辆作为簇头。

（2）如果区域内没有LSHV，但是存在多辆SSHV，则选取SSHV中HV最大的车辆作为簇头。

（3）如果区域内既没有LSHV，也没有SSHV，则该区域不需要构建簇。

3.1.2 CH的转移

当有新的SHV驶入现存簇内，或当簇内车辆的健康属性发生改变时，CH可能会发生转移。如果簇内一旦出现LHV或SHV更高的SHV时，CH就发生转移，那么CH的频繁转移将降低簇的稳定性。为确保簇头选取的权威性和稳定性，提出迟滞CH转移规则。

假设车辆 j的健康值高于现有簇头i，定义健康值的百分比差为：

设定百分比差阈值PDth来决定CH是否转移。假设原始簇头为PV(i)，竞争簇头的车辆为PV(j)，CH的转移规则如下：

（1）如果 PV(i)和 PV(j)均为LSHV，当 PDij＞PDth时，CH发生转移。

（2）如果 PV(i)和 PV(j)均为SSHV，当 PDij＞PDth时，CH发生转移。

（3）如果 PV(i)为SSHV，PV(j)为LSHV，则CH直接转移。

（4）如果 PV(i)为LSHV，PV(j)为SSHV，则保持原簇头。

3.2 簇范围自适应调整机制

区域内所有的SHV都将产生SWM，并尝试将其传输给邻居车辆，因此区域内即时信息量的大小难以估计，如果等待传输的信息累计到一定数量，将会发生局部信息风暴。所以应该控制簇内信息数量来避免局部信息量过大造成的通信效率下降。对于车辆簇来说，最直接的方式即根据簇内通信需求的数量自适应调整簇的范围。

定义信息发送车辆i和接收车辆 j之间的通信需求关系Demand(i,j)：

其中dij为车辆i和 j之间的距离，ρ为区域车辆密度，α1和α2分别为发送车辆和接收车辆的权重因子，由于发送车辆的健康状况对于通信需求有更重要的影响，所以设置α1＞α2。

根据预先设定的通信需求关系阈值Demandth对通信需求进行进一步过滤，如果Demand(i,j)＜Demandth，则车辆i和 j之间无SWM传输需求，如果Demand(i,j)≥Demandth，则车辆i和 j之间具有有效通信需求，并且Demand(i,j)的值越大，SWM的传输优先级越高。

假设簇内有n辆车，那么可以得到n×(n-1)个通信需求值，并且可以根据Demandth，得到有效通信需求的个数NVCD。簇半径为CH到簇成员的最大距离，其应该根据簇内NVCD的变化进行自适应调整，从而避免信息风暴。

然而簇半径的频繁改变将会增加开销并且大大降低信息传输效率，所以将簇半径分为四个等级，并且所有簇的初始半径均为最大等级。将簇内能够承担的最大通信需求数定义为Nth，并以此为标准调整簇半径，具体规则如下：

（1）如果NVCD＞Nth，则降低半径等级，缩小簇范围以减少簇内通信需求数。

（2）如果NVCD≤Nth，则保持簇半径不改变。

3.3 簇的动态行为

簇形成之后会随着CH移动，当簇内车辆的位置发生改变时，簇将会分离或者合并。簇的主要动态行为如下。

3.3.1 簇的分离

当PV离开原有簇的区域，并且未进入其他簇的区域时，即PV无法检测到原有CH和任何新的CH，则可能会发生簇的分离，形成新的簇。新簇的CH依然通过上述CH选取规则来选取。这个过程称为簇的分离，一个簇分离为两个簇。

3.3.2 簇成员改变

当PV离开原有簇的区域，进入到其他簇的区域时，即PV检测到新的CH而非原有的CH，PV将加入新的簇作为簇成员或者根据CH转移规则成为CH。

3.3.3 簇的合并

当两个CH进入彼此所在簇的覆盖区域时，簇将发生合并。新簇的CH将根据CH选取原则进行选取，此时两个簇合并为一个簇。

4 簇的生成和维持过程

假设所有的PV都可以根据GPS和车内的传感器得到自身的位置信息和健康属性。根据上述章节中提出的自适应分簇算法和相关规则，设计簇的产生和维持过程。

4.1 簇的生成

当PV进入道路环境，或离开原有的簇结构时，他们将进入默认信道进行簇的生成。PV根据LHV和SHV得到自身健康状态，如果为SHV，则广播自身的状态信息（AM），包括位置信息和健康属性，区域内所有的PV都将收到邻居SHV的AM，然后与自身健康状态进行比较，根据上述CH选取规则选取CH。CH计算簇内通信需求数量，并以此确定簇半径，然后向所有的簇成员广播确认信息（BM），收到BM的PV将加入该簇成为簇成员，在预设时间内未收到BM的PV将进入下一个簇生成过程。

4.2 簇的维持

簇生成之后将进入簇的维持过程。在这个阶段，CH定期广播BM。收到BM的簇成员将继续留在簇中，并向CH发送AM更新位置信息和健康属性，CH根据收到的AM更新簇成员属性并根据需求调整簇半径。而在预设时间内未收到BM的簇成员则返回到簇的生成过程。如果CH收到另一个CH的BM，两个簇将会合并为一个簇。

完整的分簇过程如下。

准备：所有VENET中的车辆均切换到默认信道

步骤1簇的产生

1.1 PV根据健康因素确认自身是否是SHV

如果PV是SHV，则广播AM

1.2 PV收到邻居车辆的位置信息和健康属性

1.3 根据CH选取规则，如果PV是CH

根据有效通信需求数Nvcd确定簇半径

向簇成员广播BM

1.4 根据CH选取规则，如果PV不是CH

如果收到CH发送的BM，则加入簇

如果没有收到BM，返回1.1

步骤2簇的维持

2.1 CH定期广播BM

2.2 如果簇成员收到CH发送的BM

继续留在簇中

通过AM向CH更新位置信息和健康属性

2.3 如果簇成员没有收到CH发送的BM

在预设时间内继续等待BM

如果收到BM，则重新加入簇或者加入一个新簇

如果没有收到BM，则回到簇生成过程

2.4 CH更新簇成员属性

如果需要，根据CH转移规则进行CH转移

如果需要，根据簇内有效通信需求数调整簇半径

2.5 如果CH收到其他CH的BM

CH竞争并进行簇合并

5 仿真结果与分析

本文运用基于智能体的建模仿真平台Anylogic[18]来进行分簇过程的仿真分析。Anylogic 6.0平台结合基于智能体的仿真模型搭建框架结构，用于模拟复杂的车辆道路环境。

5.1 模型假设

（1）道路车辆：道路车辆通过对SWM的交互来获取周边行驶状态异常（驾驶行为不良或车况不良）的车辆信息，以避免潜在威胁，因此模型中的道路车辆定义为道路中包括驾驶员在内的未发生事故的车辆。

（2）车辆健康参数：模型的重点在于验证基于车辆健康值的分簇算法的有效性与稳定性，因此车辆健康参数的采集与计算不在该模型考虑范围内。由于道路车辆的健康值总是大于0，且在实际情况中，车辆状态极佳与极差的均为少数，大部分车辆处于中间健康状态，因此为了研究方便本文定义车辆的长期健康参数与短期健康参数均服从正态分布。模型中车辆的LHv与SHv分别为正态分布中的随机数。

5.2 模型设置

本文构建的模型中包含三个智能体，包括控制车辆运动流程的主智能体，定义车辆属性的车辆智能体和计算簇相关数据的簇智能体。模型的时序流程如图2所示。

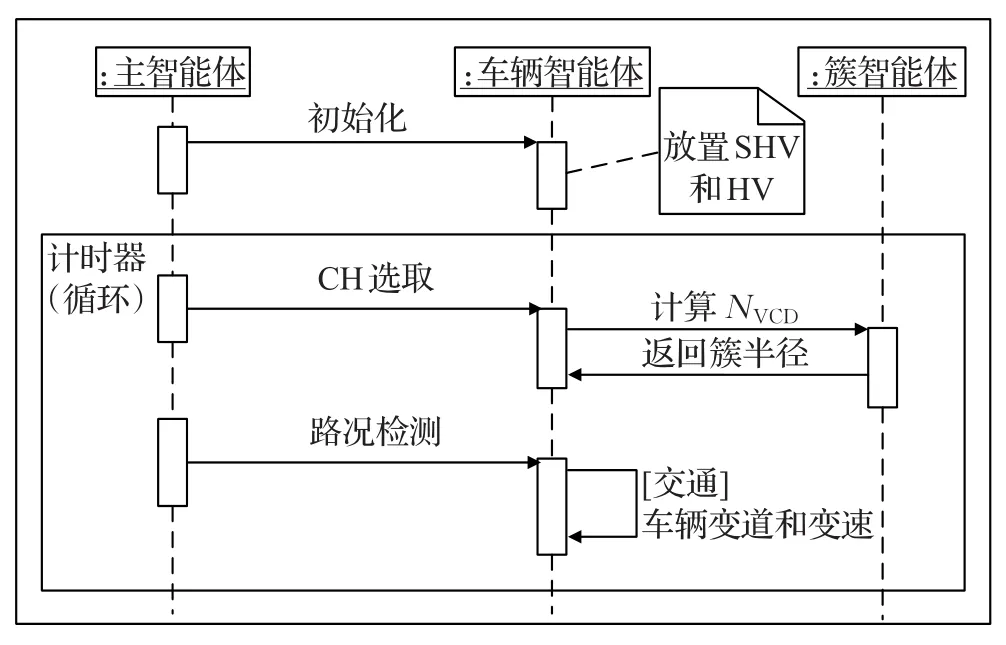
图2 模型时序图

在建模过程中，首先在主智能体中进行模型初始化。初始化包括两个部分，一是初始化道路车辆的位置和速度，另一个为初始化所有车辆的LHv与SHv。主智能体中的定时器将定期触发车辆智能体中函数，当函数被触发时，车辆智能体将遍历所有的车辆计算出每辆车的Hv并通过CH选取规则确定CH并随后计算簇的半径。车辆的变道和变速等运动行为也由车辆智能体控制实现。

5.2.1 簇的动态行为仿真

模型初始设置如下：

（1）道路设置为390 m的单向3车道。

（2）道路车辆的速度范围为30～60 km/h。

（3）分簇过程将遵循第3、4章中提出的算法。

（4）其他参数如表4所示。

表4 模型参数值

仿真结果如图3，图4所示，展示了簇的生成和维持过程，包括CH的选取、转移，簇半径的改变和簇的动态行为。

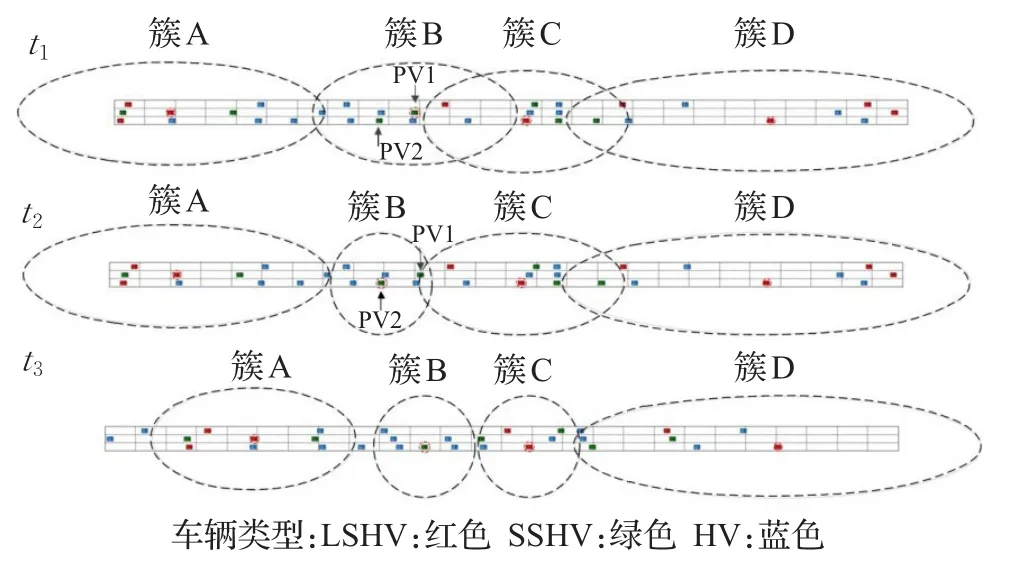
图3 簇的生成过程图

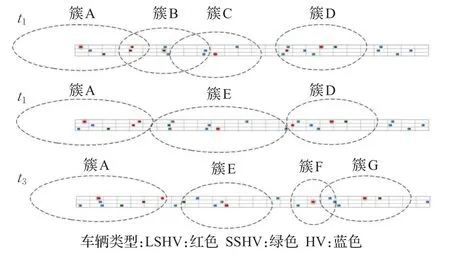
图4 簇的动态行为过程图

在图3中，t1时刻，根据CH选取规则和簇半径判定原则，道路中生成了4个簇。可以看出LSHV首先被选取为簇头，当道路中没有LSHV时，选取了HV最大的SSHV作为簇B的簇头，并且根据各个簇内NVCD与Nth的比较，确定了簇A、B、C、D的半径分别为75 m，50 m，50 m和100 m。

t2时刻，由于车辆SHV的改变，按照CH转移规则，簇B的簇头由PV1转变为PV2，同时随着簇头的转移，簇内NVCD也发生改变，因此簇半径随之改变。

t3时刻，由于簇内车辆的移动，簇内NVCD发生改变，因此簇C的半径由50 m减小为25 m。

在图4中，t1时刻，簇B的CH向簇C靠近，因此在t2时刻，簇B和簇C合并为簇E，新的CH同样根据CH选取规则选取。同时随着车辆的移动，t2时刻的簇D在t3时刻分离为簇F和簇G。

模型仿真参数的统计输出结果如图5所示。仿真跟踪了通信需求数和簇半径的变化关系。结果表明簇半径与需求密度成反比，其中通信需求密度为NVCD与簇面积的比值。

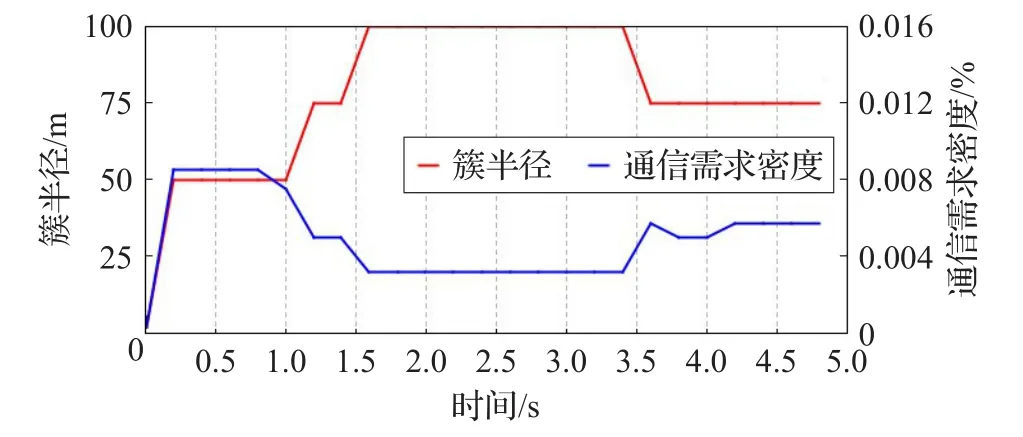
图5 簇半径与通信需求密度关系图

5.2.2 分簇算法性能检测

本文与文献[19]中的三种成簇算法进行成簇稳定性的对比。

模型设置：

（1）道路设置为2 000 m的单向3车道。

（2）道路车辆的速度范围为36～108 km/h。

（3）分簇过程将遵循第3、4章中提出的算法。

（4）其他阈值参数如表4所示。

为说明分簇算法的稳定性，定义稳定因子的计算方法如下：

即CH持续时间与仿真时间的比值，统计计算不同车辆数下稳定因子的值，由于文献[19]仅统计了CH持续时间，为方便直观比较算法性能，结合算法的仿真时间将文献[19]中的结果换算为稳定因子，得到结果如图6所示。

图6 稳定因子随车辆数变化图

从图中看出算法min-id的簇稳定性在各种车辆数下均表现较差，算法SD与max-degree的簇稳定性随车辆数波动较大，而本文算法能够在不同车辆数下，均保持较高的簇稳定性。综上，本文算法具有良好的簇稳定性和优秀的自适应能力。

6 结束语

道路车辆簇的稳定性和有效性直接影响V2V信息交换的性能，因此在分簇算法的设计中应予以重点考虑。

基于车辆健康状况的自适应分簇算法能够有效减少局部信息风暴，提高SWM传输效率。根据车辆健康评估方法将车辆分为健康和亚健康两种状态，只有亚健康状态的车辆才传送SWM，从信息源方面减少了区域信息量。在CH选取过程中采用LSHV优先准则和迟滞CH转移规则来确保簇的稳定性。通过计算簇内通信需求数实现簇范围的自适应调整，从信息传输范围方面减少了区域信息量。基于Anylogic 6.0平台的仿真结果说明了该算法的三个优点。第一，合理降低CH转移概率；第二，簇范围能根据簇内通信需求数进行自适应调整；第三，在不同车辆密度下，车辆簇都具有良好的稳定性。这些均能说明该算法的有效性。

在未来的研究工作中，将运用实际道路对算法进行测试。相信本文将有助于推广V2V SWM传输机制的应用。