一种基于NSST的图像去噪算法

陆 焱，胡玉荣

（荆楚理工学院 a.计算机工程学院；b.科技处，湖北 荆门 448000）

0 引言

由于环境和设备的原因，通常采集到的图像会含有噪声。而噪声对图像的检测有着非常大的影响，较好的图像去噪能力是检验一个图像处理系统是否优秀的重要标准，若噪声处理不好，将会出现漏检甚至根本检测不到图像细节的现象。因而，多年来人们对噪声反复进行了研究，产生了许多经典的算法［1］，利用小波变换的多分辨率分析可以有效去除噪声，并且很好地保留图像细节［2-6］。虽然基于小波的经典去噪算法［7］在噪声标准差较小的情况下可以实现去噪，但当噪声标准差较大时去噪效果有待提升。因此，出现了基于小波变换的阈值收缩和比例收缩算法［8］。小波阈值去噪是最常用的一种去噪方法［9］，该算法在噪声较小的情况下可以取得较好的效果，但在噪声比较大时，效果仍然不理想［10］。目前，基于阈值萎缩的小波去噪方法的研究仍然非常活跃，研究集中在如何最大限度地获得信号的先验信息，确定更合适的阈值，达到更高的去噪效率。

小波阈值图像去噪方法［11］因为实现较简单、计算量较小而被广泛应用。但是小波分析在一维时所具有的优点并不能推广到二维乃至更高维，即不能从刻画点奇异推广到刻画线奇异乃至面奇异。并且对于图像来说，边缘不连续性是按照空间分布的，这种奇异性影响了小波展开级数中的许多项，因此，小波变换在去噪上展现出了许多不足。为此，研究人员提出了多尺度变换工具［12］，在众多多尺度变换工具中，非下采样Shearlet变换（non-subsampled Shearlet transform，NSST）具有分解速度快、方向敏感的优点，且没有下采样的过程，使其具有平移不变性。其分解系数与小波分解系数相比能够较准确地表示图像内容细节信息，有利于提升去噪效果。因此，本文选用NSST分解含噪图像，分解后的图像包含低频子带和高频子带系数，图像的绝大多数信息包含在低频子带中，高频子带中包含轮廓、曲线等细节信息和噪声，通过阈值去噪算法处理高频子带，去除噪声，由处理后的子带结合低频子带通过NSST逆变换重构得到去噪后的图像。

1 非下采样Shearlet变换

1.1 Shearlet变换

Shearlet变换［13-14］具有分解速度快、方向敏感性和平移不变性的优点。本文利用该变换分解含噪图像，由于本文灰度图像为二维图像，即维数为n=2时，在合成小波理论的基础上，通过仿射系统把几何和多尺度结合起来构造Shearlet波。具有合成膨胀的仿射系统定义为

其中ψ∈L2(R2)，A表示各向异性膨胀2×2的可逆矩阵，该矩阵控制Shearlet变换的尺度，Aj与尺度变换相关联。S是2×2的剪切矩阵，该矩阵为可逆矩阵，|detS|=1，Sj与保持面积不变的几何变换相关联。如果MAB(ψ)具有如下形式的紧框架条件，则MAB(ψ)的元素称为合成小波，即对∀f∈L2(R2)，有

对于任意的尺度参数α>0和方向参数s∈R，α和s取不同值时，Shearlet变换的频域支集如图1所示，本文与文献［15］中选用同样的参数α=2，s=1。矩阵A、S定义为

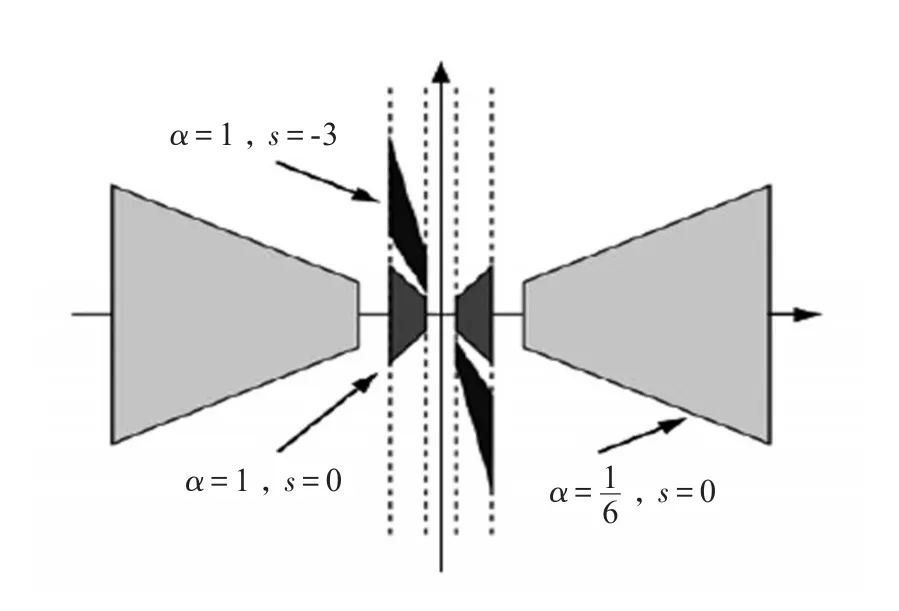
图1 不同α和s的Shearlet频域支集图Fig.1 Chart of Shearlet frequency domain support with differentαands

特别地，当α=4，s=1时，即，其形式就是Shearlet。

假设有下式：

且，对于∀j≥0都有

图2 每个Shearlet频域支撑大小Fig.2 Frequency domain size of each Shearlet

由图3可知，不同尺度的梯形支撑区域关于原点对称。该区域能够很好地表示图像曲线特征、边缘细节特征和奇异性特征，更加适合描述图像特征。

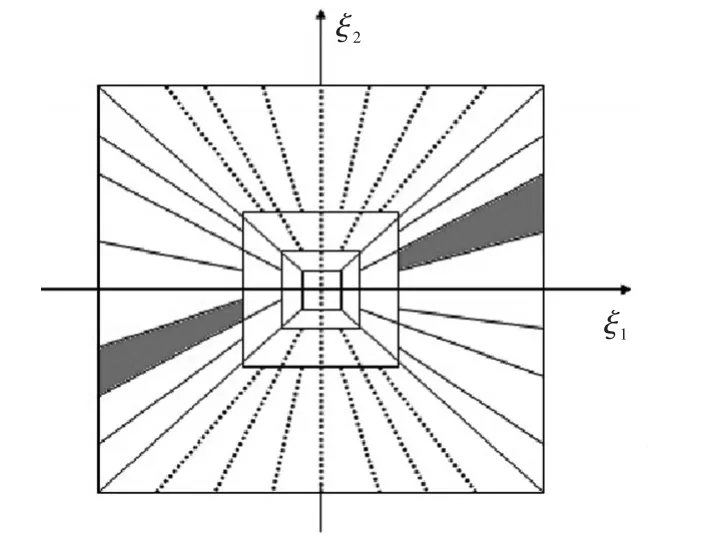
图3 Shearlet频域剖分图Fig.3Decomposition of Shearlet frequency domain

1.2 非下采样过程

Shearlet变换的下采样过程容易产生振铃现象，非下采样Shearlet变换通过级联非下采样金字塔滤波器和非下采样剪切波滤波器这两个下采样过程，与拉普拉斯金字塔相比，非下采样金字塔滤波器组没有下采样的过程，因此具备平移不变性。它能够将图像分解为与原图像相同大小的高频子带和低频子带，如图4所示，每层分解是在上一层的低频子带上进行分解，得到k+1条子带信息，有k条高频子带，1条低频子带。与Shearlet变换相比，这一特性避免了图像在奇异点处产生伪吉布斯现象。非下采样剪切波滤波器将高频子带分解为方向子带，使得NSST具有方向敏感性。因此，NSST能够在尺度和方向方面很好地表示图像信息，本文利用NSST分解含噪的图像。

该平台面向用户界面统一采用直接经纬度坐标系统,所有非经纬度坐标的原始资料在服务器端转换成经纬度,由于目前气象要素显示精度要求不高(最大精度也就0.01度),各种大地坐标基准之间的差别可以忽略不计。

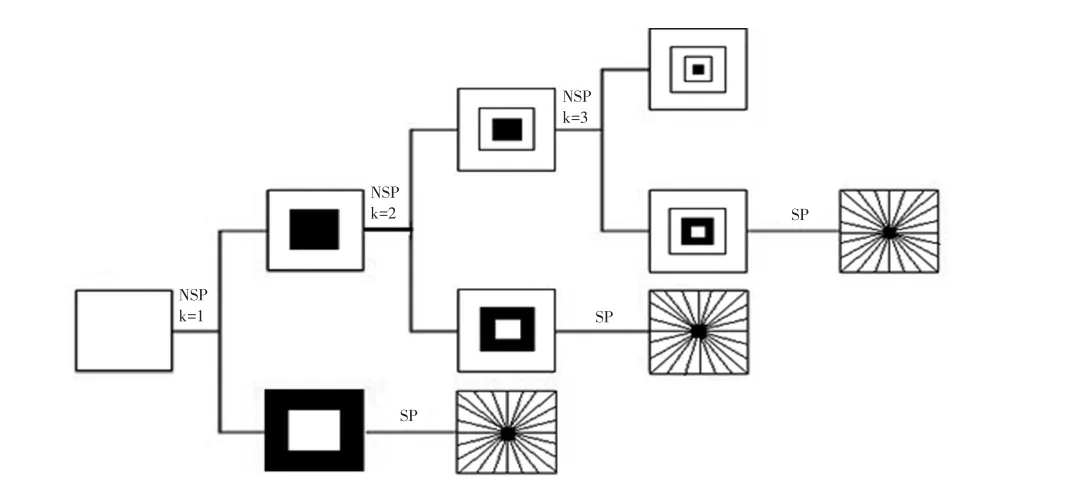
图4 NSST的多个尺度多个方向的分解子带Fig.4 Subband decomposition of NSST with multiple direction and multiple scale

2 图像阈值去噪算法

2.1 图像阈值去噪算法

使用NSST对图像进行多尺度分解，由Nastar等［16］的统计可知，低频子带中包含图像的绝大多数信息，噪声及图像的边缘信息主要集中在分解图像的高频子带中。因此，图像去噪需对高频子带分解系数进行处理。

由图4可以看出，NSST第k条低频子带分解得到第k+1条高频子带和低频子带，NSST分解的图像在各个尺度上包含丰富的方向信息，根据胡海智等［17］对图像去噪进行的研究，在NSST分解过程中，图像边缘细节信号的分解系数沿着尺度分解传递，有较大的传承，即各个尺度上，同方向、同位置的分解系数具有相关性，而噪声对应的系数在传递过程中衰减很快，各个尺度上同方向、同位置的分解系数相关性不明显。因此，可以利用相邻尺度各方向子带系数间的差值来区分噪声和图像信号，由第k个尺度和第k+1个尺度相邻方向系数的差值大小，来判别第k+1个尺度中图像边缘系数和噪声系数。

如果图像边缘的方向在高频子带的两个方向之间，则两者的差同样很小，所以上述条件不足以完全判断出噪声与图像边缘系数。但由于在NSST的系数分解中，图像边缘细节等分解系数沿尺度传递，不同尺度间的系数具有传承性，所以不同尺度中相同位置、相同方向的系数具有相关性。通过尺度间系数传承性判别作为另一判别条件。

为得到方向信息，设尺度相关系数CorS为

其中S表示尺度数，N表示方向数，16；N=1,2,…,32，设方向相关系数CorD为

其中S=3，N=1,2,…,32。

由于边缘具有方向信息，由同一父方向系数分解得到的相邻子方向系数具有相关性，而噪声系数则无此关系，因此，使用尺度相关性系数进行判定。相同父方向系数的相邻子方向系数之间差值较大者为方向系数，否则为噪声系数

其中S=3，N=1,2,…,16，T1为阈值系数。

其中S=3，N=1,2,…,32，T2为调节系数。

因此，本文对高频子带系数进行处理，首先利用（10）式判断信号是否为图像边缘信号，若不是，则继续使用（11）式判断，若是图像边缘信号，则判定为第k+1尺度的图像边缘信号，若是噪声，则置零。同时，由于第k尺度的一个方向系数分解为第k+1尺度的方向系数，若根据前一步判断出第k+1尺度的方向系数均为边缘信号，则对应的第k尺度系数判别为图像边缘信号，否则判别为噪声，进行置零。

为了有效确定阈值调节系数T1、T2的取值，本文根据阈值与去噪图像的峰值信噪比（peak signal to noise ratio，PSNR）的关系确定阈值取值［18］。

对由（10）式和（11）式求取差值和相除后的值进行排序，设阈值位置比例为R，用于确定阈值的位置，取去噪图像的PSNR为最大值时R值为阈值最佳位置比例值，用以确定阈值的取值。

例如，设阈值位置比例为R，本文选取添加噪声为30的Lena图像，R以0.01为步调，在0.01到1之间进行取值，可以得到去噪图像PSNR随R变化的曲线如图5所示。从图5可以看出，当R取值0.03时，去噪图像的PSNR最高为32.58 dB。

图5 Lena去噪图像PSNR随R变化的曲线Fig.5 Changes of Lena denoising imagePSNRwithR

2.2 图像阈值去噪算法流程图

本文图像阈值去噪算法流程图如图6所示，先对含噪图像作NSST分解，得到低频子带和高频子带；低频子带中包含图像的绝大部分信息，噪声信息主要集中在高频，去噪主要对高频子带信息进行处理；由公式（10）和（11）判断是否为图像的边缘细节信号，若是，则不做任何处理；若不是，则将子带系数置零；由处理后的高频子带和低频子带通过NSST逆变换，得到去噪后的图像。

图6 本文去噪算法流程图Fig.6 Flow chart of denoising algorithm in this paper

3 结果与分析

本文算法以及对比算法都在32位Windows10操作系统，硬件平台为Intel（R）Core（TM）处理器、2.00 GB内存、3 GHz主频的计算机上，以及实验软件平台为Matlab7.0.1，选取图像标准数据库中的Lena图像，图像来源为 http：//decsai.ugr.es/～Javier/de-noise/test-images。为了体现本文算法的有效性及可行性，选取添加高斯噪声标准差为30、50的Lena、Barbara图像进行实验（见图7），对比算法选用小波硬阈值去噪算法［19］、小波软阈值去噪算法［20］、图像去噪中比较经典的算法BM3D［21］以及基于NSST的正态逆高斯分布图像去噪算法（NSST+NIG）［15］，实验结果如图8～图11所示。

3.1 主观评价

本文以主观视觉效果作为主观评价指标，图7为Lena、Barbara原图像，图8～图11为实验后的结果，从图中可以看出，本文算法去噪结果优于对比算法，小波硬阈值、软阈值均可以实现去噪，但出现一定程度的平滑和去噪不彻底，如图9（b）小波硬阈值去噪后的图像，噪声去除不彻底，图9（c）小波软阈值去噪后的图像，帽子上的纹理信息、帽檐处羽毛等细节信息存在一定程度的平滑；BM3D算法是图像去噪中比较经典的算法，通常作为图像去噪算法的衡量标准，去噪后的效果明显优于小波硬阈值、小波软阈值去噪算法；基于NSST的正态逆高斯分布去噪算法利用了NSST能够从多个尺度多个方向上表示图像细节信息的优点，能够在去噪的同时更好地表示图像的细节纹理信息；本文算法在去噪时利用阈值去噪算法，有效确定阈值调节系数T1、T2的取值，由阈值与去噪图像的PSNR的关系确定阈值取值，使得去噪后的图像更具有鲁棒性。从图10和图11中Barbara图像去噪结果可以看出，本文算法在去噪的同时可以很好地保留图像的细节信息，如Barbara图像的裤管和桌布包含更多的纹理信息，去噪后的图像能够保留纹理细节信息。由图8和图9及图10和图11对比可以看出，对于含噪声标准差大的图像去噪优越性更加突出。

图7 Lena、Barbara原图像Fig.7 Original images of Lena and Barbara

图8 噪声标准差为30的Lena图像去噪结果Fig.8 Image denoising results of Lena with noise standard deviation as 30

图9 噪声标准差为50的Lena图像去噪结果Fig.9 Image denoising results of Lena with noise standard deviation as 50

图10 噪声标准差为30的Barbara图像去噪结果Fig.10 Image denoising results of Barbara with noise standard deviation as 30

图11 噪声标准差为50的Barbara图像去噪结果Fig.11 Image denoising results of Barbara with noise standard deviation as 50

3.2 客观评价

由表1可以看出，本文算法去噪后PSNR大于对比算法，小波硬阈值去噪后PSNR最小，去噪效果欠佳；小波软阈值去噪避免了直接选取阈值使得图像出现过度平滑，去噪后PSNR高于硬阈值去噪算法；BM3D去噪算法为经典的图像去噪算法，去噪后的峰值信噪比优于小波阈值去噪算法；NSST+NIG算法利用了NSST能够更加准确地表示图像的细节信息，使得去噪后的PSNR有所提升；本文去噪算法既利用了NSST的优势，又结合了由去噪图像的PSNR与阈值的关系确定阈值，使得阈值的选取更加灵活，去噪效果进一步提升。

表1 本文算法及对比算法去噪PSNR结果（Lena图像）Tab.1 PSNRresults of the proposed algorithm and contrast algorithm（Lena image） /dB

4 结论

图像去噪是图像检测与识别的关键，本文选取NSST作为多尺度分解工具能够更好地描述图像细节信息，利用阈值去噪方法对高频子带分解系数进行处理，最后由高、低频子带分解系数重构原图像，从而得到去噪后的图像。仿真实验结果表明，NSST对尺度分解工具比小波变换能最优表示二维图像的奇异曲线，本文阈值由系数和PSNR共同确定，增强了图像去噪的鲁棒性，在视觉效果和峰值性噪比方面均有所提高，证实了本文算法的有效性。