美国AC版初中数学教材编排特点及启示
——以“研究整数”一章为例
范连众,孔凡哲
(1.东北师范大学教育学部;2.辽宁省大连市甘井子区教师进修学校)
尽管我国学者在研究美国教材方面的成果比较丰富,但由于教育体制、传统、研究特长等各方面的差异,在具体章节层面进行微观研究的还很少.
本研究以美国McGraw-Hill公司2008年出版的《Mathematics:Applications and Connections》(以下统称“AC版教材”)中的“研究整数”一章为研究对象,就其编写特点进行详细剖析,希望能为我国教材的编写修订提供参考借鉴.
一、教材的整体编排结构
AC版教材共有三册,供6~8年级的学生使用.第一册共分十三章,以代数领域的内容居多,但在每一章中,也会有与几何和统计相联系的内容.“研究整数”是在第一册中的第十一章,主要内容属于代数领域,还涉及到几何变换领域的内容.例如,在坐标系中用有序数对表示点的位置,图形的平移与轴对称变换.
为了更清楚地了解第一册教材的编排特点,现将各章的名称和主要学习内容罗列如表1所示.
第十一章“研究整数”共有十一个小节,每一小节都从实际问题入手,具体名称和学习内容如表2所示.由表2可以清楚地看到在代数知识学习的过程中,几何知识与问题解决的策略性知识,都有效地整合在一起.

表1:AC版教材整体编排结构
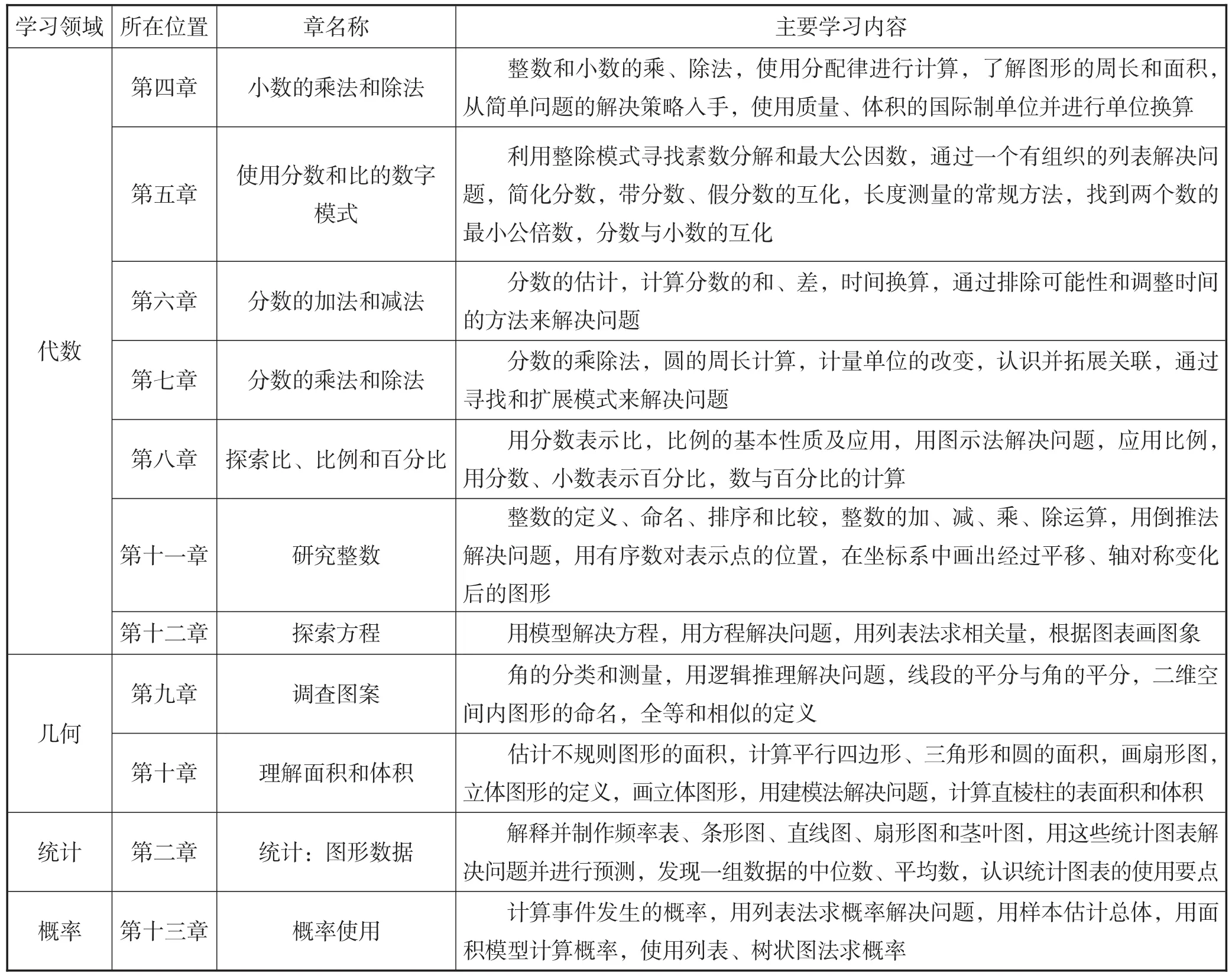
续表

表2:第十一章各小节的内容编排
二、教材的具体结构分析
1.首当其冲的章项目
在学习一章知识之前,教材首先给出章项目(Chapter Project),一般占据2页篇幅,第1页是为章项目配备的主题彩图,以及本章将要学习的主要知识点.第2页是对章项目的介绍,之后是项目导引、操作要点,以及查阅资料的相关网站的网址,并将在未来学习中会遇到的与完成项目相关的页码都标出来,便于学生整体把握.
“研究整数”这一章的章项目的主题是“公民”,配图是美国国会大厦及议会会议的彩色图片.具体题目是“有得有失”,并配有如下的叙述:在这个项目中,你将绘制一张地图,这张图能直观地显示美国每个州的众议院的议员数是如何变化的.你还需要做一个折线图,并写一些关于这些变化的介绍.你将以海报或小册子的形式展示你的地图、折线图和文字介绍.
项目导引如下:每个州众议院代表的数量根据人口的变化而变化.根据1990年人口普查显示,佛罗里达州增加了4个众议院名额,而宾夕法尼亚减少了2名成员.研究最近一次的人口普查后,每个州的众议员的数目是如何改变的.画出并跟踪能显示每个州情况的地图;把众议院成员减少的所在州标红;把增添了众议院成员的所在州标蓝;成员人数没有变化的众议院所在州保留白色.
操作要点如下:利用互联网找出哪个州的众议院人数增加了,哪个州的众议院人数减少了;使用电子表格记录你收集的数据;使用文字处理机,写下你的关于变化的叙述.
工作过程如下:你可以使用在第十一章学到的知识来帮助你跟踪记录众议院人数的变化.参考教材第433页要求的地图,在每个州写出一个整数,代表众议院的成员数目是如何变化的.为你所在的州和与其相邻的州,分别写一个整数,算出这些整数的总和.你所在的地区有没有获得或失去在众议院的成员?对每一个众议院成员人数有变化的州,在折线图上标注一个有正负的整数.众议院议员总人数的变化是什么?使用下面的清单,以确保你的海报或小册子是完整的.(1)地图清晰易读;(2)折线图正确;(3)讨论众议院变化的叙述包括:你所在的地区是否已经获得或失去了代表,代表的总人数是如何变化的.添加一些修饰,让你的海报或小册子更有吸引力.
2.实用细致的新知学习
介绍完章项目之后,就进入到具体的小节学习之中.每一小节在标题之后,首先给出了具体要学的知识点(What you will learn?),以及何时用到这些知识(When am I ever going to use this?),有的小节还给出关键提示(Word to the Wise).在正文部分,教材首先呈现一个具体的实例,然后介绍要学习的概念和性质,紧接着就是两个具体的例题.根据知识内容的特点,有的小节又接着安排与例题联系紧密的两道例题,有的小节则再安排应用方面的两道例题.
教材第十一章第一节的实例背景是:每年三月,都要举行艾迪塔罗德狗拉雪橇比赛,赛程始于阿拉斯加州的安克雷奇市,止于诺姆市.在这一季节,安克雷奇市白天的平均最高气温是34℉,然而选手们和他们的狗将要面对的最后气温是零下30℉.这一温度你可以写成-30.
新知识介绍什么是整数、正整数、负整数,怎样在数轴上表示整数,然后是四道例题.例1是在数轴上表示-5;例2是在数轴上表示+2.之后是与这两道例题联系密切的两道例题,都是用一个整数表示地理位置;例3要求用整数表示死海低于海平面1 312英尺;例4要求用整数表示珠穆朗玛峰高于海平面29 028英尺.
教材最后又介绍了相反数的概念,接着就是两道例题,分别写出+4和-3的相反数.
3.目标明确的练习题
AC版教材的知识巩固部分分成理解检查和练习两个部分.理解检查又分为数学交流、指导练习和附录参考答案;练习则分为操练、应用和解决问题,以及综合练习.习题中如果有背景,则将背景类型也都一一标出.
第一节的“数学交流”部分有三道题,第1题要求在数轴上明确-1和+2;第2题是先在数轴上表示6和它的相反数,然后再解释为什么这两个数是相反的;第3题是写出一个可以用正整数或负整数表示的实际例子,并解释意义.指导练习则与例题相对应,第4~6题与例1、例2相类似,画出数轴并表示+9,-7和3;第7~8题与例3、例4类似;第9~11题则与例5、例6相类似.最后的拓展知识有两道题,第12题要求描述-10的相反数,第13题则介绍超导材料的温度.
“练习”部分的习题标号延续“理解检查”部分,其中习题的数量明显增多,“操练”部分仿照例题,其中6道题是在数轴上表示数,6道题是描述具体的情境,6道题是写出一个数的相反数.还有3道题是在一条数轴上表示三、四个数.在“应用和解决问题”中有4道题,第39题是地球科学背景,要求表示地球中心的温度是7 000℃;第40题是先表示佛罗里达州的杰克逊维尔市海拔0米,再用整数解释;第43题是章项目的第1题;第44题要求辩证思考,比较数轴和温度计,它们哪里相同,又有什么区别?在“综合练习”栏目中,给出了5道与前面章节学习相关的习题,其中还有一道是标准检测题,主要起到复习的作用.
4.别具一格的“实验室”
为了学习“整数的加法”,教材提前安排了“手工实验室”,帮助学生建立零数对的概念.首先是要求小组一起按照教材中给出的步骤操作,然后再自己独立完成.学生通过小组合作学习的方式完成操作是独立完成的前提.
由于乘法和除法是互逆运算,在学习完乘法运算之后,教材又安排了“头脑实验室”,通过两名学生如何根据比赛时间和训练时间确定训练计划这一实际问题,思考如何利用倒推法想问题.其中解决问题的策略完全按波利亚问题解决的四个步骤进行,最后还逐步拓展到在解决数学问题中是如何操作的.
在这一章中,教材还安排了与职业生涯规划相关的阅读材料,指出了未来要想成为统计学家所应具备的基本能力,鼓励学生学好数学.
在学习第八节“图形变换”之前,教材又一次安排“手工实验室”,要求学生合作完成与图形的平移和图形的翻折相关的基本操作,为在坐标系中画出经过变换后的图形打下基础.
5.系统全面的章复习
在全章的学习结束之后,教材安排了系统的复习.首先总结了这一章出现过的专业术语,如几何方面有坐标网络、坐标系、有序数对(数偶)、原点、象限、x轴、y轴等;在代数方面有正数、负数、相反数、绝对值等;问题解决方面有倒推法等,然后是这些术语在具体问题中的应用.
总结的第二部分是目标、例题和复习.在呈现了每个知识点及出现的位置之后,教材都给出了1道例题和相对应的4道以上的练习题.然后是应用和问题解决,最后是一些可以用来代替的问题.例如,通过解决章项目的问题来检查全章的学习效果.
总结的最后部分是整章的标准检测题,包括选择题和主观题两部分.
三、美国初中数学教材的特点分析及启示
1.丰富的问题背景和大量的实际问题体现出数学学习的价值
无论是章项目的全章学习背景,还是每节课的知识发生、发展的问题情境,还是例题、课堂练习,以及作业中的实际问题,正如这版教材的名字一样,处处体现出数学知识与社会生活、与其他学科的联系与应用.究其原因,是因为其课程标准中既制定了内容标准,又制定了实践标准.内容标准规定了学生应该理解什么、能够做什么,而在实践标准中则明确规定了数学教育者应该致力于学生发展的各种专业技能,包括良好的建模能力,策略性地使用恰当的工具,严谨的表达和交流等.恰恰是因为内容标准与实践标准的并行,才使得数学理解成为学生学习数学的纽带.综观“研究整数”这一章的问题背景,涉及到了体育比赛、建筑历史、游戏娱乐、庆典游行、外国习俗、广播电视、运动训练、民俗传统等八个方面,章中还有职业生涯规划方面的指导.在习题设计中,含有背景的习题共50道,比例接近15%,并且这些背景都是真实的.AC版教材注意与实际背景联系的设计思想,十分值得借鉴.
2.混编的内容设计体现出数学知识结构的灵活性
传统的教材知识逻辑大都按数学知识的学科逻辑进行组织,代数、几何、统计与概率的内容基本上都单独成章、成节.AC版教材不仅在章节的顺序上进行混编,在具体每一章的内容上也是混编的.在“研究整数”这一章中,前6节是“数与代数”领域的内容,学习的是整数的概念,以及加、减、乘、除运算,其中还有倒推学习策略的学习.后3节则是坐标系和平移、轴对称的学习,这属于“图形与几何”学习领域的内容,又体现出整数的应用.这样的设计既有美国数学课程“一英里宽,一英寸厚”的特点,又体现出集中性与连续性的特征,让学生体验到学习数学的整体性,这无疑也是一种有益的尝试.
3.目标明确的习题设计有利于学生自主练习
AC版教材的习题设计有很强的针对性,在每道例题之后,“理解与检查”部分都安排与例题极为相似的练习,用于学生形成技能.不仅如此,“理解与检查”部分还注意引导学生形成自己的理解,要求学生多叙述、多解释、多举例,栏目上明确了“数学交流”和“指导练习”的地位.在“课后练习”中,练习题的数量明显增多,一些简单的变式题也开始出现.而“练习与应用”又一直是习题设计的主线,贯穿于课堂练习、课后作业、单元复习等各个环节.在每道习题前面都明确指出了问题背景的类型,内容涉及科学、经济、物理、统计、几何、营养等各个学科,题目虽然简单,但与化学、生物、地理、经济、物理等多方面的联系都非常密切.除了与社会生活的广泛联系与应用之外,在常规题型的基础上,还有找规律、用自己的话来说等开放性问题,以提高学生的数学交流的能力.“练习”中增设了辩证思考类的习题,引导学生对新、旧知识的冲突形成自我理解.在单元总结中,教材给出了具体学习目标下的例题及其相对应的练习题,增强了练习的针对性.
4.对学生学习方式的培养有重要的作用
接受学习、自主学习、合作学习、探究学习都是数学的主要学习方式.根据学习内容特点的不同,采用不同的学习方式是十分重要的.在例题之后的“理解与检查”中,都是首先引导学生建立自己对知识的理解,通过说一说、写一写、举例子等方式,通过开放题的解决,来引导学生自主学习.AC版教材中几个“实验室”栏目的设计,为学生的合作学习和探究学习提供了很好的素材和机会,而这些学习内容又是未来学习所必须的.例如,学习除法前学习倒推的思考策略,学习图形变换前研究平移与翻折.对于章项目的设计,又给学生提供了完整地经历问题解决的机会,探究活动贯穿于全章学习的始终.

