非结构有限体积耗散格式精度分析

张 亮，艾邦成，陈 智

(中国航天空气动力技术研究院，北京 100074)

在计算流体力学领域，非结构有限体积方法由于其优异的复杂外形适应性在各类武器型号设计中得到了广泛的应用。在非结构数值模拟技术中，对流格式、限制器以及隐式迭代方法等均得到了广泛的研究，但针对黏性项离散的耗散格式长期以来并未得到足够的重视。近年来，随着精细化数值模拟需求(气动加热、摩阻以及分离流高精度模拟)的不断提升，非结构有限体积耗散格式逐渐成为重要的研究方向。

在有限体积方法框架内，构造耗散格式的核心在于确定界面处的流动梯度。由于黏性项天然的椭圆特性，耗散格式构造需要满足离散极值原理以避免“奇偶失联”及数值稳定性问题[1-2]。对于结构网格，由于其规则的方向特性，一般可基于当地计算坐标系直接采用中心格式计算界面梯度[3]。而对于非结构网格，由于计算网格的无序性，中心型耗散格式难以应用，常用的处理方法是借鉴结构网格中的“薄层”简化思想[4]，将界面梯度沿主方向和次方向进行分解，对不同方向的梯度采用不同方法进行计算[5-10]。在实际应用中，Edge-Normal格式[7]和Face-Tangent[8]格式得到了更为广泛的采用。相比较而言，对于存在较大扭曲的计算网格，Face-Tangent格式具有更好的数值稳定性[11]。

与传统耗散格式构造方法不同，Nishikawa基于一维双曲系统提出了一类新型alpha-damping耗散格式[12]。该格式由相容项和阻尼项两部分组成，其中相容项用以保证格式的数值相容性，阻尼项用于抑制高频误差的发展。Nishikawa还进一步证明了包括Edge-Normal格式和Face-Tangent格式在内的多种耗散格式均可等价或近似等价于具有不同高频阻尼的alpha-damping格式。Jalali等针对大量非结构有限体积耗散格式开展了计算精度及数值稳定性研究，结果表明采用优化高频阻尼系数的alpha-damping格式具有最优的数值表现[13]。

Nishikawa提出的alpha-damping格式为不同耗散格式建立了一个统一框架，因此对于非结构有限体积耗散格式的构造具有重要意义。但其理论分析是基于均匀网格和固定中心梯度格式，非结构网格以及不同梯度格式条件下高频阻尼对计算精度的影响并不明确。本文借鉴alpha-damping格式相容项和高频阻尼项结合的构造形式，采用一维非均匀网格模拟非结构网格几何特征，通过对模型方程的理论分析和数值试验，研究高频阻尼系数在不同梯度格式条件下对耗散格式精度的影响规律。

1 耗散格式理论分析

1.1 格式精度分析

考虑一维耗散模型方程：

ut=uxx

(1)

(2)

(3)

对于线性重构有：

(4)

不同于原始alpha-damping格式，为表征网格非均匀特性的影响，这里采用加权平均方法计算相容项部分，同时高频阻尼系数也定义为当地值。

将式(3)和式(4)代入式(2)并整理可得：

(5)

在实际计算中，需要采用梯度格式近似计算单元梯度，这里采用2阶精度梯度格式：

(6)

将式(6)代入式(5)并在xj处进行泰勒展开可得修正方程：

(7)

其中：

c0=0

c1=0

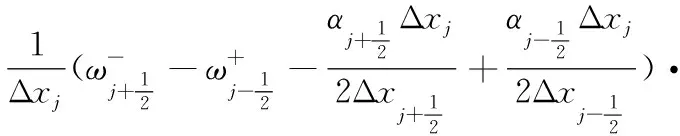
需要强调的是，这里的分析结果仅严格适用于2阶及高于2阶精度的梯度格式。对于1阶精度梯度格式，相容性分析结果则与梯度格式具体的截断误差形式相关。

1.2 梯度格式影响分析

Nishikawa指出，当α=4/3时，alpha-damping格式在均匀网格条件下可达到4阶精度[12]。虽然该优化系数由2阶中心梯度格式推导得到，但其在后续的复杂多维问题及NS方程扩展中均得到了广泛的应用[14-16]。为确定α=4/3取值的普适性，这里针对一般梯度格式给出高频阻尼系数最优值与梯度格式之间的定量关系。

考虑一般梯度格式：

在均匀网格条件下，式(7)各项的系数可做进一步简化：

c0=0,c1=0,c2=1,c3=(1-α)a1Δx

c4=[(1-α)(a2+1/6)+α/12]Δx2

显然，对于均匀网格，格式(3)自动满足相容性条件。当α=1时，修正方程截断误差可至少保证2阶精度。当α≠1时，1阶精度梯度格式仅能保证1阶精度截断误差，2阶精度梯度格式至少可保证2阶精度截断误差。为实现2阶精度以上的截断误差，需要满足c4=0，即：

(8)

显然，可实现更高精度的高频阻尼系数最优值取决于梯度格式的2阶截断误差系数。

对于2阶精度中心梯度格式(6)，有a2=1/6，因此高频阻尼系数最优值为α=4/3。由于该格式同时满足a3=0，因此格式最终可实现4阶精度。

对于a2≠1/6的2阶及高于2阶精度的梯度格式，高频阻尼系数最优值需由式(8)确定。特别的，对于高于2阶精度的梯度格式有a2=0，因此高频阻尼系数最优值为α=2。对于一般情况a2∈[0,+∞)，有α∈(1,2]，见图1。

2 算例测试

2.1 一维算例

针对一维泊松方程uxx=S开展算例测试。选择解析解u=sin(πx)，对应源项S=-π2u。计算域取为x∈[0,1]，函数分布曲线如图2所示。

计算网格采用均匀网格、随机网格和拉伸网格3种类型，每种网格类型的单元数分别取10，20，40，80。

采用3种梯度计算格式：

对于均匀网格，g1和g2等价，均为2阶精度。对于非均匀网格，g1为1阶精度，g2为2阶精度。g3为解析解，可认为是无穷高阶精度。

对于相容项的加权系数，大量数值试验表明采用代数平均和基于距离的线性加权平均均可实现较高的计算精度，且两者差异并不显著[13-17]。结合前文关于非均匀网格的相容性分析，这里选择代数平均进行相容项梯度加权。

2.1.1 均匀网格

均匀网格的单元尺寸分布特征如图3所示。

图4～图5给出了采用不同梯度格式时，高频阻尼系数对均匀网格数值精度的影响。由于g1和g2在均匀网格下等价，这里仅给出g1的计算结果。

对于g1，高频阻尼系数α=4/3时，截断误差和离散误差实现了4阶精度，其他高频阻尼系数仅能实现2阶精度。而对于g3，高频阻尼系数α=2时，截断误差和离散误差实现了4阶精度，其他高频阻尼系数仅能实现2阶精度。这一结果与本文的理论分析一致。

2.1.2 随机网格

随机网格单元i的网格尺度ΔxR,i=ZFi·ΔxU，其中ΔxU=δmax/N为等效网格尺度，N为网格单元数，δmax为计算域长度，ZFi为单元i处的随机缩放因子，本文限制ZFi∈[0.8,1.2]。网格尺度分布特征如图6所示。

图7～图9给出了采用不同梯度格式时，高频阻尼系数对随机网格数值精度的影响。

对于截断误差，当α=1时，3种梯度格式均近似实现了1阶计算精度。其中，g1由于梯度计算精度低于2阶，在较密网格时截断误差精度有所损失；g2和g3由于严格满足2阶梯度计算精度，截断误差精度至少达到了1阶。而对于其他高频阻尼系数，格式无法实现相容性。这一结果与前文的理论分析是一致的。

对于离散误差，不同梯度格式以及不同高频阻尼系数均实现了近似2阶计算精度，但高频阻尼系数对离散误差绝对值的影响在不同梯度格式条件下表现不同。其中g1和g2在α=4/3时具有最小的离散误差，而g3在α=2时具有最小的离散误差。这说明，非均匀网格条件下产生最小离散误差的高频阻尼系数与式(8)确定的均匀网格最优值一致。

2.1.3 拉伸网格

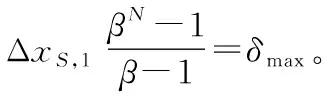
图11～图13给出了采用不同梯度格式时，高频阻尼系数对拉伸网格数值精度的影响。

对于截断误差，不同梯度格式以及不同高频阻尼系数均实现了格式的相容性。为解释这一现象，可考虑式(7)中的相容性条件。在拉伸网格条件下，采用代数梯度加权的相容性条件可简化为

显然，当ΔxU趋近于0时，β趋近于1，因此c2趋近于1，格式相容性得到间接满足。由于拉伸网格光滑性较好，截断误差的高阶项可实现较好的相互抵消，因此截断误差精度优于理论分析结果。

对于离散误差，不同梯度格式以及不同高频阻尼系数均实现了近似2阶计算精度。与随机网格相同，高频阻尼系数对离散误差绝对值的影响在不同梯度格式条件下表现不同，产生最小离散误差的高频阻尼系数与式(8)确定的均匀网格最优值一致。

2.2 多维算例

采用3种梯度计算格式：g1为高斯梯度格式；g2为距离加权最小二乘梯度格式；g3为梯度解析解。相容项仍然采用代数平均方法进行加权。

1) 均匀四边形网格

计算域为x∈[0,1]，y∈[0,1]，x和y方向的波数为nx=1，ny=1，网格尺度分别为1/10，1/20，1/40和1/80。典型计算网格及计算结果如图14所示。

图15～图16给出了采用不同梯度格式时，高频阻尼系数对数值精度的影响。由于在均匀四边形网格条件下，g1与g2均等价于二阶中心格式，因此这里仅给出g1的计算结果。

可以看到，与一维均匀网格计算结果相同，g1和g3分别在其对应的高频阻尼系数最优值时实现了4阶计算精度，而其他高频阻尼系数仅能实现2阶计算精度。

2) 均匀三角形网格

计算域为x∈[0,1]，y∈[0,1]，x和y方向的波数为nx=1，ny=1，计算网格采用对角化技术生成，平均网格尺度分别为1/10，1/20，1/40和1/80。典型计算网格及计算结果如图17所示。

图18～图20给出了采用不同梯度格式时，高频阻尼系数对数值精度的影响。

对于截断误差，由于g1和g2均无法严格满足2阶梯度计算精度，因此截断误差无法实现相容性。尤其对于g1，截断误差与网格尺度出现了负相关，格式不相容性更为严重。g3由于严格满足2阶梯度计算精度，截断误差在α=1时达到了1阶精度。

对于离散误差，g1仍然无法满足格式相容性。g2和g3则均实现了2阶计算精度，且其产生最小离散误差的高频阻尼系数与式(8)确定的均匀网格最优值一致。

3) 拉伸四边形网格

计算域为x∈[0,1]，y∈[0,0.05]，x和y方向的波数为nx=1，ny=20，计算网格在x方向等距分布，y方向由2.1.3节的拉伸方法得到，压缩因子CF取为100。x和y方向的网格单元数分别为10，20，40，80。典型计算网格及计算结果如图21所示。

图22～图24给出了采用不同梯度格式时，高频阻尼系数对数值精度的影响。

对于截断误差，与一维拉伸网格算例相同，由于网格的光滑性，不同梯度格式以及不同高频阻尼系数均实现了2阶计算精度。

对于离散误差，与前文算例相同，不同梯度格式产生最小离散误差的高频阻尼系数仍然与式(8)确定的均匀网格最优值一致。

3 结论

1) 对于非均匀网格，在采用2阶精度梯度格式条件下，采用代数平均加权的相容项和α=1的高频阻尼项是保证耗散格式严格相容的必要条件。对于光滑的非均匀拉伸网格，由于局部误差的相互抵消，格式相容性有较大改善。采用低于2阶精度的梯度格式会降低格式的相容性。

2) 均匀网格条件下高频阻尼系数最优值与梯度格式的2阶截断误差系数相关，不同梯度格式应对应不同的高频阻尼系数最优值。在非均匀网格条件下，采用均匀网格最优值的高频阻尼系数可得到更小的离散误差。

本文研究工作虽然基于一维理论模型，但研究结论对于多维问题仍具有一定指导意义。但由于耗散格式精度与梯度格式紧密相关，而多维梯度重构不同于一维梯度重构，其受重构算法及具体网格特征的影响巨大，因此后续研究重点将集中于多维情况下不同梯度构造格式的精度特性分析，并以此为基础深入开展多维耗散格式精度及相容性研究。