逆幂律模型下Frechet分布序进应力加速寿命试验的统计分析

何 亮，徐晓岭

(上海对外经贸大学 统计与信息学院，上海 201620)

随着科技的不断发展，产品更新换代速度加快，电子设备及元器件的可靠性在不断提高，一般的产品寿命试验方法已经不再适用。所以通常设计加速寿命试验对高可靠性、长寿命的产品的寿命进行快速评定。序进应力加速寿命试验(简称序加试验)是加速寿命试验中的一种重要方法，试验中受试产品的应力水平随时间连续上升，是时间的连续非降函数，相比于恒定应力加速寿命试验能缩短试验时间。

由Frechet在1927年提出的Frechet分布[1]在各种工程应用的统计建模中非常重要，在极端气候事件中也有相当广泛的应用。Mann在文献[2]中讨论了Frechet分布及Gumbel分布间关系与其参数估计。Longin在文献[3]中将Frechet分布运用到拟合股市的极端价格变动下的走势。Nadarajah在文献[4]将Frechet分布用于社会学模型。Zaharim等在文献[5]中将对数正态分布以及Frechet分布用于风速数据的预测分析中。Abd-Elfattah在不同的标准下对广义Frechet分布进行了拟合优度检验[6]。Mubarak在文献[7]中给出了逐步增加定数截尾场合下(移除数量服从二项分布)的参数极大似然估计以及区间估计。Abbas和汤银才在文献[8]中对已知形状参数的Frechet分布进行Bayes估计，在[9]中研究了在定数截尾数据场合下参数的极大似然估计以及最小二乘估计。国外的很多学者对一般化的Frechet分布有较多的研究，Nadarajah与Kotz在文献[10]中提出指数化的Frechet分布，与Gupta提出Beta-Frechet分布[11]。Krishna在文献[12]介绍了Marshall-Olkin Frechet分布。Afify提出Weibull-Frechet 四参数寿命分布模型[13]，并通过极大似然估计其模型参数。Mansoor等引入扩展的四参数Frechet分布，亦称指数化的指数Frechet分布，并与Marshall-Olkin Frechet分布、指数Frechet分布、Frechet分布基于实际数据作比较，说明了新分布更加贴合这些数据[14]。在加速寿命试验方面，Shahab在文献[15]中基于指数过程在常应力下给出分布的参数估计以及区间估计，在[16]中通过图像研究Frechet 分布简单步加试验的最优时间。Ghaly在文献[17]中在常应力下对指数分布族加速寿命试验的不同方法进行了对比，并基于实际数据给出模型选用的建议。

本文基于逆幂律模型对Frechet分布在与时间为一般线性关系的序进应力下的加速寿命试验进行统计分析，分别运用极大似然估计、MPS估计以及最小距离估计分别给出参数的点估计，并通过大量的Monte-Carlo模拟对比3种估计方法的精度。

1 基本假设

统计分析基于以下几个假设：

假设1 在恒定应力V>0下，产品寿命X服从Frechet分布，记为X～Fr(α,β(V))，其分布函数为：FV(t)=exp{-(β(V)/t)α}，其中α>0为形状参数，β(V)>0为尺度参数。

假设2 不同应力水平下，产品的失效机制相同，即形状参数α保持不变。

假设3 特征寿命β(V)与应力V满足逆幂律模型：β(V)=1/(dVc)，其中d>0,c>0为待估参数，且独立于应力V,φ(V)为已知函数。对模型两边取对数，可得到β(V)满足对数线性关系：lnβ(V)=a+bφ(V)，其中a=-lnd,b=-c,φ(V)=lnV

假设4 产品的剩余寿命仅依赖于当时已累积失效部分及当时的应力水平，与累积方式无关，此即Nelson假定。数学表达为：在应力水平Vi下产品连续工作ti时间的累积失效概率Fi(ti)相当于该产品在应力水平Vj下工作tj时间的累积失效概率，即Fi(ti)=Fj(tj)。

在序加试验中，将n个产品置于序进应力V(t)=Kt+V0(V0≥0)下进行加速寿命试验，直至所有受测样本失效为止。关于在此应力下的产品寿命分布，有如下定理。

定理1 若产品寿命满足上述基本假设，当应力为关于时间的函数，即产品寿命在应力V=V(t)下的分布函数为：

(1)

当ξ→0时，由Riemann积分的定义并由假设3有β[V(t)]=exp{a+bφ[V(t)]}，则在应力V(t)下产品寿命的分布函数为：

2 逆幂律模型下序进应力加速寿命试验的统计分析

2.1 极大似然估计(方法1)

根据定理1，产品在应力V(t)=Kt+V0(V0>0)下寿命的分布函数和密度函数为

(2)

(3)

试验得到的产品失效数据为t(1)≤t(2)≤…≤t(n)。

其似然函数为

对数似然函数为

lnL=nlnα-nαlnd+n(α+1)lnK+

分别令对数似然函数对α,d,c求导：

2.2 MPS估计(方法2)

在极值分布的参数估计中，小样本场合下的极大似然估计稳定性较差，而相比之下由Cheng和Amin提出的MPS估计具有更稳定的估计结果[20-21],甚至能在某些极大似然估计失效的情况下仍能作出良好的评估[22]。

在序进应力V(t)=Kt+V0下，产品寿命次序统计量T(i)的分布函数记为FT(i)(t)，取值为t(i)，则有

FT(i)(t)=IF*(t)(i,n-i+1),i=1,2,…,n

(4)

其中当i=1,2,…,n时，

[1-(1+c)ln(Kt(i)+V0)]}·

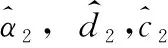
2.3 最小距离估计(方法3)

Wolfowitz提出了最小距离估计(或称拟合优度估计)[24-25]，并证明了估计的一致性。其思想是通过使经验分布与某些参数族分布的距离达到最小。常用的距离准则有卡方距离、Kolmogorov-Smirnov (K-S) 距离、Anderson-Darling (A-D) 距离以及Cramer-Von Mises (CVM) 距离。本文选取Anderson-Darling (A-D) 距离作为拟合优度统计量。

经验分布函数Fn(t)与分布函数F(t)的距离记为EDF统计量，即：

(5)

其中ψ(t)为权重函数。令ψ(t)={F(t)[1-F(t)]}-1，为方便计算，A-D统计量的代数形式如下：

(6)

其中z(i)=F(t(i)),i=1,2,…,n,t(i)为第i个次序统计量的值，令

3 数值模拟

针对真值为α=0.5,1,1.5,d=1,c=1,样本容量为n=20,30,50,在序进应力V(t)=t+1下分别进行 50 000次的Monte-Carlo模拟试验，试验结果如表1所示。

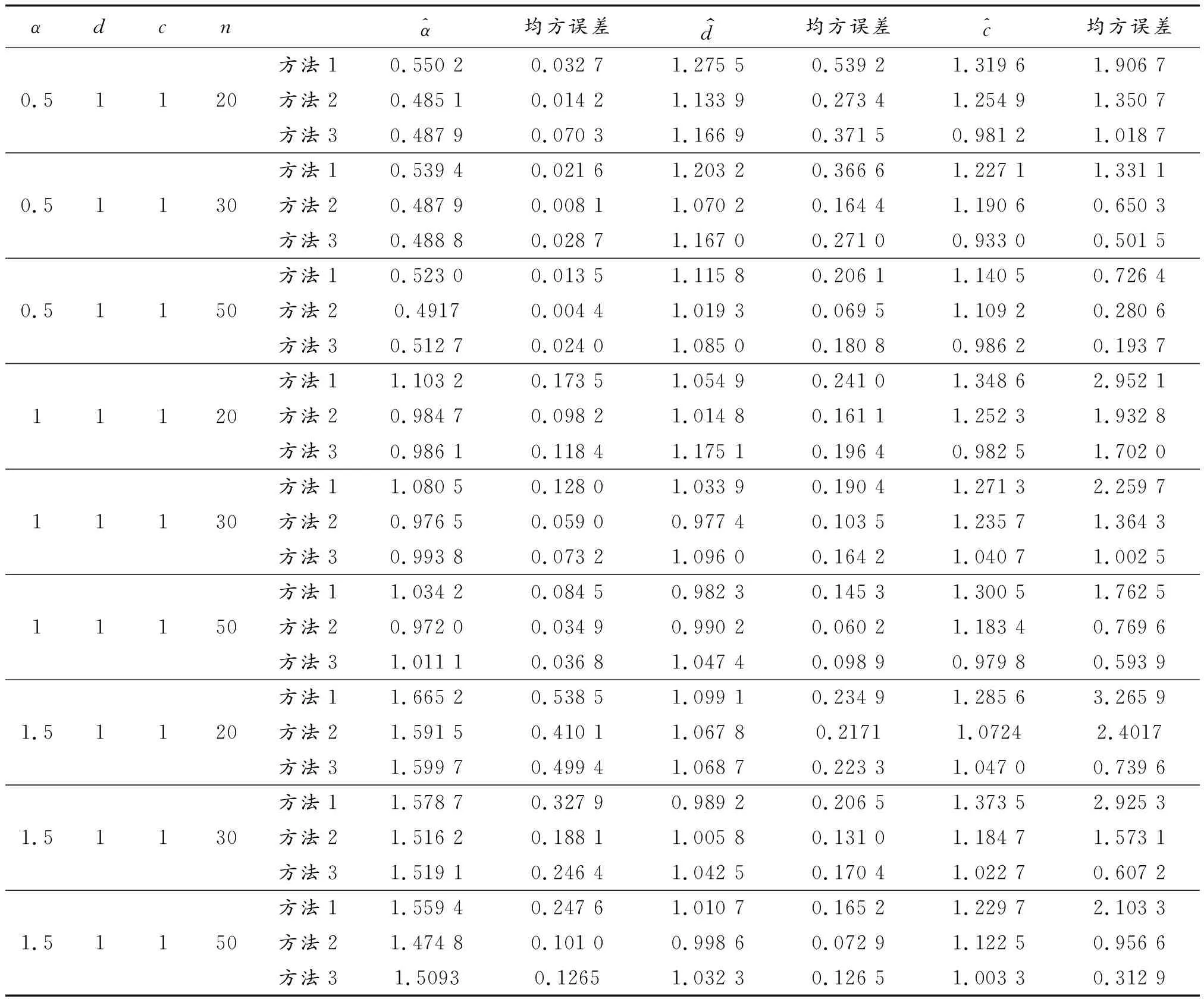
表1 序进应力为V(t)=t+1下Monte-Carlo模拟试验结果

从表1中的结果，可以得到如下结论：

1) 关于参数α，就均方误差意义上而言方法2的效果最好。当α较小(<1)时，方法3误差大于方法1，但估计均值更加接近参数真值；当α≥1时，方法3的误差介于方法1和方法2之间，且估计均值较方法1、方法2更接近真实情况。

2) 关于参数d，方法2的估计效果最好。方法1的误差在3种估计方法中最大，而当α=0.5时其估计均值离真值最远，当α=1,1.5时较方法3而言更接近真值。

3) 关于参数c，方法1的估计均值离真值较远，也最不稳定；方法2效果次之，方法3效果最佳，甚至在小样本情况下仍能得到较好的估计结果。

在实际应用中，应通过方法2(MPS估计)得到参数α,d的估计值，通过方法3(最小距离估计)得到参数c的估计值，以达到最佳的估计效果。下面给出模拟算例。

模拟算例：取真值为α=1,d=1,c=1，在序进应力V(t)=t+1下进行序加试验，利用Monte-Carlo模拟生成30个产品失效数据如下：

0.238 50.293 40.325 40.361 70.385 00.445 70.470 40.486 30.546 70.610 30.668 70.772 20.803 70.917 50.941 80.970 50.993 51.009 61.048 31.074 61.143 91.514 11.519 91.659 52.27162.892 02.958 73.098 73.90 749.294 2