火控雷达组合欺骗式干扰研究
张宏伟,冉宏远
(陆军工程大学 石家庄校区,石家庄 050000)
火控雷达是现代防空武器系统的关键部分,其主要作用是实现目标的精确跟踪和火力控制。对火控雷达实施高强度、有针对性、多样式的电磁干扰,是提高突防概率、破坏防空体系的重要手段。由于火控雷达对目标的测量具有很高的精度,以往都是利用单部干扰机对其干扰,对火控雷达的一维或者二维参数进行欺骗,或者直接采取压制性干扰。但是三维参数精确化的欺骗式干扰,实现相对困难。随着现代战争中的电磁环境越来越复杂,飞机的作战水平和生存能力需要大大提高,本文的应用背景是飞机两机翼上各搭载一部干扰机,对单脉冲火控雷达实施三维参数的欺骗式干扰。
1 火控雷达干扰分析
1.1 火控雷达实施干扰的特殊性
对于雷达的干扰样式主要有遮盖式干扰和欺骗式干扰。遮盖式干扰是利用噪声或类似噪声的干扰信号或压制回波信号,在雷达显示器上形成强杂波背景或大量假目标回波,使雷达的探测能力降低,此类干扰样式主要应用于干扰搜索和引导雷达;欺骗式干扰是采用假的目标或目标信息作用于雷达的目标参数、参数测量和跟踪系统,使雷达发生严重的虚警,或者不能正确地测量和跟踪目标参数,欺骗样式主要有角度、距离、速度和假目标欺骗等,欺骗式干扰主要应用于干扰火控雷达。
1) 最大信号法测角系统。该测角方法精度不高,不能用于自动测角,在搜索和引导雷达中应用较为广泛;
2) 圆锥扫描自动测角系统。该测角方法可以通过对信号导相的方法来实现角度欺骗,但是目前这种测角系统的雷达并不多见,而且测角精度不高。
3) 单脉冲自动测角系统。该测角方法目前广泛应用于火控雷达中。单脉冲自动测角系统具有测角速度快,测角精度高等特点,而且不易被干扰。目前,利用单个干扰机对单脉冲测角系统实施精确化的角度欺骗难度较大,利用双干扰机的密切配合,才会产生精确化的角度欺骗[1]。
1.2 针对火控雷达的常用干扰策略
1) 角度欺骗干扰
反向交叉眼技术是利用双干扰机的功率和双信号的相位不同,对单脉冲雷达的测角系统实施欺骗[2],如图1所示。
θ为雷达测得的角度与真实目标角度的差值,G1和G2分别为双干扰机发射信号增益,θe为雷达与双干扰机中部连线和雷达与干扰机连线的夹角,Δθ为双干扰机与雷达连线的夹角,Δφ为天线2发射信号相位改变量,L为双干扰机之间的距离,R为双干扰机中部连线距离雷达距离,β=G2/G1,Δθ=2θe。
依据文献[2]得:
(1)
对式(1)仿真可得如图2所示。
取Δφ=180°,进行有规律的变化β,可以产生角度欺骗。
2) 距离欺骗干扰
雷达距离欺骗干扰的工作基本原理为干扰机接收雷达信号,对雷达信号进行有规律的延时,再由干扰机发出[3]。
3) 速度欺骗干扰

以上的干扰分析都是基于欺骗火控雷达单维目标参数的,部分干扰机也有把距离-速度组合进行同时欺骗的[5]。如果单独实施距离欺骗、速度欺骗或者距离-速度组合欺骗,虚假目标的角度没有改变,火力一旦实施射击,目标仍有被击中的可能性。如果单独实施角度欺骗,假目标就有一个角度信息是错误信息,不利于保护真实目标[6]。
针对以上分析的当前干扰策略的不足,本文提出了一种距离-速度-角度三维参数的组合欺骗式干扰的实现方法,利用该方法可以更好的对火控雷达实施欺骗式干扰,更有利于保护真实目标。
2 三维参数组合欺骗式干扰数学建模
对距离-速度-角度三维参数的组合欺骗式干扰建立数学模型时,为了便于分析,按照先分解,后结合的思路进行。首先对距离-速度二维参数欺骗干扰进行建模,用该模型和角度欺骗模型进行有机组合,完成三维参数的组合欺骗式干扰数学建模。
2.1 二维参数组合欺骗式干扰数学建模
干扰机对截获的雷达信号进行延时处理,每隔Tj的时间对信号进行一次延时改变,每隔Tj的延时改变量为tj,tj为延时步进步长,Tj为步进时间间隔,fj为在Tj时间内对转发信号的固定频率量,vj为假目标相对于真实目标的速度[7]。
则有下式成立:
(2)
对雷达信号在时域内和频域内进行调制时,Tj、tj、fj需要满足以下关系:
(3)
将式(2)式代入式(3)式可得:
(4)
雷达信号的载波频率为f0。
距离-速度组合欺骗干扰过程实现过程:每隔Tj的时间段,对信号进行一次延迟处理,延时量为tj,则,第m次步进延时时,现实真实的时间为m×Tj,信号的延迟量为m×tj,在频域内,对信号的多普勒频率的变化量为fj[8],如图3所示。
在二维参数组合欺骗式干扰模型基础上,融合角度欺骗理论,建立三维参数组合干扰建模。其原理为:对信号进行时间延迟,产生距离欺骗;多普勒频率改变,产生速度欺骗,同时调整双干扰信号的相位和功率(本文统一规定一路信号相位调整180°,另一路信号相位不变),产生角度欺骗[9]
2.2 距离-速度-角度三维参数组合欺骗式干扰数学建模
飞机以航路捷径为0 m,高度不变的姿态,匀速水平飞向雷达。想要获得一个与真实目标速度有角度偏差的虚假速度,则首先需要对假目标速度进行分解。
如图4所示,假目标速度分解为两个速度分量,径向速度v1,切向速度v2。
径向速度可以依据式(4)分析,利用距离-速度欺骗干扰实现方法产生。切向速度可利用式(1),改变β值,产生虚假匀速[10]。
若虚假目标匀速分行,则径向速度v1和切向速度v2均为恒值。如图5所示。
v1为恒值,则满足式(4)即可;tj为延时步进步长,Tj为步进时间间隔,即在时域内对雷达信号进行延时处理时,每隔Tj的时间对数字信号进行一次延时改变,每隔Tj的延时改变量为tj;fj为在Tj时间内对转发信号的固定频率量;每隔Tj时间,虚假目标在径向上飞出的距离都是相等的,即
s1=s2=s3…=sk
同时v2也为恒值,每隔Tj时间,虚假目标在切向上飞出的距离都是相等的,即
l1=l2=l3…=lk
若要保持上式相等,依据反向交叉眼原理分析可知,每隔Tj的时间,产生的虚假角度变化量是不一样的,即:
α1≠α2≠α3…≠αk

Rk=R0+(v1-v3)TjK
则有下式成立:
θk为β经历过K次变化后,产生的欺骗角度。
由式(1)得:
(5)
Δθk为双干扰机与雷达之间的夹角,L为双干扰机源之间的距离,第K次对信号延时,飞机距离雷达的距离为R0-v3TjK
(6)
将(5)式代入(6)式化简得
(7)
因此,若要满足距离-速度-角度三维参数的组合欺骗式干扰,则需要建立以下数学模型:
(8)
3 三维参数组合欺骗式干扰仿真分析
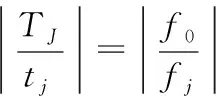
当延时步进时长tj为定值(40 ns)时,对转发信号的多普勒频率改变量越大,则需要的步进时间间隔Tj越小,二者成反比。
当取干扰信号频移量fj为4 kHz时,步进时间间隔Tj为40 ms,并且延时步进时长tj为40 ns。此时,对式(8)中的前3个等式进行仿真,得出β的数值大小(表1)。

表1 仿真参数
如图6所示:对距离-速度-角度三维参数组合欺骗式干扰的实现过程描述如下:飞机双机翼上各搭载一部干扰机,对火控雷达实施干扰。干扰开始后,信号逐次步进,每次步进时,信号频移量fj为4 kHz(该数值为恒定值,步进过程中不累加),步进时间间隔Tj为40 ms,延时步进时长tj为40 ns(该数值为累加值,每步进一次,延时累加一次),根据步进次数的不同,双干扰机功率比β是不同的,具体β的数值可由式(8)计算得出,图7为信号步进间隔次数与相应步进次数β值的仿真图。
对式(8)的Δβk进行分析
Δβk=βk-βk-1
(9)
对式(9)仿真可得图8所示的结果。
由图8可知,随着步进次数的增加,每次β的变化量越来越小。由式(3)得:虚假目标相对于飞机在径向上的速度分量v1=150 m/s,虚假目标相对于飞机的速度v=300 m/s。图9为距离-速度-角度三维参数组合欺骗式干扰的示意图。概略描述了真实目标、虚假目标和雷达的相对关系。
假目标距离-速度-角度三维参数的组合欺骗式可成功实现,在等步进时间间隔下,对信号进行等量延迟,每次步进时,两干扰机的功率比是变化的,并且功率比的变化量越来越小,在干扰全程对信号多普勒频率的改变量为恒定值。
4 结论
基于单维参数的欺骗式干扰理论,对火控雷达实施距离-速度二维参数欺骗式干扰实现较为容易,对于距离-速度-角度的三维参数欺骗式干扰实现相对复杂。通过研究论证分析,得出具体实现方法。

