关于“圆的周长”教学设计的一些思考

徐燕梅

摘要：小学数学作为小学教育的重要组成部分，教师必须重视对数学教学内容的设计，同时提高教学的有效性。本文以“圆的周长”教学设计为例，并从三个方面入手，探讨了如何提高“圆的周长”的教学质量，以供同仁参考。

关键词：小学数学  圆的周长  教学设计

通过听取多位不同教师对于“圆的周长”课程的教学，笔者发现，大部分教师在讲解“圆的周长”这一节课时，普遍存在一些问题。基于此，结合自己在课堂上的一些教学经验，笔者对“圆的周长”教学设计提出了自己的一些思路。

在教学“圆的周长”时，大部分数学教师会让学生运用各种途径来测量圆的周长，但这样的教学方式比较麻烦，且具有局限性。对此，笔者经常思考怎样才能快速地教会学生测量圆的周长。经过实践笔者认为，数学教师可以从以下几方面入手：

首先，在学生第一次进行测量圆的周长时，教师要明确这个教学内容的价值在哪里？因为帮助学生掌握操作技巧显然不是数学课上需要重点解决的问题，教给学生所学知识的实际价值才是教学的重点。

其次，在进行圆的周长的测量时，直接测量的方法比较麻烦，且有局限性，所以教师应该考虑其他测量方法，以便让学生掌握测量圆的周长的简单方法。同时，教师要让学生在课堂学习中主动地接受知识，而不是被动地由教师进行灌输式教学。

为寻求更简便的测量方法，笔者深入思考“圆的周长可能跟它的什么有关系？”“圆的周长是不是与直径有倍数关系？”等问题，对此，笔者对这节课进行了重新设计，并在上虞市区域性教研活动中进行了示范教学，最终取得了良好的教学效果。

一、估计周长，体验圆周率

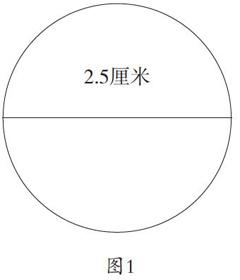
在巩固“圆的周长”这一概念之后，笔者在多媒体课件上出示了一枚硬币及其直径长度（如图1所示），然后提问：这枚硬币的直径是2.5厘米，大家来猜一猜，它的周长是多少厘米？然后投影出示图片：

图1

有的学生说：“我猜圆的周长是5厘米，上面那条弧线大约是2.5厘米，下面那条弧也是2.5厘米，所以周长是5厘米。”有的学生反对说：“我觉得不太对，那条弧线应该比直径长，所以周长应该比5厘米长一点。”也有的学生提出：“周长一定超过直径的两倍，两点之间线段最短，那条弧线一定比直径要长。”这时候，笔者继续提问：“那大家猜一猜，圆的周长可能会是直径的几倍呢？”绝大部分学生的答案都集中在两倍多。通过这样的问答，大大激发了学生的探究兴趣，他们都想要知道，圆的周长究竟是直径的多少倍？

二、探究内化，确认圆周率

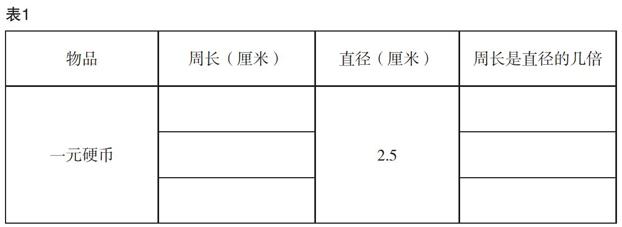
有了前面的铺垫，学生对下面进行实际测量圆的周长的教学就会产生兴趣，并且能够积极主动地参与其中。这时，笔者只需让学生在课堂上进行圆的周长的测量，并将所测量的值除以直径，然后填写在表格中（如表1所示）：

通过测量计算，学生得到的结果都在“三倍多一点”这一范围内。

经过探究，学生得出了圆的周长是直径的三倍多，所以笔者在这个基础上告诉学生，所有的圆都是“周长是直径的三倍多一些”，然后引出圆周率的概念。但是，以这种方式引出圆周率学生能接受吗？为此，笔者对学生进行了分组抽查，并提出问题：“如果是另外的一个圆，这个圆很大或者很小，那么圆的周长还是直径的三倍多一些吗？”结果有三组学生认为不是。

这个统计结果让笔者在“圆的周长”教学中发现了一个需要思考的问题：如何让学生确认周长与直径的比值是固定的？是不是可以让学生测量更多的圆？特别是让那些对这个问题存在疑问的学生进行测量。在第二次探究的时候，笔者不仅给学生提供不同的圆，还允许学生测量自己准备好的圆，以及教室里它能找到的圆，最后将结果交给笔者记录下来（如表2所示）：

最后，通过实际的测量，学生得出结论：圆的周长总是直径的三倍多一些。

三、回顾历史，灌输圆周率

当学生通过多次操作和计算后知道“圆的周长是直径的3倍多一些”，笔者会趁机对学生说：“关于圆的周长是直径的多少倍问题，长久以来一直吸引着无数人对它进行研究。在我国的《周髀算经》中就提到过：‘圆的周长是直径的三倍多一些吧;到公元前3世纪，古希腊的阿基米德则明确说：‘3.14倍多一些吧。;然后，祖冲更精确地说：‘是3.1415926倍多一些。到了现在，依然还有很多科学家在研究圆的周长和直径之间的倍数关系，且越来越精确。研究人员将圆周率计算到了小数点后第12411亿位，12411亿位是什么概念呢？简单地说，如果你一秒钟读一个数的话，读4万年也读不完。”

笔者还告诉学生，对于圆的周长是直径的多少倍的研究，先人们陆续花了几千年的时间，有人甚至付出了毕生的努力，终于达成了这样一个共识，无论是大圆还是小圆，任意一个圆，它的周长除以直径的商都是一个固定的值，我们现在就把圆的周长除以直径的商叫作圆周率，用希腊字母π表示。这个圆周率有两大让人不可思议的特点：第一，这个数是固定的，但是无限的，永远也数不完;第二，这个数不循环，没有规律可循。

科学家永远无法从实践操作中得出圆周率的精确答案，但他们可以提供一個越来越接近的答案，这样可以让学生从历史中感受到探究知识的艰难，感受到圆周率这一数值的来之不易，以及它的独特魅力。不仅如此，让学生知道圆周率这一知识点的重要性，有利于他们今后学习与圆有关的知识。

四、结语

整堂课下来，因为有猜测作为学习的基础，并且在测量、探究中无形中调动了学生的学习积极性和学习知识的欲望，有效提高了课堂的教学效率。

圆周率是一个简单的概念，笔者通过整整一节课的时间进行探究，如在一节课中，教师需要关注哪些细节？对这些细节教师该如何把握？如何营造良好的课堂氛围？笔者还发现，如果一节课的整体逻辑不够清晰，那么在课堂上，学生很难展现自己的活力。所以，笔者通过让学生自己测量，在实践中慢慢摸索，给学生创造了一个良好的学习氛围，让学生主动学习了圆周率这一概念。

学生只有通过亲身动手操作后，才能感受到学习的快乐。整节课上，学生始终都沉浸在浓浓的数学研究氛围中，所有的猜测、操作、测量、计算、归纳、验证等环节都来自于学生的好奇心和主动的求知欲，而这就是笔者所想追求的理想课堂。

参考文献：

[1]马元魁，张天平，张丽丽.无穷级数引入的教学设计[J].高等数学研究，2016，（3）.

[2]盛男.《圆的周长》教学设计[J].中国校外教育，2014，（10）.

[3]游家水.从学生认知水平入手 用矛盾运动规律教学——《圆的周长》的教学设计与思考[J].教育导刊，2014，（1）.

[4]张瑞娟，李桂梅.谈谈《圆的周长》的教学设计[J].黑龙江教育，2001，（Z1）.

[5]杨杰军，克珠.“圆的周长”教学设计[J].中国电化教育，2000，（8）.

[6]盛男.《圆的周长》教学设计[J].中国校外教育，2014，（10）.

（作者单位：浙江省绍兴市上虞区实验小学）