基于层次分析法及多因数加权平均法的项目选址评价

（广西柳州钢铁集团有限公司，广西 柳州 545002）

1 前言

系统评价的目的是为了估计系统的技术能力、工作性能和系统利用率等指标。系统的评价度量了系统当前的性能，并为进一步改善未来的系统提供依据，同时系统评价是系统决策的主要依据。影响系统好坏的因素很多，有定性和定量的因素结合，有技术、艺术和观念的因素交叉等，因此如何评价一个系统及研究系统的科学评价方法，对促进系统的建设有十分重要的意义。评价系统时，评价指标体系的建立和评价方法的选用非常关键[1]。本文主要介绍了层次分析法和多因素加权平均法在选址方案中的应用，确保选址的合理性。

2 评价方法介绍

2.1 层次分析法

层次分析法是美国运筹学家T.L.萨迪（T.L.saty）于1973年提出来的，适用于结构复杂、决策准则多且不易量化的决策方法。该方法将许多复杂、模糊不清的关系转化为定量分析的问题，具有实用性、完整性等优点，大大提高了决策的有效性、可靠性和可行性。其主要步骤为：（1）建立层次结构模型；（2）构造判断矩阵；（3）层次单排序及其一致性检验；（4）层次总排序；（5）层次总排序的一致性检验。

层次分析法将对决策有影响的各项指标组织成层次结构，并赋予它们一定的优先数，利用数学方法计算各指标和方案的综合得分或优良度，以此指导决策。

在对各指标进行定量赋值时，应由专家和决策人员根据自身的经验和对项目的了解程度进行合理评价，但由于评价人员的出发点和专业层次不同，对评价标度的掌握往往存在差异，存在不满足一致性检验的情况，因此，在对各指标进行测评时，常与模糊综合评价法配合使用[2]。

2.2 多因数加权平均法

多因数加权平均法是系统评价方法中最简单、可行性最高的一种。其基本步骤是：首先确定评价指标；再由专家组分别对各指标的重要性和合理性进行打分，同时还要为各专家分配一个权重；根据专家权重及指标的重要性得分、合理性得分，分别计算指标的权重和得分；最后求得系统的综合加权平均值。该方法的权重确定依赖于专家知识，其评价结果无法摆脱主观随意性的影响[1]。

3 项目选址评价

不同项目的选址要求各不相同，在项目的选址中要充分根据项目的特点进行分析，利用层次分析法进行评价，最关键的步骤就是建立层次结构模型。层次结构模型的建立就确立了项目选址的评价指标，以及各指标间的影响关系。而判断矩阵的构造、层次单排序及其一致性检验、层次总排序以及层次总排序的一致性检验都是数学方法的计算过程。本文主要以对某企业物料输送系统的储存及中转中心选址进行评价为例对该方法进行介绍。

3.1 确定储存及中转中心选址的主要评价指标，建立层次结构模型

应用层次分析法分析决策问题时，首先要把问题条理化、层次化，构造出一个有层次的结构模型。在这个模型下，复杂问题被分解为元素的组成部分，这些元素又按其属性及关系形成若干层次，上一层次的元素作为准则对下一层次有关元素起支配作用[3]。

储存及中转中心选址层次结构模型包括目标层、准则层、基本层。目标层即选址评价，准则层包含：运输条件、政策因素、自然条件、经济因素、其它因素。评价指标层次结构模型如图1所示。

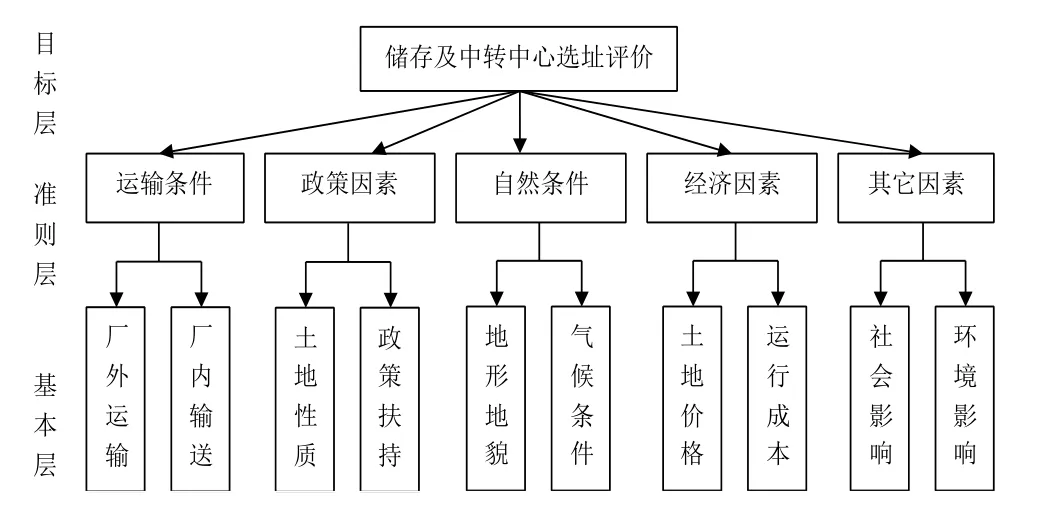
图1 评价指标层次结构模型

3.2 构造判断矩阵，确定权重系数

对选取的各评价指标，采用专家调查法，按照其在储存及中转中心选址决策中的影响程度及在评价体系中的作用，对其进行两两比较并构建判断矩阵。比较标准采用1-9标度法，详见表1，准则层重要程度综合评价表见表2。

表1 1-9标度法判断等级划分

表2 准则层重要程度综合评价表

对判断矩阵进行归一化处理，求出每一行的几何平均数和权重系数。

第一步：计算判断矩阵每一行元素的乘积mi：

第二步：计算mi的n次方根，即几何平均数：

则w=[w1,w2，…，wn]T即为所求特征向量。

该储存及中转中心选址决策中判断矩阵及每一行的几何平均数、权重系数见表3。

表3 判断矩阵、几何平均数和权重系数

3.3 一致性检验

建立判断矩阵后，必须对其进行一致性检验，检验该判断矩阵是否具有满意的一致性。方法如下：

计算特征向量的最大特征根λmax：

其中：CW=C×w，C为判断矩阵。

计算一致性指标CI：

λmax为判断矩阵的最大特征值，计算一致性比率CR。

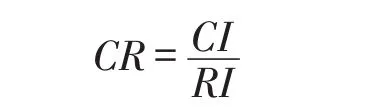
其中：RI为平均随机一致性指标，见表4。

表4 平均随机一致性指标值

当CR＜0.1时，认为判断矩阵具有满意的一致性；否则，需要重新调整判断矩阵中的元素取值，直到判断矩阵具有满意的一致性为止。

由表3可得：

查表得知n=5时，RI=1.12，所以：

一致性检验通过，因此认为该判断矩阵具有满意的一致性。

3.4 基本层分析

同以上方法，分别求得该储存及中转中心选址决策模型中基本层的权重系数，见表5-表9，经一致性检验，均具有可接受的一致性。

表5 运输条件基本层判断矩阵、几何平均数和权重系数

表6 政策因素基本层判断矩阵、几何平均数和权重系数

表7 自然条件基本层判断矩阵、几何平均数和权重系数

表8 经济因素基本层判断矩阵、几何平均数和权重系数

表9 其它因素基本层判断矩阵、几何平均数和权重系数

3.5 层次总排序，确定基本层对目标层的总权重

以上步骤已确定了准则层对目标层的权重，基本层对准则层的权重，根据以上数据进行层次总排序，可以计算该储存及中转中心选址决策模型中基本层对目标层的总权重，见表10。

表10 层次总排序

3.6 采用多因素加权综合评价法进行方案总评价

组织有关专家对各指标进行逐一评价，根据专家权重及打分情况计算每个指标的加权平均分值，即为各指标的最终得分。评分采用十分制，评分细则见表11。

表11 评分细则

本文不详细介绍各指标加权平均分值的计算过程，根据各指标最终得分及各指标总排序权重，求得该储存及中转中心选址最终得分。方案总评价得分详见表12。

表12 方案总评价得分表

根据表12数据，该选址方案最终得分为8.213 7，根据评分细则，认为该选址方案对项目的建设和运行有利。

以上步骤介绍了对单一选址区域的评价，采用层次分析法对项目实施的各影响因素进行权重计算，再通过多因素加权平均法对选址方案进行综合评价。对于多方案的比选评价，可以采取同样的步骤得到选址方案的评分，根据综合评分情况进行选择。

4 结语

本文结合层次分析法及多因数加权平均法的优点，对某企业储存及中转中心的选址问题进行评价，层次分析法将配送中心选址方案的定性指标定量化，将各指标层次化、清晰化，各指标权重分配科学合理，结合多因素加权平均对项目选址进行最终评价和比选，以达到降低成本、加快生产系统反应速度、促进系统中各环节的协调配合，得出最优选址方案。由以上选址评价案例可知，基于层次分析法和多因数加权平均法的项目选址评价法具有较强的操作性和可实施性。