基于GARCH-VaR模型的外汇风险度量方法的统计比较

申 利

（陕西理工大学 经济与法学学院，陕西 汉中 723001）

0 引言

近年来，西方国家贸易保护主义有所抬头，对大部分业务在国外的进出口企业来说会遇到不少风险，其中面临的外汇风险尤为突出。外汇风险是由于外汇交易而产生的风险，是因为有一部分外汇头寸处于暴露状态，但风险暴露并没有对外汇风险带来的损失程度给予明确数量表示，而外汇风险程度是不确定的。因为企业只有在对外汇风险有充分的认识后才能制定最为恰当的风险管理措施，外汇风险计量也就成为企业外汇风险管理体系中不可或缺的一环。周爱民（2017）[1]提出偏t分布的GARCH-时变Copula-CoVaR模型，以测度内地和香港两地股市和汇市四个市场两两间的风险溢出效应。研究表明,相关的GARCH-VaR模型可以测度金融市场间的风险溢出效应。邹正方和李建成（2010）[2]构建参数法下的GARCH模型对外汇市场存在的风险进行计量分析,并运用VaR方法进一步计算外汇资产的风险补偿金,可以实现预测和控制外汇风险的目的。刘晓峰和曹华（2012）[3]利用加入宏观信息的GARCH模型为基础的VaR方法对外汇风险进行了度量，发现加入宏观信息可以增加估计的信息量，从而提高VaR的度量效果。叶伟和杨招军（2015）[4]提出用VaR度量不同币种外汇资产组合，为提高VaR计算的精确性，在计算过程中引入Copula函数，结论表明随着美元资产比重的增加，外汇储备的风险值逐渐减小。王丽君（2016）[5]基于VaR风险度量理论，提出AFIMA-FIGARCH模型，研究外汇市场的波动率和收益率变化。研究发现，把FIGARCH引入到汇率市场的VaR风险度量中，更能有效地实现对外汇市场的风险度量。本文在分析比较经典的方差-协方差法、历史模拟法和蒙特卡罗法计算VaR的基础上，构建基于GARCH-VaR模型，测度人民币/美元的外汇风险。

1 VaR风险度量与计算

作为风险度量工具的VaR，由于具有对风险测度的科学、实用、准确和综合的特点，并且能与一系列检验方法相结合，迅速在风险管理、绩效评估、金融监管等领域得到广泛应用[6]。其表达式为：

式（1）中，a为置信水平，Δp为给定损失水平，VaR为置信水平a下的风险价值。

VaR概念存在两个参数：持有期Δt和置信水平a，给定这两个参数后才能够进行VaR的计算。不过VaR计算风险价值时有相对风险价值和绝对风险价值之分，本文主要分析集中在绝对风险价值，设V0为某一投资组合期初的投资额，设投资期收益率为R，则期末该组合价值为V=V(1+R)。记投资期的期望收益率为μ，即μ=E(R)。设在置信度α下的投资组合最低收益率为R*，在已知期望收益率和资产或资产组合未来收益率的概率分布密度函数f(R)的情况下，置信度α对应的最小收益率R*可通过式（2）或式（3）求出：

VaR本质上是α和f(R)的函数，在给定α的情况下，概率密度函数f(R)的确定就成为求解VaR的关键。针对概率密度的不同假设和估计，形成结构不同的VaR估计模型，具体VaR的计算总体上分为参数法和非参数法两类。

（1）参数法

方差-协方差方法是较早的计算VaR的参数方法。给定资产组合的收益率R，满足均值为μ、标准方差为σ的正态分布，也就是收益率R～N(μΔt，σ2Δt)，因此有 (R-μΔ，在置信水平α下，可用计算出最小收益率，其中za为分位数，进而有：

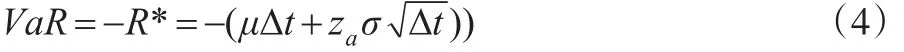
若当资产组合为多种资产时，需考虑组合的相关系数及协方差，由式（4）可知，使用方差-协方差方法计算VaR，需要处理波动率σ和分位数za两个参数。对于波动率参数σ估计，可采用历史数据的标准差进行处理；对收益率分布函数，由于实际的汇率时间序列具有尖峰、厚尾等特征，通常考虑t分布、广义误差分布（GED）等特殊的分布函数。

参数法通过假定资产收益率满足给定的分布，通过分布函数的选择来描述收益的尖峰、厚尾特征，不仅使VaR的计算变得简单，而且还能提高拟合效果。目前是应用最为广泛的计算VaR的方法。但是，参数法也存在以下不足：一是通过历史数据计算VaR，无法对特殊异常风险进行测度；二是现实中金融时间序列的波动率具有时变性，传统的波动率估算方法无法跟踪这种时变性；三是资产收益率分布假设的正确与否对模型的计算影响甚大，若假设不正确时，将会产生较大的模型误差。

（2）非参数法

非参数法主要包括历史模拟法和蒙特卡罗模拟法，对于历史模拟法，通常假定历史可重演。在假定的置信水平下，利用资产的历史过往数据推演未来的收益水平，进而计算出VaR。

历史模拟法的分析推算步骤如下：

第1步：寻求影响组合价格的所有市场因子，收集整理市场因子的历史序列数据，确定对价格影响的权重比例，并用模型设计出组合中各个工具的盯市价值，即确定资产定价公式。

第2步：根据市场因子过去n+1个日期内的时间序列，推算出n个价格实际变化值。假设市场因子未来的价格变化和以前的变化规律相同，那么利用当前市场因子的价格，就能够得到市场因子的n个未来可能的价格水平。

第3步：依据推算出的因子未来的价格序列水平，整理计算未来n个可能的价格水平，并与当前的价格进行分析对比，获得未来价格序列的可能损益值分布。

第4步：依据得到未来价格的损益分布特征和给定的置信水平，确定合理分位数，进而得到组合的风险价值，即VaR值。

尽管历史模拟法具有简单高效的特点，但也存在一定不足：首先，它假设过去的数据能代替短期的未来，完全依赖于历史数据所提供的信息，若资产价格波动过大，估计值将有很大的偏差；其次，设定所有的观测值等权重，这也与事实不符，通常近的观测值对未来的影响大；最后，该方法结果的准确性依赖于样本的充足性和可靠性，若样本容量太小或包含过多的偶然性事件，将大大影响VaR的可信度。

蒙特卡罗模拟又称随机模拟法，该方法在VaR中的应用是基于资产组合价格变化服从几何布朗运动的随机过程，即：

其中，yt满足标准的布朗运动，即(0，1)。St为资产在时刻t的价值，参数μt和σt分别代表资产价格的瞬时漂移率和波动性。

在模拟单个资产的价格变化时，先将式（5）离散化，得到：

其中，Δt=(T-t)/m，t为当前时刻，T为未来时刻，m为模拟路径的段数。εt表示服从标准正态分布的随机变量。又因为ΔSt=St+1-St，所以式（6）可表示为：

于是给定St，并计算出相应的μt和σt，通过产生随机序列εt（t=1，…，m），代入式（7），最终可得资产未来一个可能的价格ST。重复上述过程就可以得到资产未来价格的一个分布，进而得到一个可能的损益分布。只要重复的次数足够多，那么所得到的损益分布就会无限接近实际的损益分布，加上由置信度确定的分位数，就可以推算出VaR值。

2 GARCH-VaR模型的构建

在金融市场中，金融数据通常具有时变特征，这就是异方差现象。广义条件异方差自回归方程（GARCH）可以很好地刻画这种现象。实际应用最为广泛是GARCH（1，1）模型，其方程组结构如式（8）至式（10）所示：

其中，式（8）为均值方程，式（10）为方差方程，α为方差方程的一阶滞后项估计系数，β为方差方程的方差一阶滞后项估计系数，在式（9）中通常假设εt与σt不相关，且满足标准正态分布。通常情况下金融资产价格波动规律具有一定的随机，且呈现非对称特征，TARCH模型和EGARCH模型可以有效解决这种非对称性问题，这两种非对称模型具有不少相似性，不同体现在方差方程上。

TARCH模型的条件方差方程为：

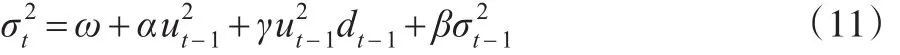
式（11）中，若ut＜0时，有dt=1；否则，有dt=0。上升(ut＞0)和下降(ut＜0)对条件方差方程的冲击是不同的：上升的时候，有一个α单位的冲击影响；下降的时候，则有一个α+γ单位的冲击影响。若γ≠0，则信息存在非对称效应；若γ＞0，存在非对称加大杠杆效应，冲击会加大波动；若γ＜0，非对称杠杆效应存在使得波动幅度减小。

EGARCH模型的条件方差方程结构为：

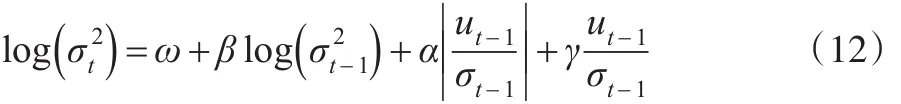
式（12）中，左边是t时刻方差的对数形式，说明杠杆影响呈现指数特征变化。若γ≠0，说明冲击响应的影响存在着非对称性特征；若γ＜0时，非对称杠杆作用的冲击更加明显。

通过GARCH模型的方差方程计算出时变的方差，利用式（5）得出时变的VaR。上面均假设εt满足标准正态分布，对于数据的尖峰、厚尾分布特征，可用t分布和GED分布来刻画。

3 实证分析

3.1 经典VaR外汇风险计量检验

本文数据选取自2013年10月10日至2017年11月20日之间的836个人民币/美元汇率数据作为总体实证样本，为了避免数据之间的相关性，先对数据作一阶对数差分处理。

3.1.1 方差-协方差法

计算人民币/美元的几何收益率的均值和标准差，密度函数选择正态分布和t分布，对于正态分布，分位数可以查表获得。对于t分布，采用矩估计法估计t分布的自由度，查询t分布表及插值法计算出分位数。两种分布在不同置信度下的分位数如表1所示。

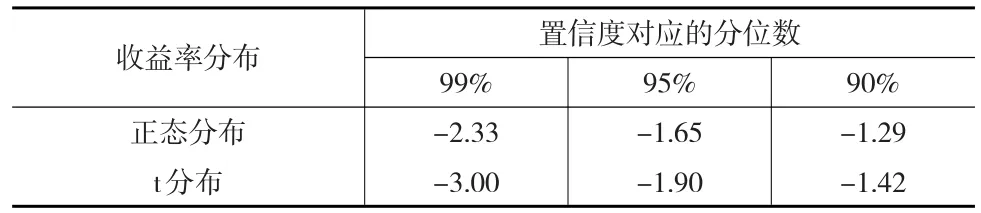
表1 两种分布在不同置信度下的分位数

由VaR=-μ-zaσ即可得到对数收益率的VaR值，如表2所示。汇率波动下界如表3所示。

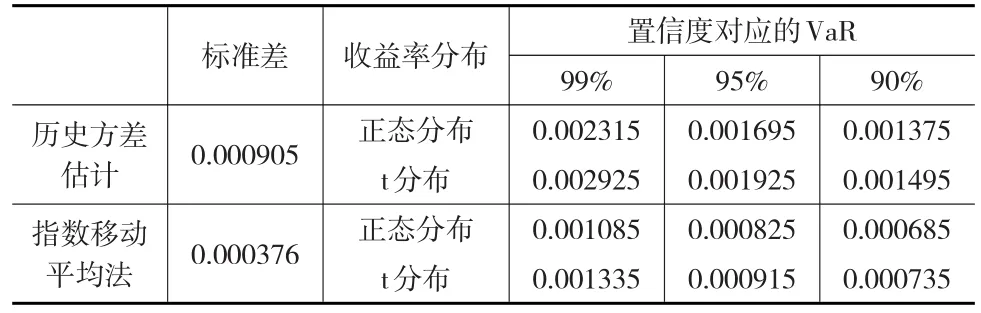
表2 方差法计算的VaR值

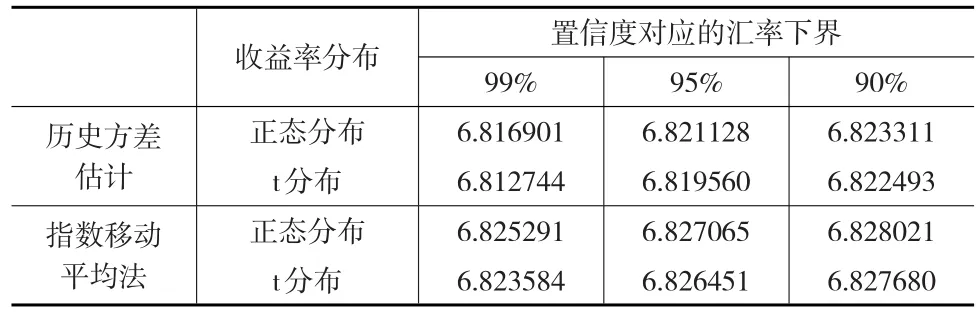
表3 方差法计算的汇率波动下界

3.1.2 历史模拟法

首先汇率对数收益率序列进行序列排序，确定分位数的具体位置，推算出不同位置的分位数R*，得到最低收益率。分别在99%、95%、90%的置信度下，计算对应的收益率，并由相应的VaR=-R*可得到各置信度下对应的VaR，同时计算出汇率波动的下界，如表4所示。

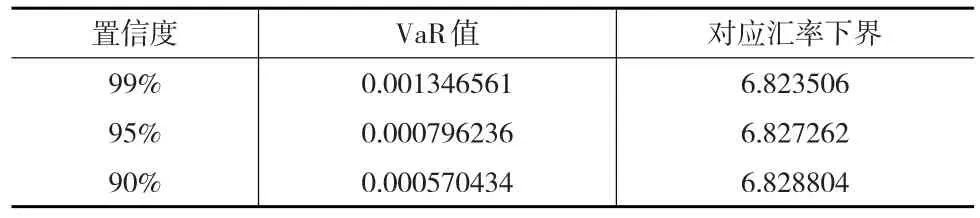
表4 历史模拟法计算的VaR值及对应汇率下界

3.1.3 蒙特卡洛模拟法

根据上文的分析，文中采用布朗运动的随机模型来描述汇率收益率的变化规律，随机方程的表达式为：

其中，ε～N(0，1)。通过人民币汇率的收益率数据计算得到μ和σ值。此外，选取样本最后一天的人民币汇率收益率为原始值，然后产生标准正态分布的伪随机数ε，代入式（13）可得汇率收益率的一个可能值。不断重复这一过程N次，就可以得到N个对数收益率数据。利用这N个数据进一步推算对数收益率分布，同时依据假定的置信水平，计算相应的收益率VaR值，进而得到最后样本日期的汇率波动的下界，如表5所示。

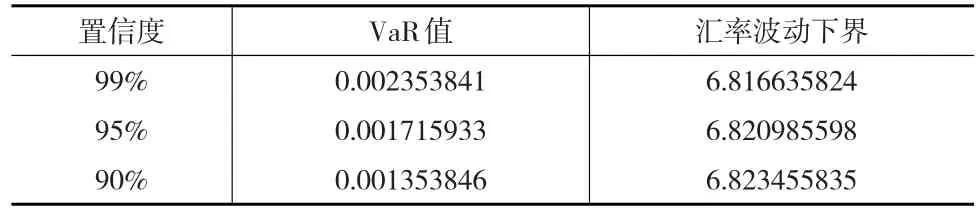
表5 蒙特卡罗模拟法计算的VaR值及汇率下界

3.2GARCH族动态VaR外汇风险计量分析

此处数据选择与3.1相同，只是将总体样本数据分为两部分。其中，2015年7月22日至2017年11月1日之间的542个数据为实证样本，另一部分作为验证样本。对两组数据分别进行一阶对数差分处理，目的是避免数据序列的相关性。

3.2.1 数据异方差检验

在应用GARCH族模型之前，需要对检验数据进行异方差检验。通过检验发现，数据序列呈现明显的时变特征，可以初步判断存在条件异方差。进一步对残差序列进行ARCH-LM检验，LM检验的相伴概率为0.000002，远远小于0.05的显著性水平，进一步确认数据序列存在异方差，同时也说明用GARCH族模型进行分析是适合的。

3.2.2 GARCH-VaR外汇风险计量

实际的分析中，GARCH（1,1）模型由于结构简单、易处理，应用也最为广泛。本文采用GARCH（1,1）模型，首先对于实证样本数据，采用极大似然估计法GARCH族模型进行参数估计，模型中残差分别满足于正态分布、t分布及GED三种分布，分析结果如表6至表8所示。

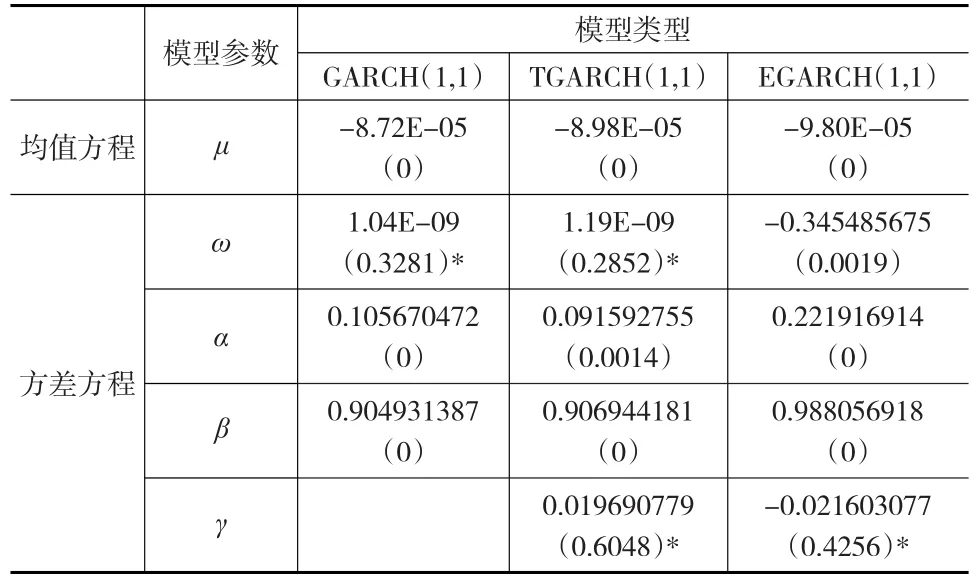
表6 正态分布下的GARCH估计结果

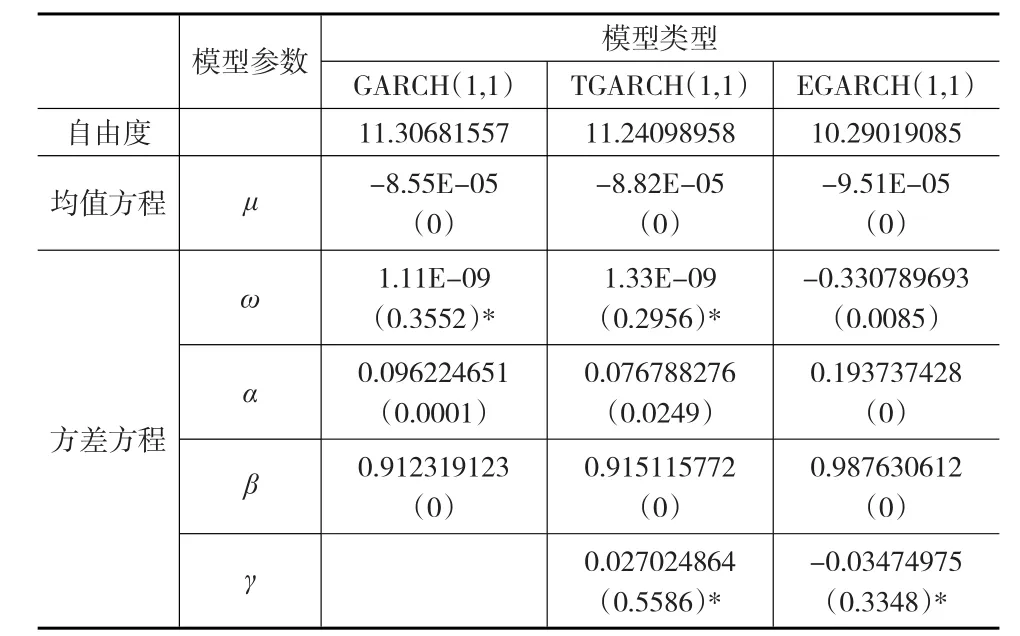
表7 t分布下的GARCH估计结果

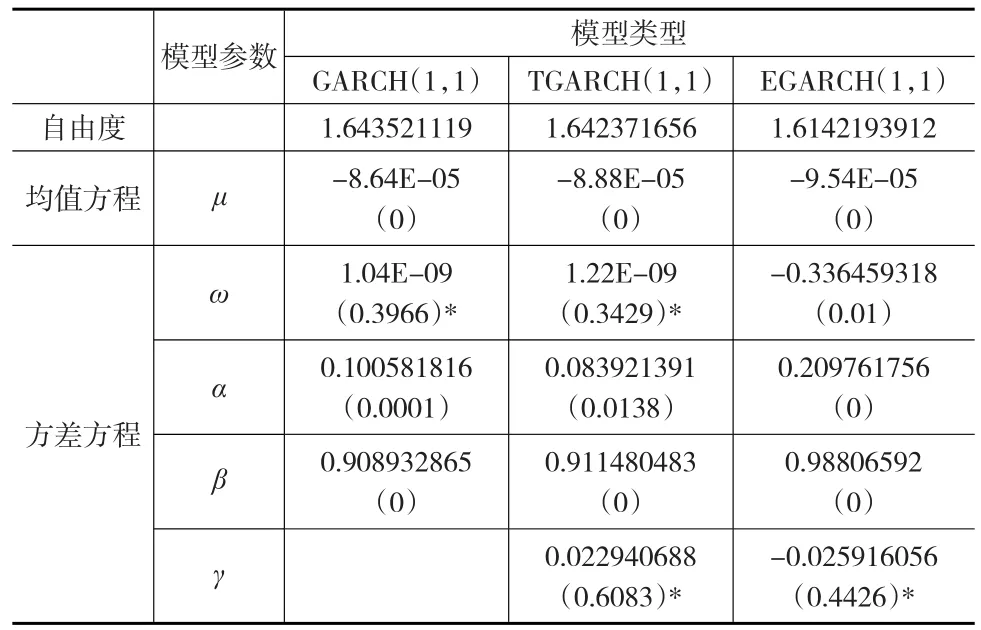
表8 GED分布下的GARCH估计结果

从表6至表8的估计结果来看，不管分布函数如何假定，对于TGARCH和EGARCH两个非对称性模型，其参数γ均不显著，这也表明汇率数据序列条件异方差不存在显著的杠杆效应。GARCH模型估计可以替代TGARCH和EGARCH估计，三者估计结果没有明显的区别，而GARCH模型更为简洁。因此可选择最优的GARCH（1,1）估计VaR值。

另外，对于GARCH（1,1）模型，残差序列不管在何种分布情形下，其模型的估计值在1%置信水平下均显著。规律具有以下特征：GARCH（1,1）方差方程的冲击响应系数α均为正，说明汇率序列数据具有波动集群性特征。不过α小于等于0.2，不少文献作了经验性研究，资本市场中的日收益率数据，通常反映系数满足这一要求，表明数据的波动引起金融市场的反应并不强烈;估计系数α+β大于1，说明波动存在聚集性的同时，也具有一定的持久性特征，条件方差对冲击响应将会不断的强化，产生长久记忆。即汇率序列存在持续性波动，短期内难以逼近均值，当前讯息的重要性得到加强；μ的估计明显小于0，反映汇率序列数据的均衡收益为负，市场风险相对较大。

4 结论

本文应用方差-协方差法、历史模拟法、蒙特卡洛法等计算VaR的方法对人民币/美元汇率风险进行计量研究，结果表明这三种方法计算的VaR均能很好地覆盖人民币/美元的外汇风险。随后，利用实证样本构建GARCH（1,1）模型，发现汇率收益率数据的条件异方差不存在显著的杠杆效应。并进一步研究了可以刻画汇率异方差特性的GARCH（1,1）模型，在此基础上推算动态VaR，分析发现考虑条件异方差GARCH（1,1）的动态VaR模型不仅可以测度当前的外汇风险，也能对未来一段时间内外汇风险加以测度和管理。理论和实证研究结果均表明VaR方法是一种有效的外汇风险度量方法。