制造业泰尔熵指数及其对全要素生产率TFP的影响研究

吴敏洁，徐常萍，唐 磊

（1.东南大学 经济管理学院，南京 211102；2.南京信息工程大学 商学院，南京 210044）

0 引言

21世纪初，Yong（2000）[1]提出了著名的“地方保护主义上升，导致改革开放期间中国国内市场分散化”的观点，引起了国内学者的关注，白重恩等（2004）[2]关于同时期产业集聚度上升的发现反驳了Young。尽管在产业部门集聚水平增强还是减弱问题上存在分歧，但双方就地方保护主义的存在，以及由此引发的效率损失给予了肯定。此后，陆续有学者对中国制造业集聚程度与变动趋势进行了研究，得到的结论有：（1）从20世纪末到21世纪初，制造业集聚水平不断提升，一些学者发现2004集聚拐点出现，另有学者认为拐点持续时期较长——在2003—2008年期间；（2）部分产业呈现由东部向中部和西部扩散态势；（3）与发达国家相比，中国制造业集聚水平较低，集聚效应有待增强[3-6]。另有一些文献论证了集聚对生产率的影响，Ciccone和Hall（1996）[7]通过集聚的生产函数模型构建，检验了美国和欧洲产业集聚对劳动生产率的正向促进作用，指出在密集地区，集聚的正向效应大于并抵消了拥挤效应。范剑勇（2007）[8]证实了集聚对中国非农产业劳动生产率的促进作用。然而，集聚超过一定程度，会导致竞争恶化，成本上升，产生集聚不经济[9]。研究发现，我国部分劳动密集型制造业出现过度集聚，阻碍了生产率提高[10,11]。随着环境问题的日益突出，学者们逐渐关注集聚对包含能源和污染排放因素的全要素生产率的影响，但研究结论存在较大分歧[12，13]。事实上，行业的异质性造成不同制造行业的集聚程度，变化趋势和集聚影响差异较大，本文从制造业行业的异质性特征入手，考察集聚对制造业全要素生产率的影响，为政府部门制定产业集聚政策提供参考。

1 模型的构建

1.1 理论模型

Combes（2008）[14]构建了基于产业s某厂商i的Cob-Douglas实物量值生产函数模型：

其中，Ai为希克斯中性技术进步，li表示劳动力，μi是劳动力的效率水平。ki为劳动力以外的其他投入品。设yir为该厂商产品销售到区域r的产品数量，pir是扣除中间产品边际成本后销售到区域r产品的出厂价格，该厂商生产产品平均单位价值（扣除中间产品后）：

由式（1）和式（2）可得到某厂商i的Cob-Douglas货币量值生产函数模型：

全要素生产率（TFP）是厂商所有产出和所有投入之比，则有：

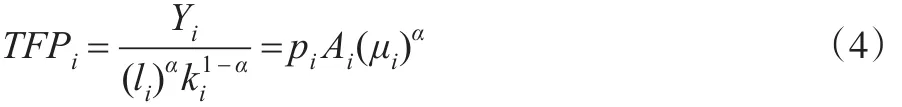
上述全要素生产率未考虑环境效率，能源是生产活动中的重要投入要素，以二氧化碳为代表的污染物排放和能源使用有着直接关系，随着环境规制的日益严格，化石类“不清洁”能源的使用会增加厂商的治污成本，造成生产性投资的挤占，抑制厂商整体产出，本文在式（1）基础上增加能源要素，得到：

式中，hi表示能源的清洁度，能源含碳量越高，清洁度hi越小。相应地，考虑环境（二氧化碳）因素的全要素生产率：

整体产业s的环境全要素生产率可以由所有厂商全要素生产率的平均值来表示：

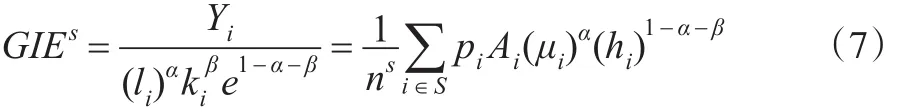
式中，ns是产业s的厂商数量。

因此，影响产业全要素生产率的因素有如下四个：（1）产业厂商技术水平Ai；（2）产业厂商出厂价格pi；（3）产业厂商劳动力效率μi；（4）产业厂商清洁能源的使用hi。

1.2 实证模型

产业的空间分布通过对四个变量的作用来影响产业全要素生产率，适度的产业集聚可以产生技术溢出，提高厂商的技术水平Ai；其次，产业厂商集中于需求地或者中间品生产供应地，可以获得较高的价格水平pi；再者，集聚产生的劳动力“蓄水池”效应，可以提供更多熟练劳动力，劳动力效率μi相应较高；最后，相对于散点分布，产业集聚可以形成污染治理的规模效应，便于清洁能源的统一推广使用。另一方面，集聚区过度拥挤——竞争加剧，劳动力、土地成本攀升，将抑制价格水平pi。对污染密集产业来说，集聚地宽松的环境规制政策，往往导致能源和环境资源的滥用，形成“污染避难所”。

据此，本文提出：

假设1:产业集聚会对制造业全要素生产率产生影响，影响大小和方向不定；

假设2：不同产业对技术溢出、劳动力效率、环境红利和拥挤成本的敏感度不同，集聚对制造业不同产业的影响存在差异。

理论模型（7）可以转换为全要素生产率与集聚水平的回归模型，增加控制变量和误差项后，t时期产业S的集聚对全要素生产率的影响的基础模型如下：

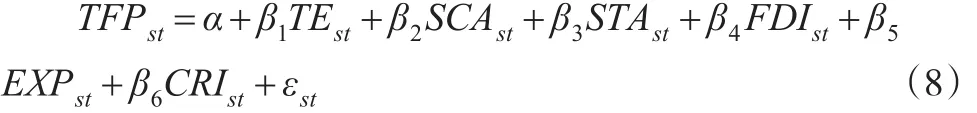
其中，下标S表示产业，t表示时间，TFP表示制造业全要素生产率，TE代表产业集聚水平，控制变量包括：（1）厂商规模（SCA）。除了集聚带来的产业层面规模经济，还有来自企业层面的规模经济，厂商平均规模越大，来自企业层面的规模效应越强。规模经济是生产率提升的重要源泉，预期厂商规模正向影响全要素生产率。以单位制造业产值来表示。（2）国有经济（STA）。国有经济由于其特殊的产权障碍，一定程度影响了资源配置。预期负向影响全要素生产率。（3）外商投资（FDI）。外商投资是国内企业获得技术溢出的重要来源，预期其正向影响全要素生产率，用外商资本占比表示。（4）出口（EXP）出口是获得技术溢出的有一途径，另外，出口带来外部需求增加，有助于价格上升，是促进全要素生产率的又一动力，预期正向影响全要素生产率，以出口交货值与产值比表示。（5）经济危机（CRI）。改革开放使中国迅速融入全球经济，进入21世纪，全球经历了两次接踵而至的经济危机，给中国带来了一定冲击，因此，引入虚拟变量，并设2008年、2009年、2010年和2011年为1，其余年份为0。考虑到经济危机摧毁的一般是技术落后、生产率低下、缺乏竞争优势的企业，预期其对制造业生产率产生正向影响。ε表示误差项。

2 测量方法

本文数据来源于2002—2017年的《中国统计年鉴》《中国工业统计年鉴》《中国能源统计年鉴》以及中国30个省/直辖市（西藏除外）的统计年鉴，统计口径为“规模以上工业企业”。2001—2016年间，我国《国民经济行业分类代码》经历了2次修改，为了保证行业一致，本文对修改中涉及的“橡胶制品业”和“塑料制品业”合并为“橡胶和塑料制品业”，汽车制造业和铁路运输设备制造业合并为“交通运输设备制造业”，最终得到了27个两位数制造业行业的相关数据。

2.1 集聚水平的测量方法

产业的空间集中度测量方法有基尼系数、艾萨德指数、熵指数、EG指数等，考虑到数据的可获得性，本文采用熵指数法，它具有特殊的可分解性，可以将产业集聚分解为不同经济圈之间的集聚变动和经济圈内的集聚变动。

假设s=1，…，S表示制造业产业部门，h=1，…，H表示省份，考察集中水平时需要对某一项目进行评估，即s产业部门h省份（直辖市）的某项目水平，本文选用产值代表。为部门s的总体产值。为h省份（直辖市）的总体产值。是制造业所有产业部门所有省份（直辖市）的总体产值。可得到s产业的泰尔熵指数如下：

本文将泰尔熵指数进一步分解，可得到产业在经济圈之间和经济圈内的空间集中度，见式（10）至式（12）:

经济圈内部的集聚度（TEs

w）见式（12），是对各经济圈内产业分布不均衡水平的加权累加：

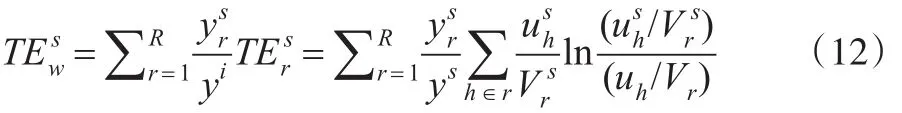
2.2 全要素生产率的测量方法

本文考察的全要素生产率指标，包含期望产出（产值）、非期望产出（二氧化碳排放）、资本、劳动和能源要素投入量五个方面，综合反映了经济与资源环境效率，采用SBM方向性距离函数[15]进行测算。该方法克服了传统距离函数无法考虑非期望产出的缺陷，可以测度给定方向投入和环境技术结构下，期望产出扩大和非期望产出缩减的可能性大小。

将K个制造业细分产业看作不同决策单元，构造生产技术前沿面，假设每个产业使用N种投入x=x1，…，xN∈，生产出M种期望产出y=y1，…，yM∈，同时排放I种非期望（“坏”）产出b=b1，…，bI∈，每一时期t=1，…，T，第K个产业的投入产出值为。运用数据包络分析，可以得到环境技术模型：

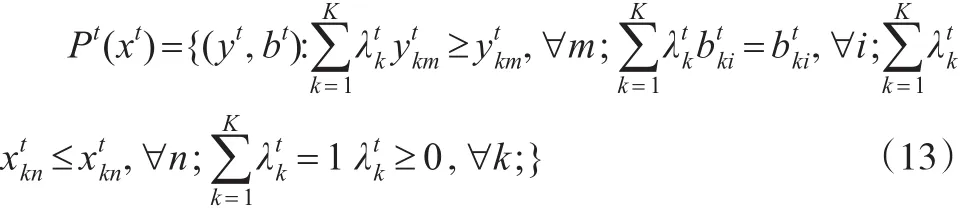
表示每个横截面决策单元观测值的权重。在式（4）基础上构建基于规模报酬可变的SBM方向性距离函数

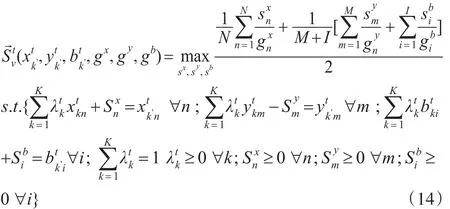
3 制造业泰尔熵指数度量结果

本文根据OECD制造业技术密集程度和劳动密集程度划分标准将27个制造业细分产业分为：技术密集型制造业（9个）、低技术劳动密集型制造业（10个）和低技术资本密集型制造业（8个）。根据上文集聚测量方法，计算得到2001—2016年二位数制造业细分产业的泰尔熵指数和主要集聚区域。集聚区域依据国务院发展研究中心（2005）发布的四大板块（东部、东北、中部和西部）、八大经济经济圈划分方法，测算结果见下页表1。

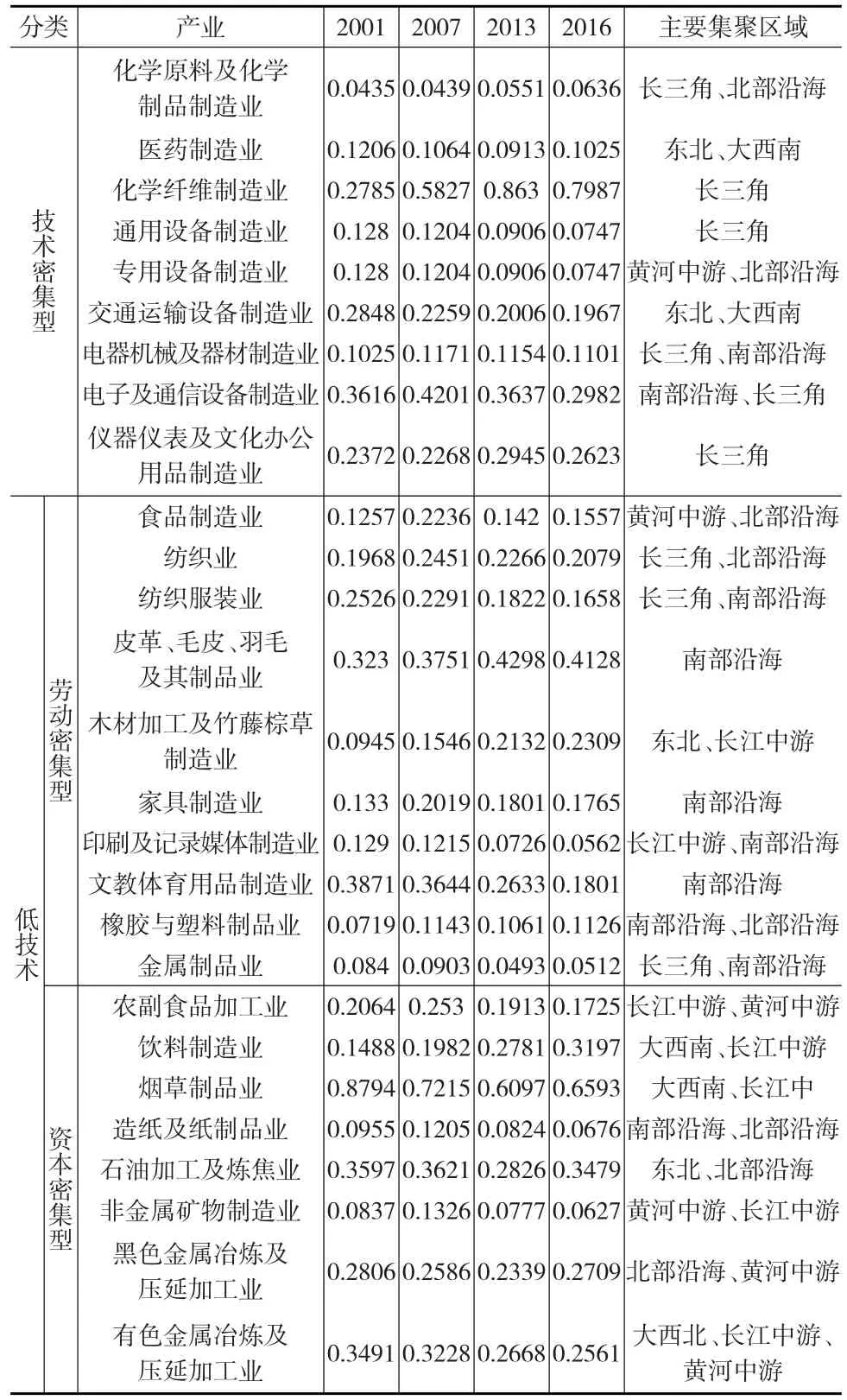
表1 2001—2016年制造业各产业泰尔熵

从集聚程度来看，我国多数技术密集型制造业集聚水平低，其中，化学原料及化学制品制造业泰尔熵指数平均值各行业最低。要素特征决定了技术密集型产业具有较高的规模经济和范围经济，受拥挤成本和运输成本影响的程度低于其他产业，地方保护主义壁垒或成为阻碍技术密集型产业集聚的原因。化学原料及化学制品、交通运输设备、通用设备、医药制造等技术密集型产业规模庞大，对地方收入影响显著，由于某种偏好性质引起的产业部门的集聚与分散，宏观上会产生效率损失，抑制经济发展。

从产业的专业化集聚区域来看，技术密集型制造业主要集中于长三角经济圈，装备制造业、化学工业等成为长三角优势产业。南部沿海在电子及通信设备制造业表现出绝对的专业化优势。此外，一些低技术劳动密集型产业也主要集中于南部沿海经济圈，加工贸易导引下，皮革、服装、玩具产业在地方经济中占有重要比重。低技术资本密集型产业则更多集中在长江中游、黄河中游、大西南等中、西部板块，以国有经济和污染密集为特征。

从集聚演变趋势来看，2001—2016年，制造业集聚整体呈现先上升后下降的态势，集聚短期变动的主要原因为制造业活动在经济圈间分布的差异，各经济圈内集聚度随时间变化相对稳定。

4 实证结果

4.1 空间分布对制造业整体全要素生产率的影响

实证模型中被解释变量——全要素生产率的值在0～1间，分别在最低界限值（0）和最高界限值（1）处被截断，传统的线性面板不再适用此类回归，文章采用专门处理截断数据的Tobit面板模型。由于个体异质性充分统计量的缺失，无法对固定效应Tobit模型进行条件最大似然估计，因此，分别采用混合Tobit回归（混合OLS）和随机效应面板Tobit回归（RE）进行估计，运用stata14.0软件，结果见表2。

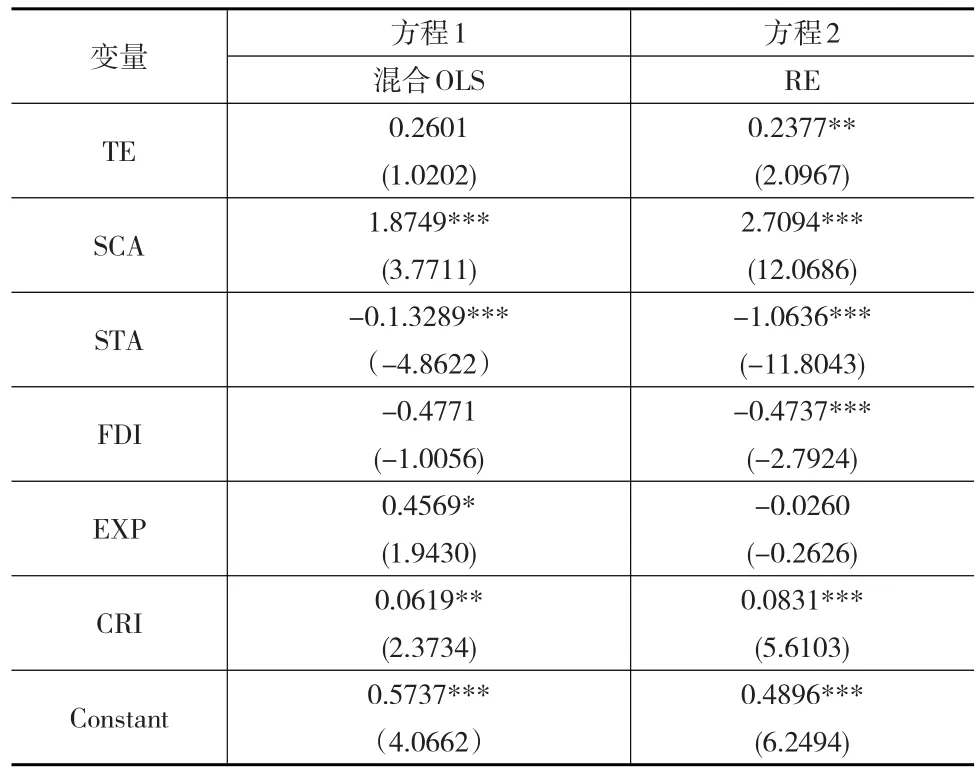
表2 制造业整体回归结果

对模型进行LR检验，结果强烈拒绝“H0:σu=0”，认为存在个体效应，故应选择随机效应面板Tobit回归检验集聚对制造业全要素生产率的影响，结果显示：（1）产业集聚促进了制造业全要素生产率的提高，且通过1%的显著性检验，假设1得证。在控制了厂商规模效应，国有经济、外商投资等因素后，制造业集聚水平每提高一个单位，全要素生产率平均增加23.77%，厂商规模同样显著促进全要素生产率的提高，相比其他因素系数最大，说明规模效应是“集聚红利”的主要来源。（2）国有经济和外商投资负向抑制造业全要素生产率，且通过1%的显著性检验。表明国有企业资源配置效率低，制约了产业效率提高。外商投资是获得发达国家技术溢出的重要途径，对全要素生产率的负向作用与预期相反，可能的解释是：随着国内外制造企业技术差距的缩小，外商投资的溢出效应减弱，一些行业对外商投资的过度依赖，阻碍了国内企业的溢出吸收和自主创新。一些外商投资以母国利益为核心，将母国淘汰的技术和污染产品转移到中国，给中国制造业可持续发展造成了损害。（3）出口负向影响制造业全要素生产率，但不显著。出口的技术溢出效应和需求扩张作用未见显著影响。我国出口产品结构不合理，初级产品、低附加值产品和污染密集型产品占有很大比重，一定程度影响了要素配置效率。（4）经济危机正向影响制造业全要素生产率，且通过显著性检验。反映了环境压力对制造业生产率改善的促进作用。

4.2 空间分布对制造业全要素生产率影响的行业差异

按前文所述分类对制造业进行分类回归，LR检验均拒绝了不存在个体效应的假设，继续选择随机效应面板Tobit模型，结果见表3。

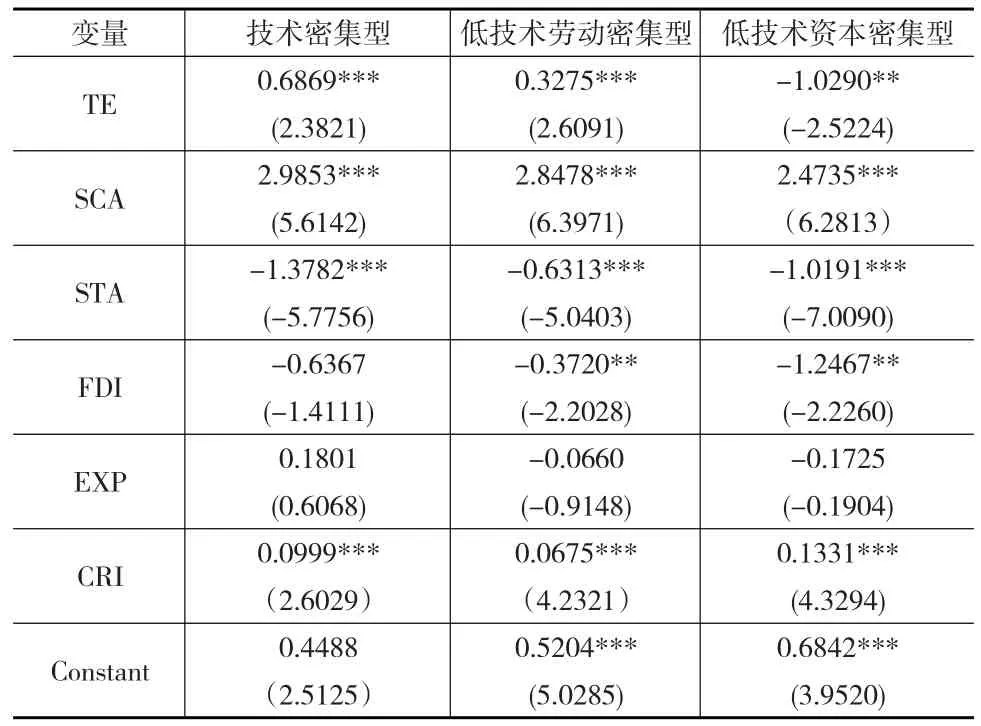
表3 制造业分类回归结果

集聚对不同制造行业全要素生产率的影响差异显著：集聚促进了技术密集型制造业和低技术劳动密集型制造业全要素生产率的提高，且通过1%显著性检验；相反，集聚显著抑制了低技术资本密集型制造业全要素生产率，假设2得证，核心解释变量的回归结果显示：（1）技术密集型产业的回归系数最大，反映集聚对技术密集型产业有更强的正向影响，知识是技术密集型产业最主要的投入要素，然而，个体间知识传播随着空间距离的增加不断衰减，集聚可以促进思想的流动，硅谷的成功也显示集聚更有利于创造尖端技术。（2）低技术资本密集型产业主要为能源强度高的污染密集型产业，集聚对低技术资本密集型产业的显著负向作用。一定程度上验证了“污染避难所”假说，即污染密集型企业倾向于建立在环保要求较低的区域。我国一些污染密集型产业主要集中在中部和西部地区,相比东部更为完善的的基础设施和劳动力人才供应市场，一些中、西部地方政府倾向通过更为宽松的环保措施吸引污染密集型企业设厂，造成能源和环境的透支，一定程度制约了环境和全要素生产率的提高。（3）低技术劳动密集型产业的集聚系数为正，说明过度拥挤并未在我国低端劳动密集型产业的集聚中占据主要效应。近来我国长三角和南部沿海的纺织服装、文教体育用品等产业已经出现向中部邻接区域的转移，加速承接区域的集聚，符合产业效率和区域发展要求。

5 结论

制造业各行业集聚水平及对生产率影响的研究结果显示，在2001—2016年间：（1）技术密集型制造业主要在东部区域集聚，并呈现强化趋势，但集聚程度较低，低技术劳动密集型制造业主要集聚在南部沿海，集聚水平在2008年后快速下降，出现向中部和西部转移态势，以污染密集为代表的低技术资本密集型制造业主要集中在中、西部板块，集聚强度呈现减弱。（2）集聚显著促进了制造业全要素生产率的提高，规模效应是“集聚红利”的主要来源。（3）由于行业异质性，集聚对技术密集型制造业全要素生产率的促进作用最强，劳动密集型产业其次，而具有污染特征的低技术资本密集型制造业集聚存在显著负向影响，印证了“污染避难所”假说。