我国海水养殖产量的波动特征及影响因素分析

陈 琦

（宁波大学 商学院，浙江宁波 315000）

1 研究方法与数据来源

0 引言

在当前渔业转型发展的关键时期，确保海水养殖生产稳定的意义重大。必须准确把握海水养殖产量的波动规律特征，以此为理论指导制定稳定生产的制度安排和政策措施，进而保障我国海水养殖业的健康发展。

有关我国海水养殖生产波动的相关研究尚不多见，其中具有代表性的有：周井娟等（2008）[1]借助Logistic曲线回归对我国海水养殖产量的波动特点和影响因素进行了定量分析，结果发现不同时期下产量波动幅度较大，近些年增长速度有放缓的趋势，影响因素分析表明水产品价格和技术进步对产量波动影响显著；孙兆明（2012）[2]通过构建海水养殖超越对数生产函数模型，对生产投入要素的产出弹性和替代弹性进行实证分析，结果表明当前我国海水养殖生产效率较低，产量的增加依然依赖于养殖面积的扩大；卢昆等（2016）[3]认为虽然我国海水养殖的规模呈现不断扩大的趋势，但养殖空间、海域开发程度、海域水质状况等均不容乐观，实际的养殖产出水平较低。总体而言，目前国内对该领域的研究较为零散，多借助时间序列模型对产量波动进行简单的长期趋势拟合分析，缺乏对短期波动特征和长期波动周期的识别，同时针对产量波动影响因素的识别研究则因应用方法的不同而存在较大差异。鉴于此，本文尝试应用H-P滤波分析法探究我国海水养殖产量的长期趋势和短周期波动特征，归纳产量波动的客观规律，同时借助逐步回归分析、状态空间模型对影响海水养殖产量波动的相关因素作具体识别，以期为海水养殖业的生产稳定提供理论支持和政策依据。

1.1 H-P滤波分析法

H-P滤波分析法的基本原理是将时间序列看作是不同频率的成分的叠加，通过分离出频率较高的成分，去掉频率较低的成分，从而去除长期趋势项，实现对短期周期波动项的度量[4]。目前，该方法已被广泛应用于宏观经济趋势[5,6]、产量波动[7,8]和价格波动[9,10]等研究领域，但尚未有应用到海水养殖生产领域的研究。H-P滤波分析方法假定时间序列Yt是由长期趋势性成分和短期波动性成分组成，对于时间序列Yt，H-P滤波就是选择一个时间估计序列Xt最小化实际值和样本点的趋势值，即：

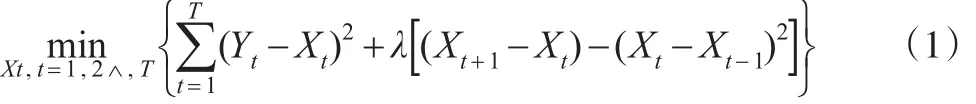
式中Yt为经对数处理后的序列值；Xt是Yt的趋势成分；λ为对趋势成分Xt波动的折算因子。令：

其中，Ct为周期成分，假设Ct与△2Xt都是独立同分布，且相互独立，则当λ=var(Ct)/var(△2Xt)时，H-P滤波达到最佳效果。综上，趋势成分Xt和周期成分Ct分别为：

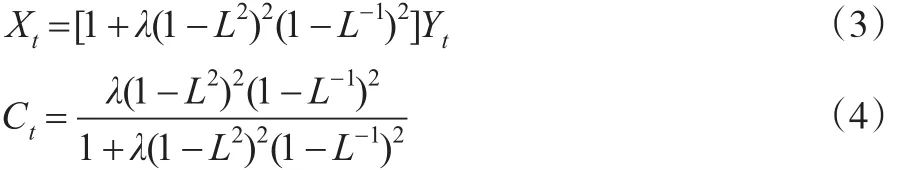
通常，当使用年度数据时，λ=100；当使用季度数据时，λ=1600；当使用月度数据时，λ=14400。由于本文的研究对象是海水养殖产量的年度数据，因此λ为100。

1.2 逐步回归分析法

影响海水养殖产量波动的因素复杂多样，本文通过建立多元回归模型，结合逐步回归分析法，识别其中的主要因素。从生产函数角度考虑，影响海水养殖产量波动的因素主要为生产要素的投入情况，具体可分为养殖面积投入、固定资本投入和劳动力投入三个主要类别。除生产要素投入外，市场因素（可用水产品价格表示）和自然风险因素（可用海水养殖受灾面积表示）同样是需要考虑的重要影响因素。基于此，选取海水养殖面积（X1）、专业劳动力（X2）、固定资本投入（X3）、水产品生产价格指数（X4）和养殖受灾面积（X5）五个影响因素作为分析对象。在对数处理的基础上，建立包含5个自变量的多元线性回归方程：

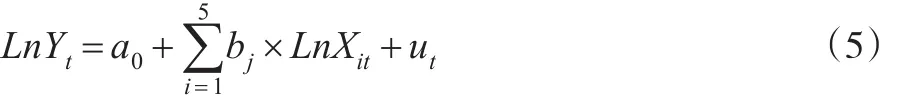
其中，a0为常数项；bj为变量Xi的系数；ut为误差。

通过最小二乘回归分析，检验模型总体回归效果。为消除多重共享性对统计检验的影响，应用逐步回归分析法，依据可决系数R2和T检验结果，从5个因素中识别出影响产量波动的主要因素。借助变量平稳性检验和协整检验进一步判断影响因素与产量之间的长期均衡关系。

1.3 状态空间模型

在一般的回归模型中，各变量的参数是固定的，用以反映变量之间稳定的影响关系。但实际上，在一个经济系统中，一些经济变量的状态是不可观测的，传统的固定参数回归模型难以表现变量之间的动态影响关系。状态空间模型建立了可观测变量和系统内部状态之间的关系，通过估计各种不同的状态向量来对系统加以分析、观测，识别其中的动态影响关系。状态空间模型包括“量测方程”和“状态方程”两个部分，表示如下：

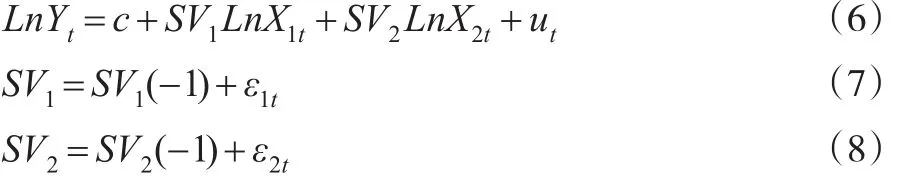
其中，量测方程式（6）反映了影响观测变量与海水养殖产量波动的关系；SV1、SV2是状态变量，反映了各个时点上海水养殖产量对各变量的弹性值，可利用Kalman滤波算法计算得到其估计值；ut、ε1t和ε2t为误差项，服从均值为0、方差为常数的正态分布。

1.4 数据来源

我国历年海水养殖产量数据主要来自《我国渔业统计40年（1949—1988）》以及《中国渔业统计年鉴》。影响因素海水养殖面积、专业劳动力、固定资本投入①由于在《中国渔业统计年鉴》中仅有渔业固定资产总投入的数据，因此参考孙兆明（2012）[2]在构建海水养殖生产函数中的处理方式，按照捕捞与养殖的产出比来估算海水养殖业的固定资产投入值。和养殖受灾面积历史数据取自《中国渔业统计年鉴》，水产品生产价格指数取自《中国统计年鉴》。

2 实证分析

2.1 总产量波动特征分析

在对原始序列进行对数处理的基础上，借助H-P滤波法，分离出1954—2016年间我国海水养殖总产量的长期演变趋势和短期波动特征。图1给出了我国海水养殖产量的H-P滤波示意图，包含了产量的实际波动曲线、长期趋势曲线和短期波动曲线。

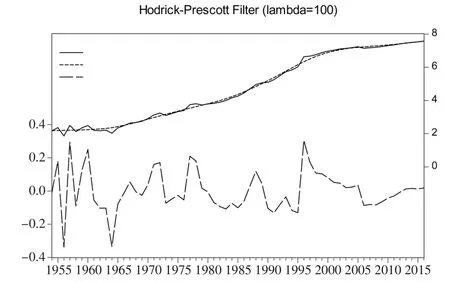
图1 我国海水养殖总产量的H-P滤波示意图

由图1的长期趋势曲线可知，在1954—1965年期间长期趋势曲线呈现出水平发展趋势，自1966年进入快速上涨阶段，并持续到2000年，随后在2001—2016年增长速度再次放缓，呈现出平滑、缓慢的上升趋势。由此可知，从长期发展趋势来看，我国海水养殖产量依次经历了“水平发展——快速上涨——缓慢上涨”三个历史阶段。

由图1的短期波动曲线可知，我国海水养殖产量在1954—1965年期间波动频繁，随后产量波动趋于稳定，特别是进入2000年以后，产量波动率基本维持在10%以内。按照“波峰－波峰”的周期划分方法，可得到海水养殖产量波动周期特征。（1）周期长度。1954—2016年，我国海水养殖产量波动经历了11个完整周期。其中，1997—2005年和2006—2014年两个周期的长度最大，达到9年。由此可见，我国海水养殖产量的周期长度实现了由短周期波动向长周期波动的转变。（2）波动高度。波动高度即波峰，反映了序列值在每个周期内的最大扩张强度。我国海水养殖产量波动高度平均值为12.29%，其中第1、2、5、9轮周期的波动高度超过了20%，这些周期基本贯穿了1954年至今的整个时期，说明长期来看我国海水养殖产量具备良好的持续扩张能力。（3）波动深度。波动深度即波谷，它反映了序列值在每个周期内的最大收缩力度。海水养殖产量的平均波动深度为-11.94%，除第1、3周期的波动深度达到-30%以外，其余周期波动深度均为-10%左右，说明我国海水养殖产量除个别年份表现出强收缩状态外，总体的收缩力度和收缩空间均较小。（4）波动幅度。波动周期反映了序列值的稳定性。我国海水养殖产量平均波幅达到24.23%，说明总体上生产的稳定性较差。但最近一轮周期波动幅度仅为0.41%，可见自1997年以来我国海水养殖生产进入稳步发展阶段，产量以平稳速度稳固增长。综上，我国海水养殖产量的波动总体上经历了波动周期长度由短到长、波动幅度由大到小的过渡。

2.2 各品种产量波动特征分析

2.2.1 鱼类产量的波动特征

由图2中的长期趋势曲线可知，我国海水养殖生产中鱼类产量总体呈现出持续增长的趋势，其中，2002年以后的长期趋势曲线走势较先前更为平缓。从短期波动曲线来看，鱼类产量在1983—2016年期间共完成了7个完整的波动周期，其中第1轮波动周期的周期长度达到11年，其余周期多为5年以下的短周期。从各周期的波动高度可以看出，各周期波动高度大致呈现递减趋势，说明鱼类产量的扩张能力在逐步减弱。对比各周期的波幅可知，除第1轮周期中波幅明显较大外，其余周期波幅基本维持在10%以内，说明我国鱼类海水养殖生产在经历了1987—1997年的波动增长后，目前已经进入了生产稳定阶段。

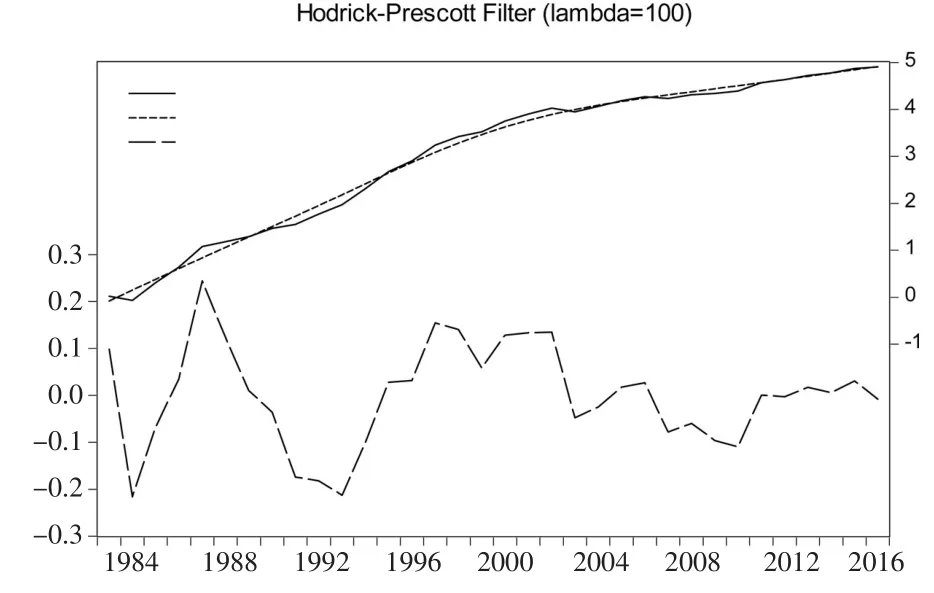
图2 鱼类产量H-P滤波示意图

2.2.2 甲壳类产量的波动特征

甲壳类产量的长期趋势曲线总体呈现出缓慢的平稳增长趋势（见图3）。依据甲壳类产量的短期波动曲线，产量在1983—2016年期间共经历了5轮完整周期，平均周期长度为4.6年，其中第2轮周期的周期长度最大。甲壳类产量各周期的波动高度呈现出显著的逐步下降趋势，到最近的第4轮周期波动高度降为负值，说明甲壳类养殖的增产能力在逐步减弱。从波幅来看，甲壳类产量的前两轮周期波幅较大，其中第2轮周期甚至达到81.38%，主要是由于该周期产量在1992—1994年期间出现较大幅度的下降，导致波动深度达到-62.35%。到最近两个波动周期，波幅则分别下降至2.04%和1.86%，生产逐步趋于稳定。

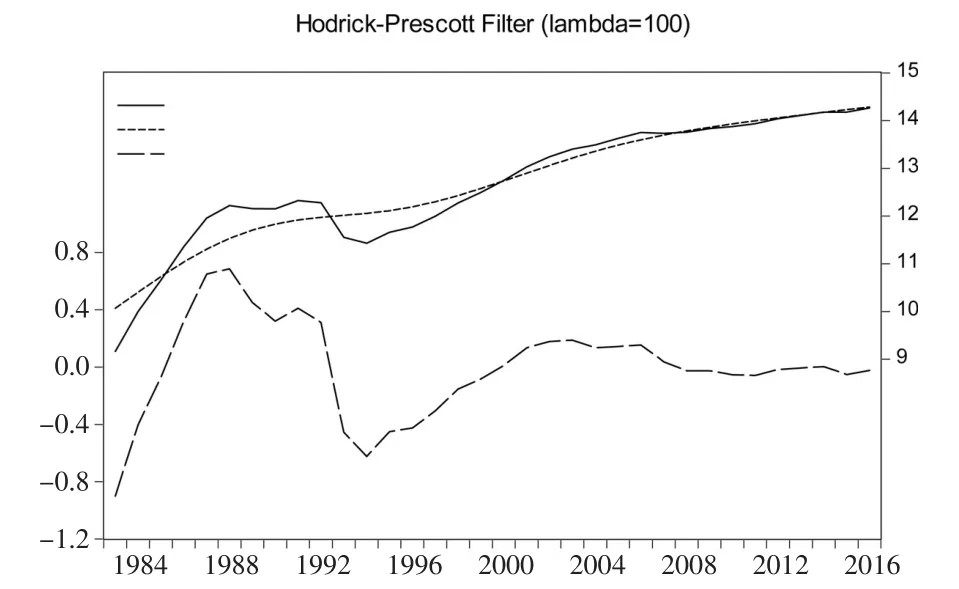
图3 甲壳类产量H-P滤波示意图

2.2.3 贝类产量的波动特征

由图4可知，贝类产量的长期趋势曲线表现出一定的阶段性特征：在1983—2001年期间呈现出持续上涨的态势，2001年以后增长趋势明显放缓，总体上表现为水平发展的趋势。从短期波动曲线来看，贝类产量在1983—2016年期间共完成3轮完整周期。对比各周期的波动高度、波动深度和波幅等特征值可知，产量在第1、2轮周期中产量波动较大，生产稳定性较差，但波动高度同样较大，说明产量扩张能力较强。进入第3轮周期后，波动高度、波动深度和波幅均大幅减小，产量趋于平稳发展。

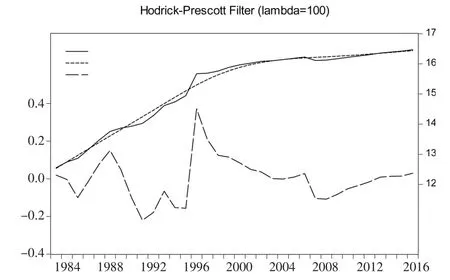
图4 贝类产业H-P滤波示意图

2.2.4 藻类产量的波动特征

我国海水养殖生产中藻类产量的长期趋势曲线总体上呈现出缓慢增长的态势（见图5）。从短期波动曲线来看，藻类产量从1983—2016年期间共完成6轮波动周期。对比各周期的波动高度、波动深度和波幅可知，与鱼类、甲壳类和贝类产量相似，藻类产量的各波动特征值同样呈现出逐步递减的趋势，生产完成了从大幅度波动到产量平稳增长的转变。但横向对比其他养殖品种来看，藻类产量在最近两个周期波动高度依然超过了5%，因此，但就近十多年而言，藻类产量的扩张能力要优于其他三类品种。

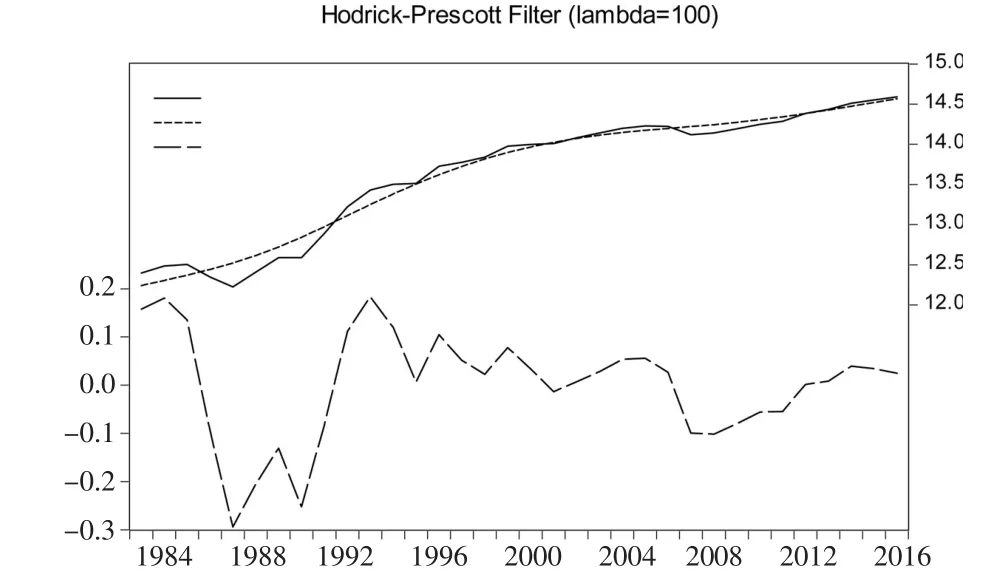
图5 藻类产量H-P滤波示意图

综上，以上四类海水养殖品种产量均经历了从波动剧烈到生产稳定的发展过程，其中甲壳类、贝类和藻类产量与海水养殖总产量相似，都大致在2007年左右进入新一轮的长周期波动阶段。从波幅来看，各养殖品种的平均波幅均超过了10%，总体上生产波动较为剧烈，比较而言鱼类的生产稳定性要明显优于其他品种。对比各品种历史周期的平均波动高度可知，甲壳类产量的平均波动高度高于其他品种，产量的历史扩张能力最大。但从短期波动曲线近5年来的末端发展趋势来看，贝类的短期波动曲线保持了向上发展的趋势，因此其近些年的增产能力相对更大。造成这种现象的原因可能是近年来鱼粉进口价格持续攀升，大幅提高了需要喂养饲料的鱼类、甲壳类等相关养殖品种的生产成本，严重制约了这些品种的生产扩大，而贝类则因无需喂养饲料，成为近年来养殖户和企业扩大生产的主要选择。

2.3 产量波动影响因素分析

2.3.1 主要影响因素的识别

考虑到数据可得性，本文选取1989—2016年5个影响因素的历史数据，在对数处理的基础上，依据公式（5）建立多元线性回归方程。借助最小二乘回归分析发现除变量X2的系数检验显著外，其余变量均不显著，说明模型存在多重共线性问题。为消除多重共线性对统计检验的影响，应用逐步回归分析法进一步识别影响海水养殖产量的主要因素。结果表明，5个影响因素中，海水养殖面积（X1）和专业劳动力（X2）两个因素表现显著，是影响产量波动的主要因素。采用ADF检验方法对序列的平稳性进行检验，检验结果表明，在5%显著水平下变量LnY、LnX1、LnX2均是不平稳序列，但这3个变量的一阶差分序列在1%的显著水平下均是平稳序列。应用Johansen检验法，通过构建VAR（p）模型，经差分变换，综合SC、AIC、LR、FPE、HQ和LogL等判断准则的检验结果，确定VAR模型的最优滞后阶数为2。在此基础上进行协整检验。检验结果发现，LnY、LnX1、LnX2序列之间存在明显的协整关系，表明海水养殖产量、海水养殖面积与专业劳动力投入之间有长期的均衡关系。

借助Eviews软件，运用Kalman滤波算法得到图6所示的影响因素弹性时变图。根据系数估计结果（见表1）可知，所有的状态空间变量均是显著的。进一步对状态空间模型的残差进行单位根检验，结果表明残差在1%显著水平下是平稳时间序列，证明模型估计的结果具有可靠性。

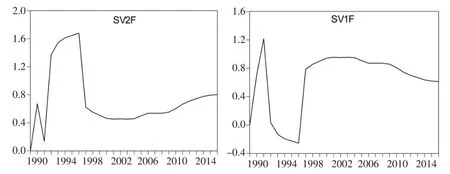
图6 海水养殖面积、专业劳动力与产量的弹性系数

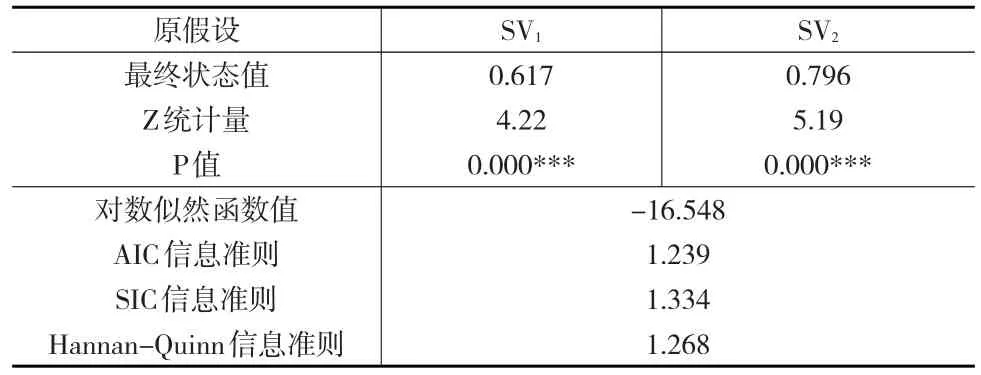
表1 状态空间模型Kalman滤波估计结果

由于Kalman滤波算法的特殊性，其前面几次取值的随机性较大，使得参数值波动幅度很大，通常被视为没有实际意义。由图6中的弹性估计值可以看出，从1997年开始，两个弹性值的波动开始趋于稳定，因此，从1997年以后的模型参数估计结果是有效的，据此对模型估计结果进行详细分析。

2.3.2 海水养殖面积对产量波动的影响

由图6可知，海水养殖面积对产量波动的弹性系数在1997—2016年期间总体上表现出波动下降的趋势，在此期间海水养殖面积每增加1%，能够带动产量增长约0.64%～0.96%。具体来看，弹性系数在1997—2003年期间出现短暂的缓慢上涨趋势，由1997年的0.78逐步上涨到2003年的0.96。而自2003年以后，弹性系数进入一个长期的下降阶段，到2016年已经降至0.61，说明产量对海水养殖面积波动的敏感程度在逐步降低，即养殖面积的增长对产量的拉动作用逐步减弱。究其原因，主要有以下三个方面：一是受自然和技术等因素的客观约束，近年来我国海水养殖只能选择向养殖条件次优或较差的海域发展。可养殖海域的空间范围是客观有限的，再加上近些年沿海城市建设、港口建设等开发活动对养殖空间的大幅挤压，导致我国近岸海水养殖空间被不断压缩。二是海水养殖品种结构的变动客观上导致了养殖面积生产弹性系数的下降。比较2003年和2016年我国海水养殖各品种的养殖面积和单产情况可以发现，贝类和藻类的养殖面积比重在增加，鱼类和甲壳类的养殖面积比重则在减小，而各养殖品种的单产情况则与养殖面积比重呈相反的变化。由于2003—2016年期间我国所增加的养殖面积更多的用于生产单产不断下降的品种，最终造成养殖面积对产量的拉动作用减弱。三是近年来我国近海污染不断加剧，严重影响海水养殖品种的存活率，造成单位海水养殖面积下的低效生产。

2.3.3 专业劳动力对产量波动的影响

由图6可知，与海水养殖面积因素相反，专业劳动力投入对产量波动的弹性系数在1997—2016年期间总体上表现为波动上升的趋势，总体而言专业劳动力每增加1%，能够带动海水养殖产量增长0.45%～0.80%。具体来看，在1997—2003年期间，弹性系数呈现出短暂的缓慢下降趋势，由0.62缓慢下降到0.45，此后进入长期的波动上涨阶段，并于2016年上涨至0.80。弹性系数的波动上涨表明专业劳动力投入对产量波动的影响作用不断加大。究其原因，一方面是随着我国“以养为主”的渔业发展方针的确立和渔民转产转业政策的不断推广，海水养殖渔户在优质种苗获得、养殖设施改善和养殖技术普及等多个层面得到了更加强有力的支持，其受教育水平和专业技术能力得以不断提高，进而推动了养殖渔户生产效率的提升。另一方面，近年来我国海水养殖产业化发展进程不断加快，进一步提高了劳动力投入的规模经济效益。1997年国务院转批农业部《关于进一步加快渔业发展的意见》中提出，在家庭联产承包责任制基础上积极推进渔业股份合作制，以加快渔业产业化发展。在该政策背景下，各地区政府通过实施优惠政策，引导地方养殖渔户在结合本地自然禀赋优势的基础上，生产同类水产品以形成大面积的单品种养殖基地，推动了海水养殖业的规模经济生产，从而使专业劳动力的投入变得更有效率。

综上，对比1997—2016年海水养殖面积和专业劳动力投入两个因素的弹性系数值可知，在1997—2011年期间海水养殖面积弹性系数值始终大于专业劳动力的弹性系数值，因此，就长期而言，产量对海水养殖面积变动的敏感度相对更大。但随着时间的推移，两个因素的弹性值差距在不断缩小，并于2012年专业劳动力的弹性值首次超过了养殖面积，成为对产量波动影响最大的因素。

3 结论

H-P滤波分析表明，我国海水养殖总产量在1955—2016年期间共完成了11轮波动周期，总体而言经历了周期长度由短到长、波动幅度由大到小的过渡。自2005年以来，海水养殖产量波动进入了长周期的平缓增长阶段，生产已逐步趋于稳定。分析1983—2016年期间鱼类、甲壳类、贝类和藻类等不同品种的产量波动特征表明，4类海水养殖品种产量均经历了从波动剧烈到生产稳定的发展过程，比较而言鱼类的生产稳定性要明显优于其他品种，而甲壳类产量的历史扩张能力最大。但单就近5年各品种的短期波动曲线发展趋势来看，贝类等低值品种的增产能力要更高，表明当前中国海水养殖产量的增长仍然主要依赖于相对低值品种的生产扩大。

逐步回归分析结果表明，海水养殖面积和专业劳动力投入是影响产量波动的主要因素。在此基础上，借助状态空间模型进一步对影响因素与产量变动之间的关系进行动态分析，结果表明，长期而言海水养殖产量对养殖面积变动的敏感度相对更大。但随着时间的推移，海水养殖面积总体上对产量增长的拉动作用在逐步减弱，而专业劳动力投入对产量的影响作用则不断增强。