基于主成分特征提取的面板数据聚类方法

戴大洋，邓光明,b

（桂林理工大学a.理学院；b.应用统计研究所，广西 桂林 541006）

0 引言

面板数据（Panel Data）具有截面数据和时间序列数据的特性，在现实数据库中比较常见。它既有截面数据个体间的差异信息，又有时间序列数据的动态信息，导致单纯的时间序列分析方法和截面数据多元统计方法不再适用于面板数据。国内外大多数面板数据的理论都是从建模的角度入手[1]，而将多元统计方法引入到面板数据中只有十几年的历史。Bonzo等[2]运用概率链接函数取代传统聚类中的距离函数来定义聚类标准，把聚类过程看成是一种优化问题，运用自适应模拟退火方法（ASA）对面板数据进行聚类，首次将多元统计方法引入到面板数据中。此后，国内掀起面板数据聚类的研究热潮。

在前人的研究中，主要都从降维层面考虑，将面板数据的三维信息通过某种技术手段降为二维信息。朱建平[3]从面板数据描述层面出发，构造面板数据相似性指标，并提出面板数据聚类的单指标聚类方法。单指标面板数据自身具有简化面板数据的效果，且单指标面板数据在现实数据库中并不多见，因此，该方法适用性较窄。李因果[4]从面板数据时序特征和截面特征出发，重新定义了样本间“绝对指标”、“增量指标”和“时序波动”的距离函数和Ward聚类算法，提出了一套较为合理的面板数据聚类算法。党耀国[5]从特征提取的角度，将每个个体在时间维度上的不同指标的统计特征进行提取，以此来降低时间维度，并将所有不同指标的动态特征全部看作截面数据的指标维度，用传统的动态聚类方法来聚类。此法对于指标提取比较全面和合理，但解决指标间具有相似特征的聚类问题就存在一些缺陷：（1）将所有不同指标时期内的统计特征看成截面数据的指标维度来聚类，存在信息重叠和未区分指标间重要性差异的问题，对聚类结果造成很大干扰。（2）在提取统计特征后采用主观赋权，人为因素过重。（3）动态聚类方法因初始聚类中心选取不同而对聚类结果造成很大影响。

本文试图在特征提取的多指标面板数据聚类方法上对上述问题做出优化和改进，提出了运用主成分分析对不同指标“绝对量”特征、“波动”特征、“偏度”特征、“峰度”特征和“趋势”特征分别进行主成分提取，对每个特征分别计算综合得分，再运用熵值法计算5个特征综合得分的权重，将赋权后的数据进行系统聚类，最后用房地产面板数据进行实证分析。

1 面板数据的格式及数字特征

1.1 单指标面板数据

单指标面板数据的数据格式可用一个二维表表示，每个元素用Xi(t)表示，其中，i表示第i个个体，t表示指标记录的时期数，Xi(t)表示个体i在t时间记录的单个指标值。单指标面板数据聚类方法目前已没有争议，都是直接将时间维度看作是截面数据的指标维度，用多元统计分析中截面数据的聚类方法来解决。

1.2 多指标面板数据

多指标面板数据是时间序列数据和截面数据的组合，不能再用简单二维表表示，严格意义上应该用三维表表示，为了容易理解，下面仍用二维表表示，如下页表1，研究总体共有N个个体，每个个体记录T期，每期有p个指标，则个体i的第j个指标在第t期的值为Xij(t)，i=1，2，...，N，j=1，2，...，p，t=1，2，...，T，该二维表与简单二维表不同，它包含时间、个体和指标这三维信息。

表1 多指标面板数据

下面将给出多指标面板数据的几个统计量，指标的特征提取将用到这些统计量。

（1）个体i的第j个指标在T时期内的均值为：

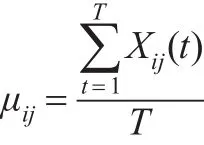
（2）个体i的第j个指标在T时期内的标准差为：

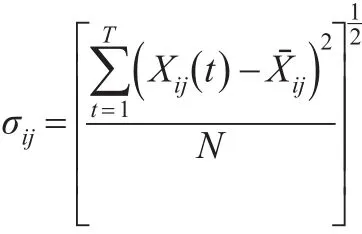
2 面板数据的特征提取

2.1 面板数据的标准化

面板数据各指标量纲或数量级不同会对聚类结果造成一定影响，故对Xij(t)进行均值化的标准化处理，标准化公式为：

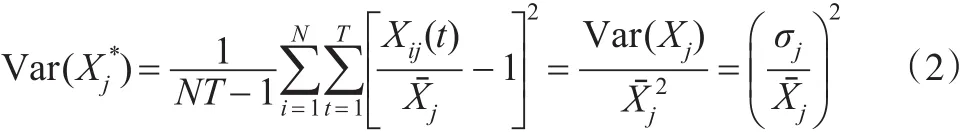
这样标准化后各指标的方差是各指标变异系数的平方，不仅消除了量纲和数量级的影响，又保留了原指标的变异信息。

2.2 面板数据指标的特征量提取

本文按照文献[5]中面板数据在时期特征量的提取思想，从指标考察期内的发展水平、趋势、波动程度、分布情况等方面对每个指标在考察期的特征量定义。对于面板数据集，设其有N个个体，每个个体记录T个时期的p项指标。

定义1：个体i的第j个指标全时“绝对量”特征，记为：

AQF(Fij)是指个体i的第j个指标在总时期T的均值，该特征量反映个体i的第j个指标在整个时期绝对发展水平。

定义2：个体i的第j个指标全时“波动”特征，记为：

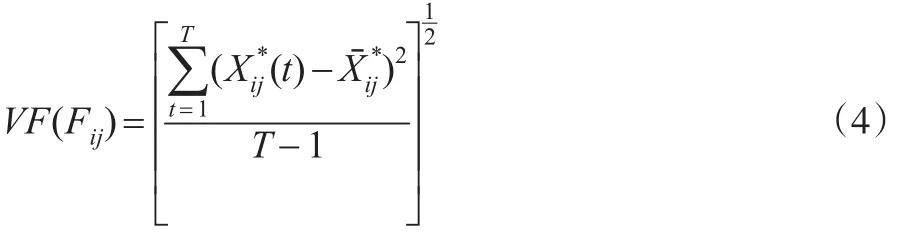
定义3：个体i的第j个指标全时“偏度”特征，记为：

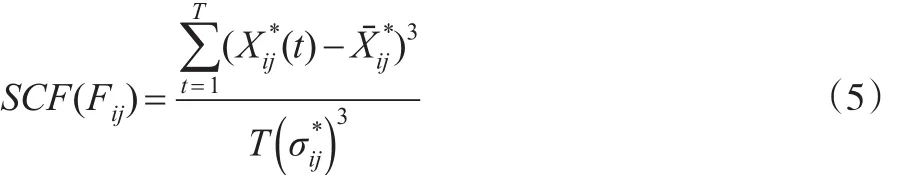
定义4：个体i的第j个指标的全时“峰度”特征，记为：

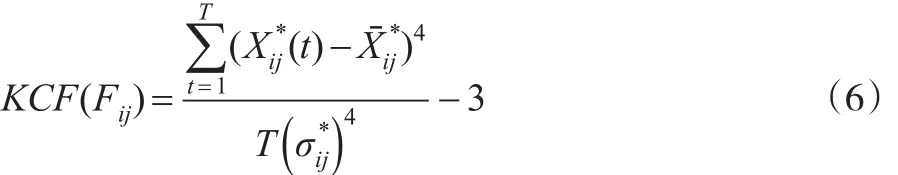
该特征量反映个体i的第j个指标在整个时期分布曲线的尖峭程度；KCF(Fij)小于0，表示该指标值的分布比正态分布更分散，KCF(Fij)小于0，表示该指标值的分布比正态分布更集中在平均值周围。

定义5：个体i的第j个指标全时“趋势”特征，记为：

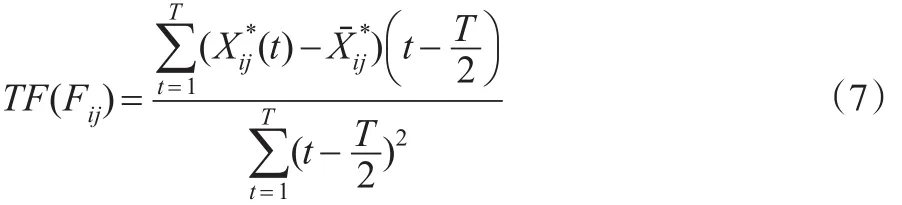
TF(Fij)描述了指标的长期变化趋势，若指标的TF(Fij)值越接近，说明这两指标都呈同坡度变化，两指标越相似。以第i个个体的第j个指标T时期的指标列为样本，建立的回归模型，利用最小二乘法估计参数β，此时的β就是TF(Fij)。

2.3 特征量的二次提取

文献[5]在提取面板数据整个时期5个方面的特征量后，分别对每个指标的各个特征量主观赋权后直接用动态聚类算法聚类出结果。但在提取每个指标相同特征统计量时，它们之间可能具有相关性。即使个体的每个指标间不具相关性，但所有指标在“绝对量”、“波动”、“偏度”、“峰度”和“趋势”的每一个特征上却可能具有相关性。在宏观经济数据中不同指标在同一时期极易存在相同的趋势或类似的波动等，若利用此时的数据集聚类，将会对聚类结果造成严重干扰。本文将对不同指标的相同特征量分别进行主成分分析，得到每个特征的综合得分。

定义6：F1，F2，…，Fp为p维指标向量AQF(Fi)=(AQF(Fi1)，AQF(Fi2)，…，AQF(Fip))提取的主成分，记αk(k=1，2，...，p)为主成分Fk的方差贡献率，则主成分降维后“绝对量”特征AQF(Fij)的综合得分为：

同理可分别定义“波动”特征、“偏度”特征、“峰度”特征和“趋势”特征的综合得分为

经前人的实验得知，取不同主成分个数时，聚类结果会全然不同，当取到全部主成分时，聚类结果趋于稳定，并达到最佳效果。为了避免数据集各变量相关度不高的情况下取（累计贡献率≥85%）前几个主成分计算综合得分时信息损失严重和聚类效果不好，此处取所有主成分，即。为了叙述方便，后面将F_AQF(Fi)、F_VF(Fi)、F_SCF(Fi)、F_KCF(Fi)、F_TF(Fi)分别称为主成分“绝对量”特征、主成分“波动”特征、主成分“偏度”特征、主成分“峰度”特征和主成分“趋势”特征。

2.4 特征量的赋权

本文中主成分“绝对量”特征、主成分“波动”特征、主成分“偏度”特征、主成分“峰度”特征和主成分“趋势”特征对个体差异影响程度会有所不同，根据它们的影响程度必须赋予相应权重wj（j=1，2，...，5），为了避免主观臆测，本文采取熵值法客观赋权[6]。

熵值法赋权的基本步骤：

（1）选取N个个体的5项指标F_AQF(Fi)、F_VF(Fi)、F_SCF(Fi)、F_KCF(Fi)、F_TF(Fi)的数据集{Zij}，则Zij为第i个个体第j个指标的数值 (i=1，2，...，N，j=1，2，...，5)；

（2）指标归一化：异质指标同质化

采用不同的算法进行标准化处理。令Zij=| |Zij，方法如下：

正向指标：

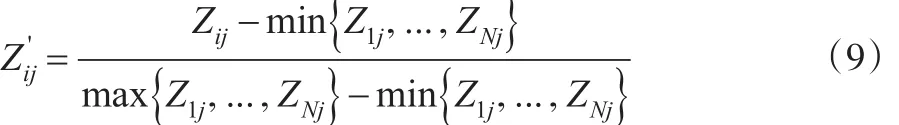
负向指标：

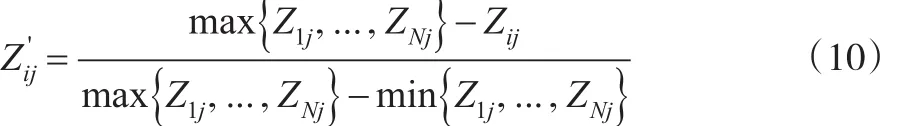
则Z'ij为第i个个体第j个指标归一化的数值，为了叙述方便，归一化的数值仍记作Zij；

（3）计算第j个指标的第i个个体占该指标的比重pij和第j个指标的熵值ej：

其中，k=1/ln(N)＞0，需满足ej≥0。

（4）计算信息熵冗余度dj和各项指标的权重wj：

编写MATLAB程序代码实现上述算法，可得出主成分“绝对量”特征、主成分“波动”特征、主成分“偏度”特征、主成分“峰度”特征和主成分“趋势”特征相应的权重

3 面板数据的聚类方法

上文从特征提取的角度减少了面板数据的时间维度，将面板数据转化为截面数据，因此，可以直接用截面数据聚类方法对面板数据进行聚类。

动态聚类算法因初始聚类中心选取不同而对聚类结果造成很大影响，不同于文献[5],考虑到聚类效果的稳定性，这里采用系统聚类[7]对面板数据进行聚类。先对N个个体的5项指标F_AQF(Fi)、F_VF(Fi)、F_SCF(Fi)、F_KCF(Fi)、F_TF(Fi)在总体上进行Z-Score标准化，以消除数量级影响，标准化后5个指标值分别记为F*_AQF(Fi)、F*_VF(Fi)、F*_SCF(Fi)、F*_KCF(Fi)、F*_TF(Fi)。然后再用数据集{w1F*_AQF(Fi)、w2F*_VF(Fi)、w3F*_SCF(Fi)、w4F*_KCF(Fi)、w5F*_TF(Fi)(i=1，2，...，N)}进行系统聚类。

4 方法应用实例

4.1 数据的来源和指标选取

本文选取房屋平均价格、国内生产总值、年末人口数、房地产开发投资额、房地产开发竣工面积、在岗职工平均工资和社会商品零售总额这5个指标[8]来反映我国房价的综合趋势水平。年末人口数和在岗职工平均工资从需求层面影响房价，房地产开发投资额和房地产开发竣工面积从供给层面影响房价，国内生产总值和社会商品零售总额从宏观经济层面影响房价，且基本都是正向影响，这些影响因素和房屋平均价格都反映房价的综合趋势水平。本文所使用的数据来源于国家统计局官网（2006—2015年）。

4.2 聚类分析

按照本文提出的面板数据聚类方法，使用SPSS20.0、MATLAB和EXCEL2007软件对我国35个大中型城市的房地产相关数据进行聚类。利用MATLAB运行熵值法算法程序计算所提取特征的权重，“绝对量”特征、“波动”特征、“偏度”特征、“峰度”特征和“趋势”特征的权重分别为0.241，0.384，0.099 ，0.144，0.132；从权重的客观赋值情况看出，时期的“绝对量”水平和“波动”水平对个体间差异的贡献程度都比较大，“偏度”、“峰度”和“趋势”水平的贡献程度相对而言比较小，可以理解为这些年的数据整体上都有一个大的增长趋势，导致“偏度”、“峰度”和“趋势”对个体差异影响不大，所以熵值法计算的权重有一定的合理性。

将本文面板数据的聚类方法用EXCEL2007和SPSS20.0软件实现，根据软件输出结果作出聚合系数随分类数变化的曲线图（如图1），从图1可以看出，当分类数为5时，曲线变的比较平缓，于是把分类数确定为5，从而得出房价的综合趋势水平的聚类结果（如表2）。

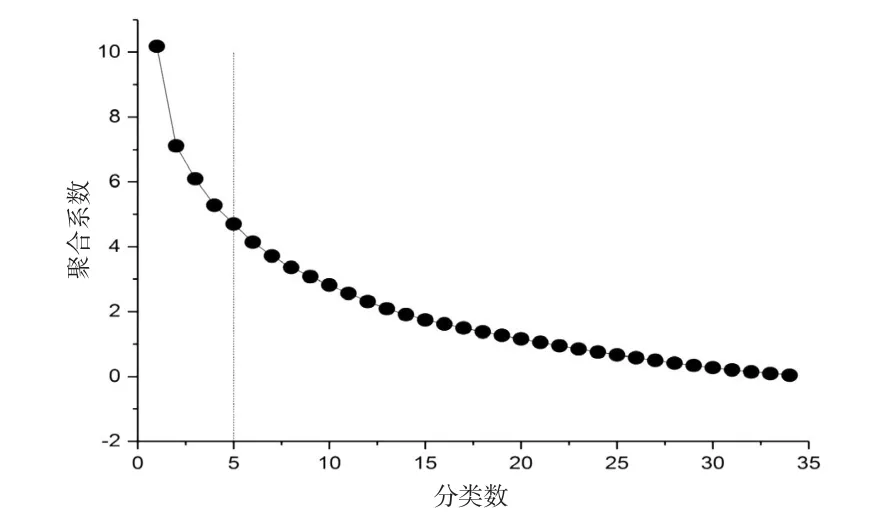
图1 聚合系数随分类数的变化

表2 新方法下房价综合趋势水平的面板数据聚类结果

第一类包括北京，上海，这些城市发展较早，又是中国的政治文化中心和金融中心，房地产业繁荣，属于房价综合趋势水平最高的城市；第二类包括天津，杭州，广州，深圳，这些城市是中国的重要港口和沿海城市，对外贸易最活跃，房地产业相对比较发达，属于房价综合趋势水平较高的城市；第三类包括石家庄，太原，呼和浩特，沈阳，大连，长春，哈尔滨，南京，宁波，合肥，福州，厦门，南昌，济南，青岛，武汉，长沙，南宁，海口，成都，贵阳，昆明，西安，兰州，西宁，银川，乌鲁木齐，这些城市属于房价综合趋势水平一般的城市；第四类包括郑州，郑州独自成为一类，属于房价综合趋势水平较低的城市；第五类包括重庆，重庆是有名的山城雾都，房地产比较萧条，属于房价趋势水平最低的城市。

从聚类结果发现，改进后的面板数据聚类方法很好的将大中型城市房价的综合趋势水平进行一个合理划分，划分的结果使得每类都比较符合实际情况。若未消除相同特征间的重叠信息，采用文献[5]中方法进行聚类，聚类结果（如表3）将多数成员聚为一类，其余个体单独成类，聚类效果极差，与实际情况不符。可以看出，对指标间具有相似特征的这类面板数据，原方法近乎失效，改进后的面板数据聚类方法效果显著。

表3 未改进的面板聚类方法的聚类结果

5 结论

本文提出的聚类方法适用于少量缺失数据的多指标面板数据的样本分类问题，该方法综合考虑了面板数据时间维度上的“绝对量”特征、“波动”特征、“偏度”特征、“峰度”特征、“趋势”特征等5个动态特征，消除了每个特征上的信息重叠，利用熵值法解决了这些特征的权重问题。最后利用该方法对2006—2015年我国大中型城市房价相关数据进行了实证分析，结果表明新方法能较好的解决指标间具有相似特征的多指标面板数据聚类问题。