灰色面板数据的关联决策评价模型拓展

蒋诗泉，刘思峰，刘中侠，谢乃明

（1.铜陵学院 数学与计算机学院，安徽 铜陵 244000；2.南京航空航天大学 经济与管理学院，南京 210016）

0 引言

灰色关联分析是一种因素分析方法，且对样本量的多少和有无规律都能够适应，其基本思想是根据序列曲线几何形状的相似程度来判断不同序列之间的联系是否紧密[1]。国内外学者在关联度模型方面研究成果丰富，比如：B型、C 型关联度[2，3]、T型关联度、斜率关联度[4]、凸关联度[5]、面积关联度[6]、广义关联度[7]、相似性和接近性灰色关联模型[8]、多维空间关系的关联度模型[8,9]。文献[10,11]将向量空间的关联度模型拓展到矩阵空间，进而提出了基于面板数据的灰色关联度模型及其性质。对于面板数据的关联模型度研究很少，且多以凹凸性等视角进行刻画此关联关系，但是这对较为分散的面板数据往往很难准确刻画整体发展趋势[12]。对于面板数据类型为一般灰数的关联模型研究极其稀少，文献[13-15]仅研究了决策信息为区间灰数的一般关联决策模型。在实际决策问题中，可能会造成决策信息表现为复杂性和不确定性，而目前对不确定信息表征和运算不够完善。为更加准确地表征不确定信息，本文首先给出了一般灰数的概念并用一般灰数表征复杂信息和不确定性、一般灰数的距离测度方法及其运算法则；其次，将灰色面板数据转化为时间关于样本在指标上值的时间矩阵序列；最后，基于关联度构造思想，构建灰色面板数据的灰色关联度模型并应用于动态多指标综合评价。

1 灰色面板数据关联度模型的理论基础

1.1 一般灰数的相关理论

定义1[1]：设，则称g±为一般灰数。其中任一区间灰数，满足且分别称为g±的下界和上界，其中区间灰数和实数是一般灰数的特例。

定义2[1]：（1）设为一般灰数，称为g±的核。（2）设g±为概率分布已知的一般灰数，的概率为pi且满足pi＞0 ，，则称为g±的核。

定义3[1]：设一般灰数的背景或论域为为 Ω 的测度，则称为一般灰数g±的灰度。一般灰数g±的灰度亦简记为gο。其中，记为 ⊗i的灰度，且

定理1：设R(g±)为一般灰数构成的集合，一般灰数g1±和g2±之间的距离满足三个条件：

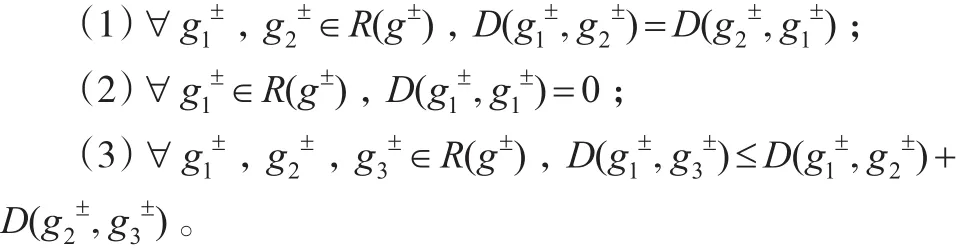
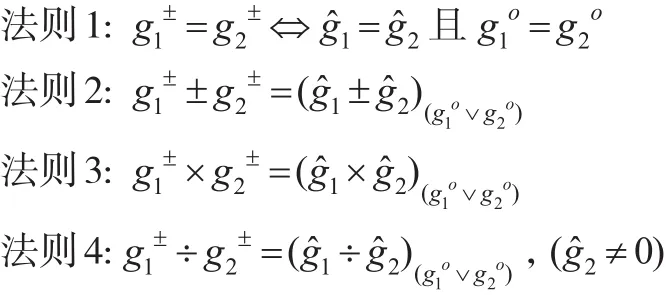
1.2 灰色面板数据的矩阵表示

灰色面板数据结构比较复杂，它的横向是截面数据，纵剖面是时间序列。设有N个样本，每个样本有M个指标，观测时间长度为T，那么可以将面板数据转化为一个二级二维表的形式[13]，为了便于编程计算，将灰色面板数据用矩阵表示，具体见定义5。

定义5：设有N个样本，每个样本有M个指标，观测时间长度为T，灰色面板数据X(⊗)中第t时刻关于样本i在指标m的值记为gt±(i，m)＞0 ，其中i=1，2，…，N，m=1，2，…，M，t=1，2，…，T。则称为t时刻的样本指标观测矩阵。那么对应的灰色面板矩阵序列X(⊗)=(X1(⊗)，X2(⊗)，…，XT(⊗))称为时间矩阵序列。

类似于定义5可以定义样本矩阵序列及指标矩阵序列，由于这三个序列没有主次之分，只是角度不同而已，且关联度模型的构造机理极其相似，故本文以时间矩阵序列为例研究灰色面板数据的关联度模型。

2 灰色矩阵数据规范化算子

在决策评价过程中为了消除指标量纲和量级的影响以及使其具有可比性，首先要对指标进行规范化处理。设第t个时刻关于样本i在指标m的值记为，其中t=1，2，…，T。

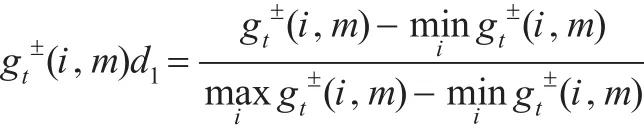
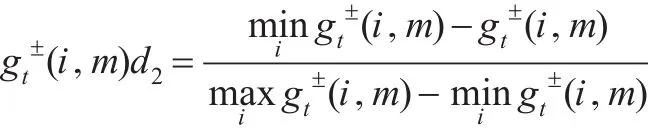
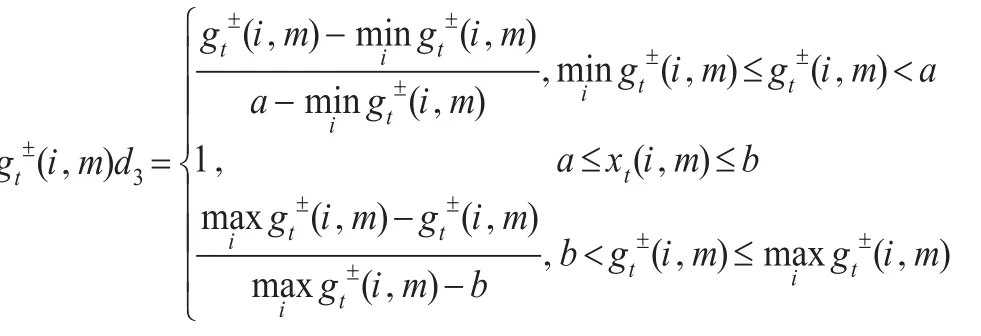
3 灰色面板数据的关联度模型构建

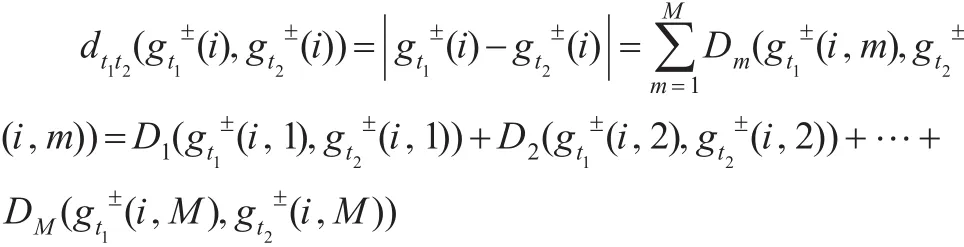
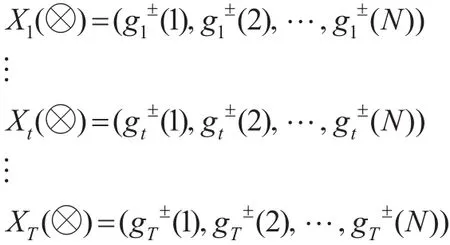
对于ξ∈(0，1)令：

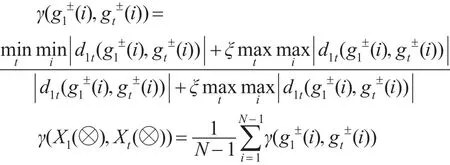
称γ(X1(⊗)，Xt(⊗))为基于时间的灰色面板数据关联度。

可以证明该关联度满足：

类似地，可以定义基于样本的灰色面板数据关联度模型、基于指标的灰色面板数据关联度模型。

4 基于灰色面板数据的关联度决策算法步骤

步骤1:灰色面板数据规范化预处理。

步骤2:确定正、负理想样本矩阵。

gt±(i，m)为第t个时刻关于样本i在指标m的值规范化后记为rkji，则t时刻正、负理想为:

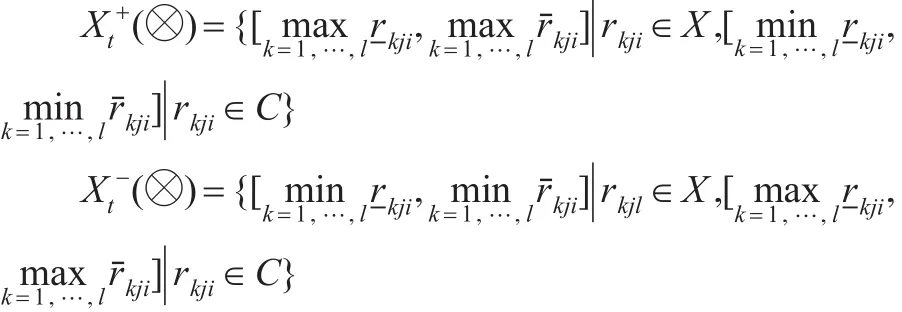
其中X,C分别表示效益型指标和成本性指标。

步骤3：将规范化决策评价矩阵表示为简化形式的灰色决策矩阵。

步骤4：分别计算与正、负理想矩阵的关联度值。

步骤5：计算相对贴近度并进行排序。

5 案例分析

设有三家企业A1，A2，A3，评价指标为S1：表示企业年产值（千万元），S2:表示企业社会效益（千万元），S3：表示对环境效率，三个时间样本点分别为2012—2014年。考虑篇幅限制，将灰色面板数据转化为三个时间序列决策矩阵如下，对三家企业进行综合评价。

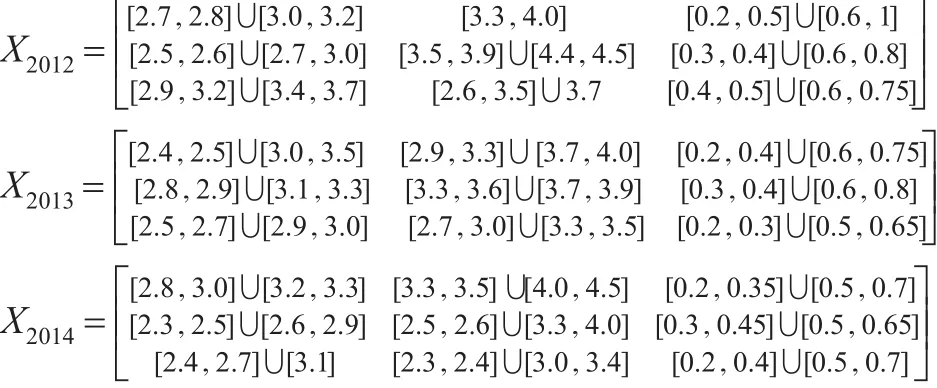
步骤1:将决策矩阵进行规范化处理。

步骤2:确定正、负理想样本时间矩阵。

步骤3:将规范化矩阵表示为简化形式的矩阵。

步骤4：计算正理想方案与各样本的关联度。分别计算正理想与各样本之间的距离d+i(m)、关联系数和关联度γ+i。

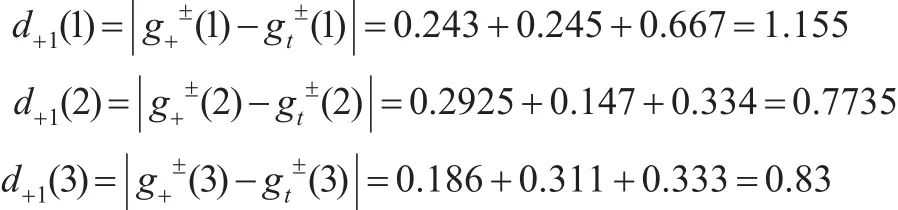
类似可以计算，d+2(1)=1.206，d+2(2)=0.605，d+2(3)=0.9945。d+3(1)=1.003，d+3(2)=0.998，d+3(3)=1.31。

根据定理2计算正理想与各样本的关联系数分别为：

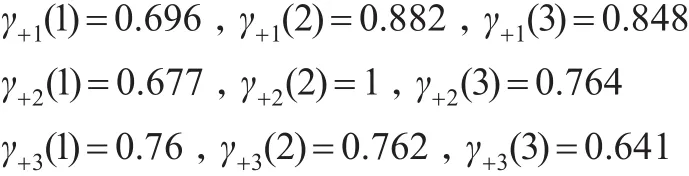
正理想与样本的关联度值分别为：γ+1=0.809，γ+2=0.814 ，γ+3=0.721。

故关联度排序为：γ+2＞γ+1＞γ+3。也即样本排序为A2≻A1≻A3。

步骤5:计算与负理想的关联度。分别计算负理想与样本之间的距离d-i(m)、关联系数γ-i(g-±(m)，gt±(m))和关联度γ-i。计算方法类似以步骤4。

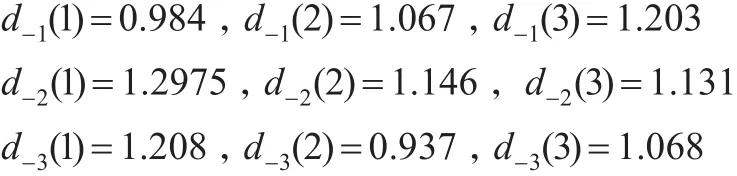
根据定理2计算负理想与样本的关联系数分别为：

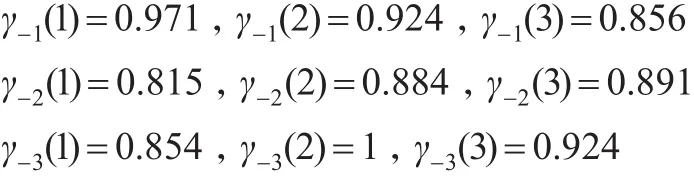
负理想与各样本的关联度值分别为：γ-1=0.917，γ-2=0.863，γ-3=0.926。

故关联度排序为：γ-3≻γ-1≻γ-2，也即样本排序为A2≻A1≻A3。

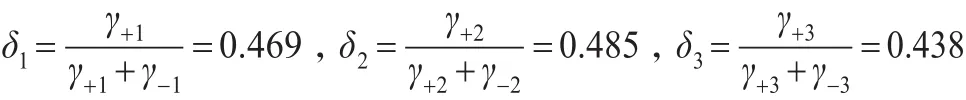
依照相对贴近度的方案排序为A2≻A1≻A3。

通过以上的结论可以看出不论是依据与正理想的关联度、与负理想的关联度还是相对贴近度的排序其结果都是完全一致的。

6 结束语

为了克服区间灰数表征复杂不确定信息的缺失，本文利用一般灰数表征复杂不确定信息，解决了决策信息不能够被充分精确表征的问题。本文基于灰色关联度构建的基本思想，将邓式关联度模型推广到灰色面板数据的情形，在此基础上构建了基于灰色面板数据的多指标动态决策评价的关联度方法，从而拓展了灰色关联分析理论的应用范围，丰富了灰色关联度理论。另外，在本文的基础上，可以进一步研究各指标权重的确定方法、n维空间的决策模型构建方法以及高维场数据的决策模型的构建方法。最后的算例也充分验证了该模型的有效性和合理性。